从以上的分析可以看出,当电阻R不同时,L×Cnorm坐标系中同一种反孤岛方案的NDZ不同,这样L×Cnorm坐标系便不能很好地反映出负载电阻的变化对反孤岛方案NDZ的形状以及大小的影响。为克服这一不足,本节定义了以负载品质因数Qf为横坐标而负载谐振频率f0为纵坐标的负载特征参数坐标系Qf×f0,并推导出以Qf和f0为参数的几种基于频率的反孤岛方案的相位判据。
7.4.3.1 Qf×f0坐标系及其孤岛检测的相位判据[14]
从式(7-41)和式(7-42)可以看出,由于负载的阻抗角φload受负载品质因数Qf和谐振频率f0的影响,并且电阻R的增加可以通过Qf的增加来反映(对给定的一组L和C),因此在以负载品质因数Qf为横坐标而负载谐振频率f0为纵坐标的Qf×f0坐标系中分析反孤岛方案的NDZ时,就无需像在L×Cnorm坐标系中分析NDZ一样因电阻R的改变而绘制新的曲线。可见Qf×f0坐标系是反孤岛方案有效性评估的一个很好的选择。
在负载特征参数坐标系Qf×f0中对反孤岛方案的NDZ进行分析时,也要用到相应的相位判据来对NDZ进行定量的描述。与L×Cnorm坐标系中孤岛检测的相位判据类似,Qf×f0坐标系中孤岛检测的相位判据为
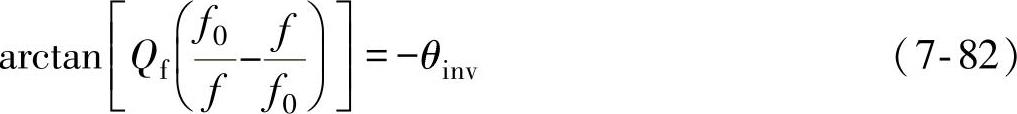
如果满足式(7-82)的频率f在频率正常工作范围内,孤岛效应将持续发生,因此可以用式(7-82)来评估Qf×f0中基于频率的反孤岛方案的有效性。
由式(7-82)可知,对负载特征参数坐标系Qf×f0中的每一点,孤岛系统的稳态频率都能用特定反孤岛方案的相位判据来计算。如果孤岛系统的稳态频率在过/欠频率阈值的范围内,那么孤岛系统中具有该品质因数和谐振频率的RLC负载的稳态工作点就位于所采用的反孤岛方案的NDZ以内,否则就位于NDZ之外。
与L×Cnorm坐标系中孤岛检测的有效性分析相同,由于并网逆变器的恒功率工作模式和恒电流工作模式对负载特征参数坐标系Qf×f0中过/欠频率保护方案的NDZ没有影响,因此无需就恒功率模式和恒电流模式分别进行讨论。
7.4.3.2 Qf×f0坐标系中孤岛检测的NDZ边界
本小节讨论了以Qf和f0为变量的几种基于频率的反孤岛方案,主要包括过/欠频率、滑模频移、主动式频移方案。利用相位判据并考虑频率的工作范围,可以得出Qf×f0坐标系中各方案的NDZ边界,从而为评估反孤岛方案的有效性打下基础。
1.过/欠频率保护方案的NDZ边界
参照图7-14,并由式(7-45)可知,电网跳闸后,逆变器输出端电压到达稳态时的频率就是负载的谐振频率f0。如果fmin≤f0≤fmax,过/欠频率反孤岛检测失败,从而无论并网逆变器工作于恒功率模式还是恒电流模式,孤岛效应都将持续发生。
2.相位跳变方案的NDZ边界
相位跳变方案的NDZ边界可用φload<φth表示,其中φth是相位跳变方案中规定的相位阈值,有:
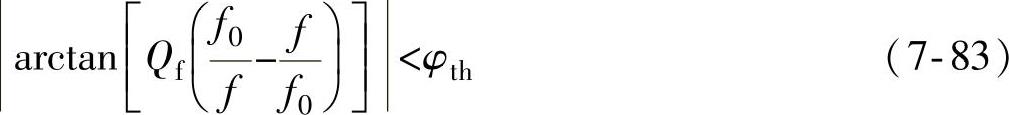
由上式可以解得负载的谐振频率f0为
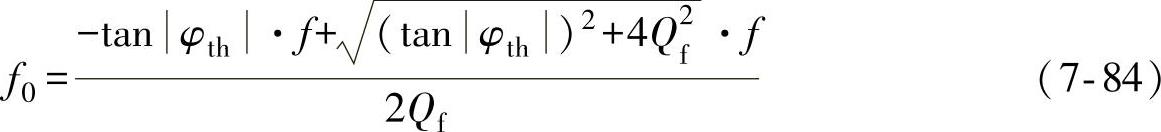
根据式(7-83),Qf×f0坐标系中相位跳变方案中的NDZ可通过分别计算f=fmax和f=fmin情况下的Qf和f0得到。考虑到:对谐振频率f0<fg的负载,逆变器输出到达稳态时的频率f<fg,而对谐振频率f0>fg的负载,逆变器输出达到稳态时的频率f>fg,因此Qf×f0坐标系中相位跳变方案的NDZ边界为
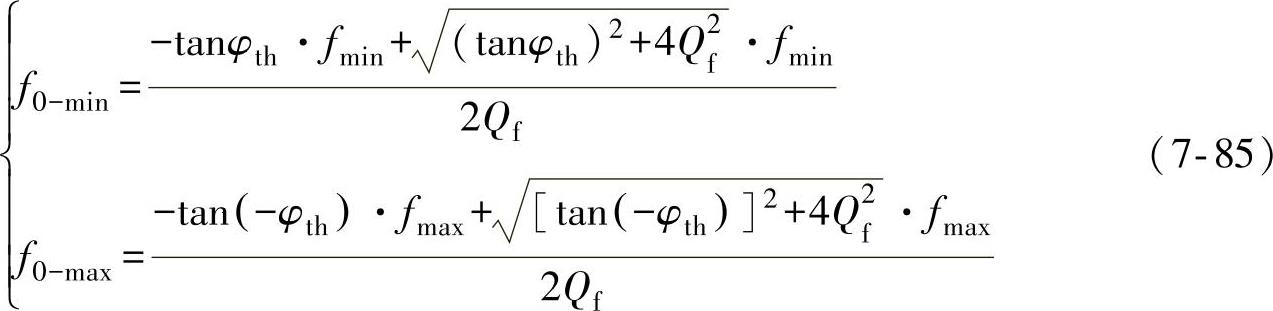
3.滑模频移方案的NDZ边界
根据7.4.2节中的相位判据φload(f)=-θSMS(f)和式(7-82)可知,Qf×f0坐标系中滑模频移方案的NDZ可以通过分别计算f=fmax和f=fmin情况下的Qf和f0得到。由于采用滑模频移方案时的逆变器输出电流与端电压之间的相位角θSMS(f)与负载阻抗角φload(f)都是f的非线性函数,因此可以利用arctanθ≈θ来简化负载阻抗角。考虑到滑模频移方案的NDZ仅存在于非常接近电网频率的频率范围内,于是可以通过某个工作点附近的微偏线性化来简化非线性函数,具体是对φload运用泰勒级数展开,并且忽略Δf的二次以及更高次项,得到

式中

这样,负载阻抗角的近似线性函数为

将式(7-88)代入φload(f)=-θSMS(f),得到(https://www.xing528.com)

同理考虑到:对谐振频率f0<fg的负载,逆变器输出到达稳态时的频率f<fg,而对谐振频率f0>fg的负载,逆变器输出到达稳态时的频率f>fg,因此滑模频移方案的NDZ边界由下式确定:
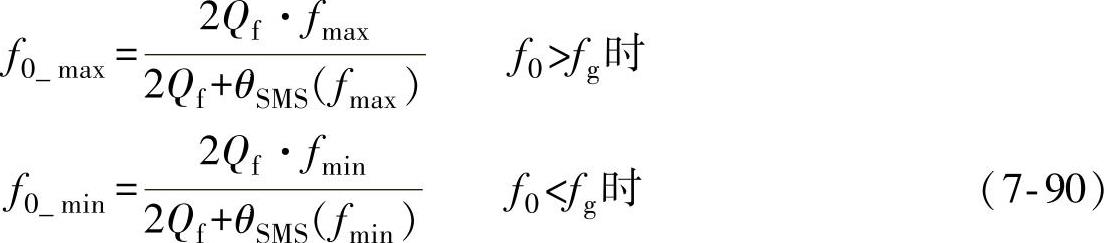
4.主动式频移方案的NDZ边界
若以向上恒频率偏移方案进行讨论,此时,并网逆变器输出电流频率总是比前一周期的电压频率高δf,即fik=fvk-1+δf。
当孤岛效应发生且系统到达稳态时,并网逆变器输出电流超前于端电压的相位角θinv可近似为
θinv=πftz=πf[1/f-1/(f+δf)] (7-91)
将式(7-91)代入式(7-82),得到主动式频移方案的相位判据为
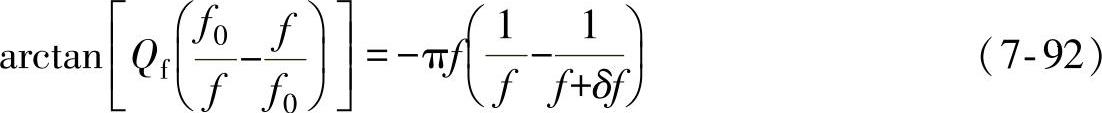
对于足够小的δf,θinv=φload趋向零,因此可利用近似等式arctanθ≈θ和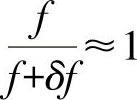 来简化式(7-92),得到
来简化式(7-92),得到

于是,孤岛系统的稳态频率可以近似表示为

由式(7-93)可以得到负载的谐振频率f0为
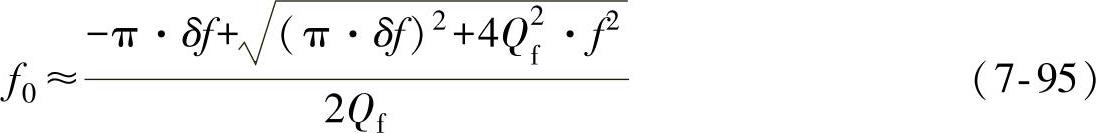
根据式(7-95),Qf×f0坐标系中主动式频移方案的NDZ可通过分别计算f=fmax和f=fmin情况下的Qf和f0得到。同理考虑到:对谐振频率f0<fg的负载,系统到达稳态时的频率f<fg,而对谐振频率f0>fg的负载,系统到达稳态时的频率f>fg,因此主动式频移方案的NDZ边界为
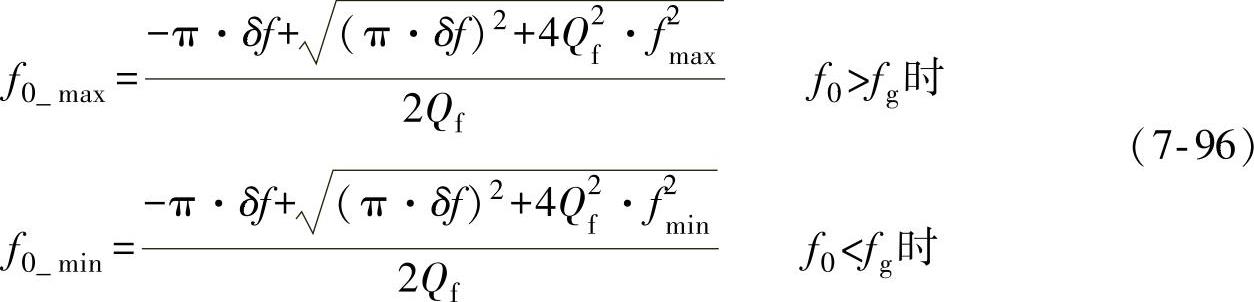
5.Sandia频移方案的NDZ边界
若采用Sandia频移方案(即带正反馈的主动频移式反孤岛检测—AFDPF),其控制策略中的斩波因子为cf=cf0+kΔf,其中Δf=f-fg,为电网跳闸后逆变器输出端电压频率与电网额定频率之差,由前面的分析可以得到Sandia频移的相位判据如下式:
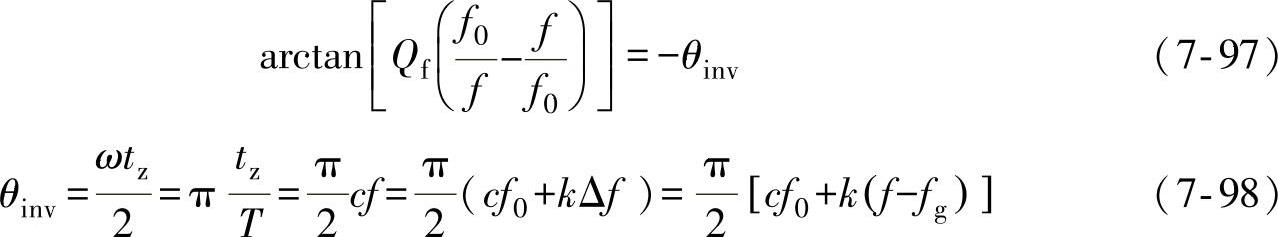
并且由式(7-97)可以解得负载的谐振频率f0为
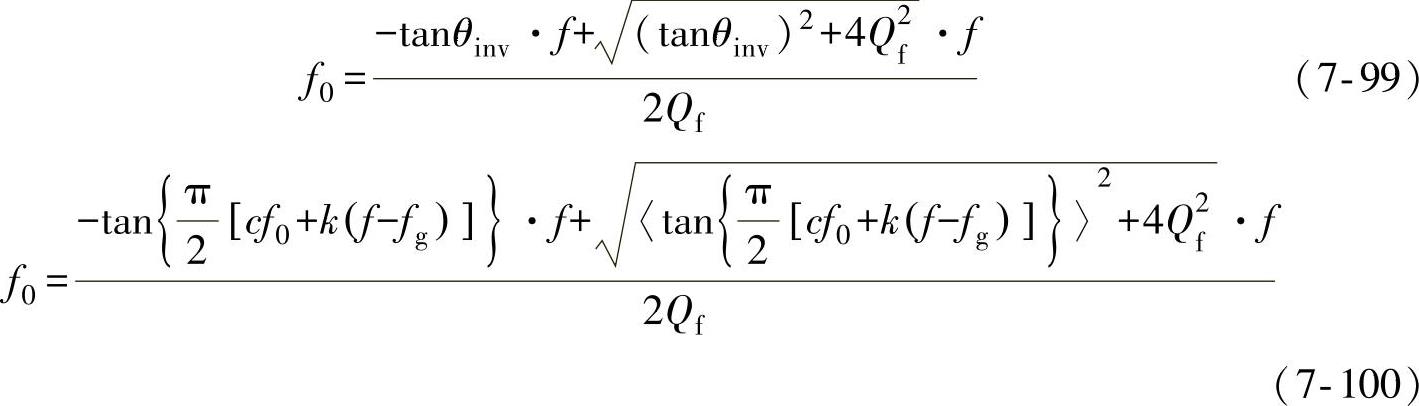
根据式(7-100),Qf×f0坐标系中Sandia频移方案的NDZ可通过分别计算f=fmax和f=fmin情况下的Qf和f0得到。同理考虑到:对谐振频率f0<fg的负载,系统到达稳态时的频率f<fg,而对谐振频率f0>fg的负载,系统到达稳态时的频率f>fg,因
此Sandia频移方案的NDZ边界为
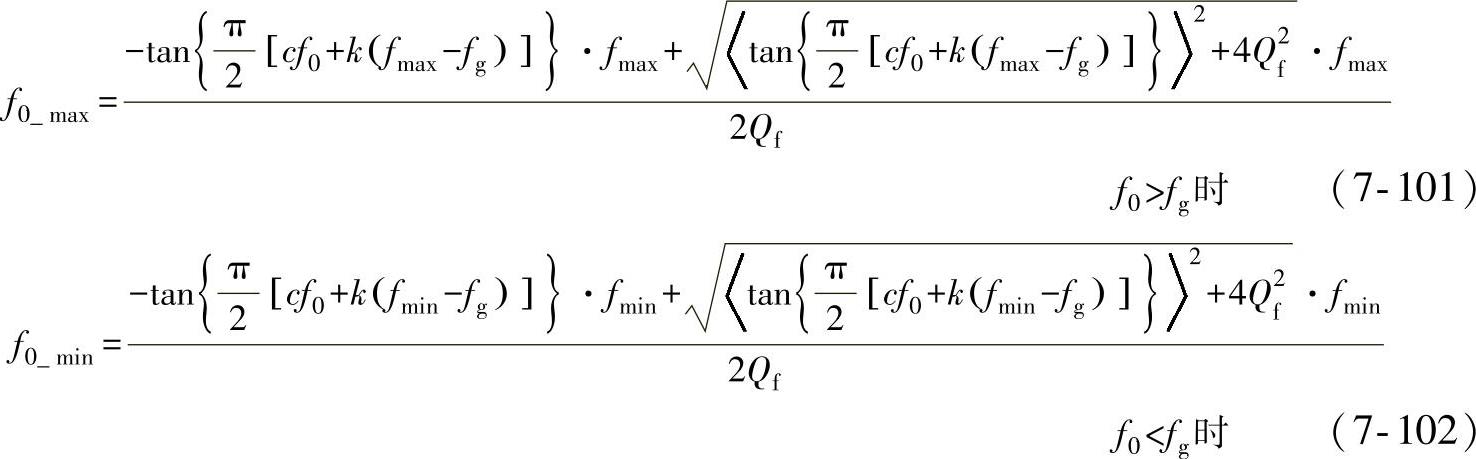
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




