基于L×Cnorm坐标系的孤岛检测有效性评估

在功率不匹配ΔP和ΔQ较小时，过/欠电压和过/欠频率孤岛检测方案将检测失败。虽然通过减小电压和频率的工作范围可以减小NDZ，但是这样会导致误跳闸。许多主动式反孤岛方案通过向系统引入扰动以使系统的工作点偏离正常范围，从而可以减小孤岛检测的NDZ以提供更好的孤岛检测性能，然而，由于功率不匹配坐标系ΔP×ΔQ不能用来评估主动式反孤岛策略的有效性，因此需要一种基于具体负载参数的坐标系以准确评估主动式反孤岛策略的有效性。本节定义了以负载电感L为横坐标而以负载“标准化电容”C_norm为纵坐标的负载参数坐标系L×C_norm，“标准化电容”C_norm考虑了负载谐振频率等于电网频率时的最不利孤岛检测因素，因而可以针对最不利孤岛检测情况的负载进行分析。另外，在负载参数坐标系L×C_norm基础上，推导出以R、L和C为变量的几种基于频率的反孤岛策略的相位判据。

7.4.2.1L×C_norm坐标系及其孤岛检测的相位判据

相位判据是用来分析基于频率变化的反孤岛策略有效性的一项指标。由于触发过/欠电压保护需要较大的有功功率不匹配，且系统中电压变动比频率变动相对难实现，所以许多主动式反孤岛方案都采用偏移频率来触发过/欠频率保护的方法，因此对基于频率的反孤岛方案有效性的研究是有意义的。

由于负载参数坐标系L×C_norm中反孤岛策略的NDZ与其对应的相位判据密切相关，因此必须弄清相位判据的含义。考虑图7-13所示的原理电路，并参阅前面章节中的孤岛效应发生机理可知：孤岛效应的发生必须满足相位平衡关系，即φ_load+θ_inv=0，其中θ_inv是由所采用的反孤岛方案决定的并网逆变器输出电流超前于逆变器输出端电压的相位角，φ_load是负载阻抗角。由于这种相位平衡关系是孤岛效应发生的必要条件之一，因此φ_load+θ_inv=0可作为孤岛效应发生的一个判断标准，简称为相位判据。

在RLC负载的情况下，相位判据可用具体负载参数（即R、L和C）和频率ω的表达式来描述，即

arctan[R（（ωL）-1-ωC）]=-θ_inv （7-62）

式中，ω是电压u_a的频率，R、L和C分别为负载的电阻、电感和电容值。

如果满足式（7-62）的ω在频率正常工作范围内，孤岛效应将持续发生，因此可用式（7-62）来评估基于频率的反孤岛方案的有效性。

采用相位判据，可以在以负载电感L为横坐标而以负载“标准化电容”C_norm为纵坐标的负载参数坐标系L×C_norm中描绘出基于频率的反孤岛方案的NDZ。

为研究负载谐振频率等于电网频率时的孤岛检测最不利情况，“标准化电容”C_norm定义为负载电容C与谐振电容C_res之比，定义谐振频率C_res使其与负载电感L的谐振频率等于电网频率ω_g，即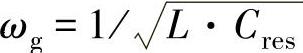：，于是C_norm可以用负载电感L的函数式表示

C_norm=C/Cres=Cω²_gL （7-63）

将式（7-63）代入式（7-62），得到

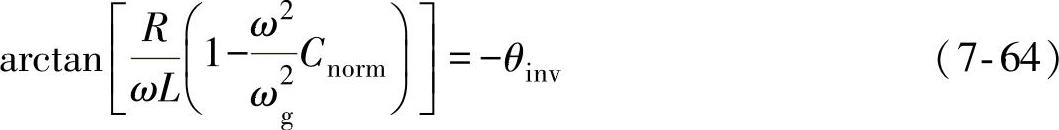
式（7-64）可称为L×C_norm坐标系中孤岛发生的相位判据。由式（7-64）可知：对负载参数坐标系L×C_norm中的每一点，孤岛系统的稳态频率都能用特定反孤岛方案的相位判据来计算。如果孤岛系统的稳态频率在过/欠频率阈值范围内，那么孤岛系统中的RLC负载的稳态工作点就位于所采用的反孤岛方案的NDZ以内，否则就位于NDZ之外。值得注意的是：相位判据只能预测基于频率的反孤岛方案NDZ的大小和位置，而不能预测孤岛效应持续发生的时间。

此外，与在ΔP×ΔQ坐标系中过/欠频率孤岛检测NDZ的分析不同，并网逆变器的恒功率工作模式和恒电流工作模式对负载参数坐标系L×C_norm中过/欠频保护的NDZ没有影响，所以无需就恒功率模式和恒电流模式分别进行讨论。

7.4.2.2 L×C_norm坐标系中孤岛检测的NDZ边界

本小节讨论了以R、L和C为变量的几种基于频率的反孤岛策略的相位判据，包括过/欠频率保护、相位跳变、滑模频移、主动式频移以及sandia频移方案。利用相位判据，并考虑频率的工作范围，可以得出L×C_norm坐标系中各方案的NDZ边界，根据NDZ的大小就可以评估反孤岛方案的有效性。

1.过/欠频率孤岛检测的NDZ边界

若考虑并网逆变器的单位功率因数运行，即θ_inv=0，由式（7-64）易得L×C_norm坐标系中过/欠频率孤岛检测的相位判据为

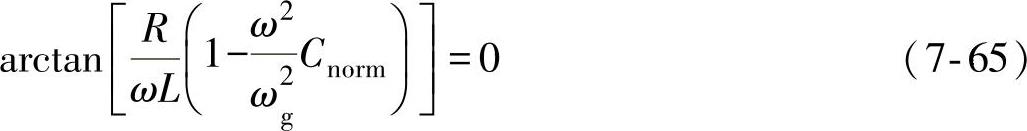
上式可以等效为

以上推导表明：孤岛发生后，系统中的频率会持续变化直到式（7-66）成立，而满足式（7-66）的频率就是负载的谐振频率ω₀（ω₀=1/LC）。在谐振频率ω₀处，系统频率到达稳态，如果此时ω₀超出了频率正常工作范围，反孤岛保护动作，孤岛效应将不会持续发生。

根据式（7-66），L×C_norm坐标系中过/欠频率孤岛检测的NDZ边界可以通过分别计算ω=2πf_max和ω=2πf_min情况下的L和C_norm而得到，即

式中 f_g——电网频率。

2.相位跳变孤岛检测的NDZ边界

类似过/欠频率孤岛检测的NDZ分析，相位跳变孤岛检测的相位判据如下

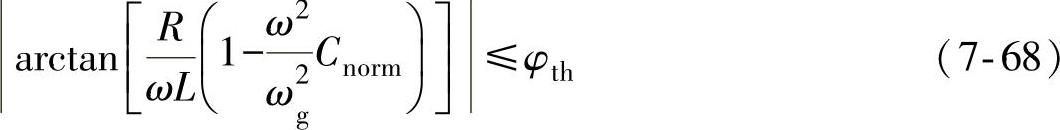
式中 φ_th——相位跳变孤岛检测中规定的相位阈值。

可见，负载阻抗角φ_load（f）是频率f的非线性函数，当逆变器单位功率因数运行时，由于θ足够小，因而可利用arctanθ≈θ对式（7-68）进行微偏线性化，这样相位跳变孤岛检测的NDZ边界为

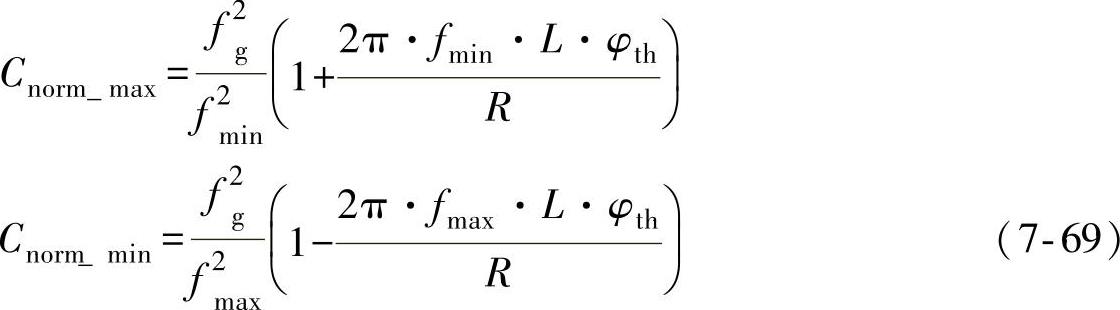
3.滑模频移孤岛检测的NDZ边界

滑模频移是对并网逆变器输出电流-电压的相位运用正反馈使得其相位偏移进而使得频率发生偏移的孤岛检测方案。当电网连接时，电网提供固定的相位和频率参考使工作点稳定在电网频率处；而当电网跳闸后，负载和并网逆变器的相位-频率工作点为负载阻抗角与并网逆变器相位响应曲线的交点，即φ_load（f）=-θ_SMS（f），其中θ_SMS是滑模频移方案中定义的并网逆变器输出电流超前于逆变器输出端电压的相位角，因此滑模频移孤岛检测的相位判据为

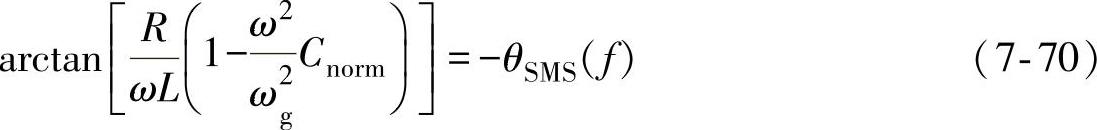
同理可利用arctanθ≈θ对式（7-70）进行微偏线性化，考虑频率工作范围为f_min≤f_a≤f_max，于是滑模频移方案的NDZ边界由下式确定(www.xing528.com)

4.主动式频移方案的NDZ边界

前面的分析已知，当孤岛系统中的负载是容性的情况下，孤岛系统的频率有下降趋势。如果系统采用向上频移的主动式频移反孤岛策略，那么孤岛发生后，容性负载所导致的频率下降趋势将抑制或抵消并网逆变器向上主动频移的趋势，从而使孤岛效应能够持续进行。换言之，对RC或RLC负载的并网系统，主动式频移方案必然存在NDZ。

采用恒频率偏移（即δf不变）的并网逆变器的输出电流可由下式表示

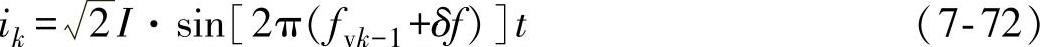
因此，采用恒频率偏移的并网逆变器输出电流的基波分量超前于逆变器输出端电压的相位角θ_inv可近似表示为

θ_inv=0.5ωt_z （7-73）

式中 t_z——主动式频移反孤岛策略中正弦波电流中插入的死区时间。

由于t_z=1/f_v-1/f_i≈1/f-1/（f+δf），于是式（7-73）可化为

θ_inv=πft_z=πf[1/f-1/（f+δf）] （7-74）

将式（7-74）代入式（7-64），得到主动式频移方案的相位判据为

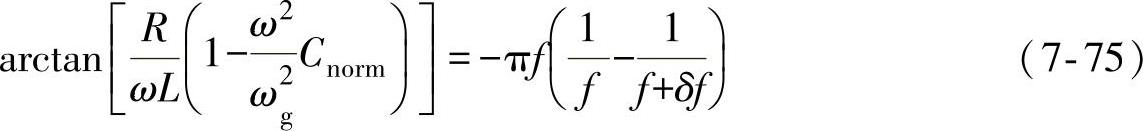
一方面，小的δf取值使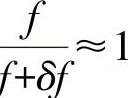，由此简化式（7-75），得到

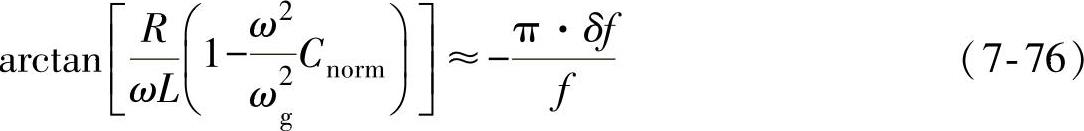
另一方面，由于θ_inv=φ_load很小，即arctanθ≈θ，代入式（7-75）可得到孤岛系统的稳态频率的近似表达式为

一旦孤岛系统到达式（7-77）确定的且比负载谐振频率略高的稳态频率时，系统的频率将不再升高。如果这一稳态频率在逆变器过/欠频率阈值范围内，并且RLC负载的电压幅值也在逆变器过/欠电压阈值范围内时，孤岛效应将持续进行。

根据式（7-76），L×C_norm坐标系中主动式频移孤岛检测的NDZ边界可以通过分别计算ω=2πf_max和ω=2πf_min情况下的L和C_norm得到，即

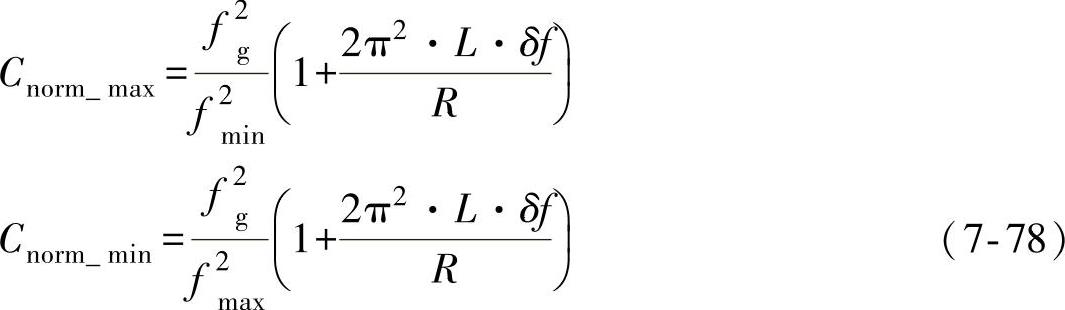
5.Sandia频移方案的NDZ边界

Sandia频移是带正反馈的主动式频移，其斩波因子cf在每个周期都会发生变化，即

cf_k=cf_k-1+K·Δω_k （7-79）

式中 cf_k——第k周期的斩波因子；

cf_k-1——第k-1周期的斩波因子；

K——不改变方向的加速增益；

Δω_k——第k周期电压u_a的采样频率ω_k与电网频率ω_g之间的偏差，即Δω_k=ω_k-ω_g。

当采用向上频移的Sandia频移反孤岛策略时，并网逆变器输出电流超前于端电压的相位角θ_inv=0.5ωt_z=0.5πcf，因此Sandia频移方案的相位判据为

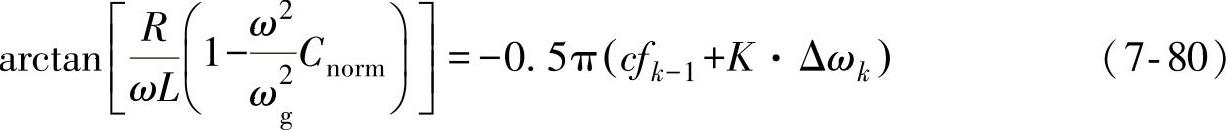
这一相位关系表明：当频率偏差增加时，孤岛效应能够持续发生，所要求的负载阻抗角也应增加，因此要到达稳态，必须使频率偏离负载的谐振频率，这就使得采用Sandia频移反孤岛策略时系统所达到的稳态频率要比采用主动式频移反孤岛策略时系统所达到的稳态频率大，从而增加了触发过/欠频率保护的可能性。Sandia频移反孤岛策略的NDZ边界可以通过分别计算ω=2πf_max和ω=2πf_min情况下的L和C_norm加以确定。

6.小结

从以上几种基于频率的反孤岛方案的相位判据可以看出：孤岛效应发生后，系统到达稳态时的频率与负载参数有关，然而有功功率及无功功率不匹配并不是由负载参数惟一决定，考虑负载需求的无功功率表达式，即

Q_load=u²_a[（ωL）^-1-ωC]=ΔQ （7-81）

式（7-81）表明：有很多L和C的组合可以得到同样的ΔQ，于是对一个给定的ΔP，这些组合都将绘制在功率不匹配坐标系中的同一点上，但是其中有些组合可能导致孤岛检测失败，而另外一些可能不会。因此在功率不匹配坐标系ΔP×ΔQ中评估反孤岛策略的有效性时，只针对特定负载而不是针对最严重情况下负载得出的NDZ可能会导致错误的结论。

总的来说，Sandia频移方案是所讨论方案中孤岛检测性能最好的一种。谐振频率等于电网频率且Q_f较大的负载将使得孤岛检测变得更困难。对于需求功率较高的负载，孤岛效应持续时间可能减少。