优化逆变器频移法检测孤岛

频移法是主动式反孤岛策略方案中最为常用的方案，主要包括主动频移（AFD）、Sandia频移以及滑模频移等主动式反孤岛策略。本节首先讨论的主动频移AFD反孤岛策略是针对过/欠频率（OFP/UFP）反孤岛策略存在较大NDZ而提出的一种主动式反孤岛策略，通过理论仿真与实验研究可以看出：AFD方案中的NDZ比过/欠频率（OFP/UFP）方案的NDZ有明显地减少。鉴于AFD方案仍然具有比较大的NDZ，因而提出了AFD方案的改进，即带正反馈的主动频移反孤岛策略，也即通常提到的Sandia频移反孤岛策略（注：Sandia国家重点实验室是美国重要的风力发电研究机构）。通过理论仿真和实验研究可知，Sandia频移方案比起AFD方案来说具有更小的NDZ，因而其检测孤岛的效率更高。但是，无论是AFD方案还是Sandia频移方案均存在稀释效应，为克服这一不足，最后讨论了无稀释效应的滑模频移反孤岛策略。

7.3.1.1 主动频移反孤岛策略—AFD方案

1.工作原理

为了克服单独使用过/欠频率OFP/UFP反孤岛策略的不足之处，研究人员首先提出了主动频移反孤岛策略—AFD方案。

AFD方案为主动式反孤岛策略方案的一种，这种主动频移反孤岛策略的原理^[25]是通过并网光伏系统向电网注入略微有点变形的电流，以形成一个连续改变频率的趋势。当连接有电网时，频率是不可能改变的。而与电网分离后，逆变器输出端电压u_a的频率被强迫向上或向下偏移，以此检测孤岛的发生。

常用执行向上频移的方案是向电网注入略微变形的电流，即在正弦波中插入死区，如图7-11所示，以一个给出的正弦波为对照，可见并网光伏系统的输出电流波形的频率被相应提高。

在前半个周期，并网光伏系统输出电流的频率略微高于电网频率，当输出电流达到零时，电流保持t_Z直到后半周期的起始点；而在后半周期，当输出电流再次达到过零点，将保持一段时间。

对于阻性负载，电压响应将跟随失真的电流波形，比纯正弦激励的响应更短的时间到过零点，如图7-11所示，当孤岛发生时，u_a的上升过零点比期望的提前到达，因此u_a和i_PV之间的相位误差增加了，这样并网光伏逆变器继续检测到频率误差并且再次增加u_a的频率，这种状况一直持续直到频率偏移足够大足以触发过/欠频率保护，从而实现主动频移反孤岛保护。

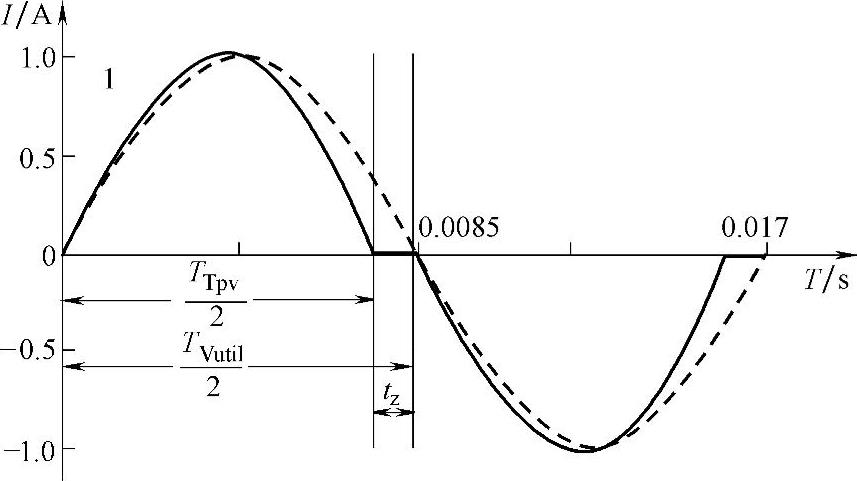
图7-11 用于AFD反孤岛方案的电流波形

但是，对于并联RLC负载，AFD可能存在不可检测区，分析如下：

不妨设负载阻抗角φ＜0，即负载呈阻容性，而负载的阻容性会导致电网跳闸时逆变器输出端的频率向下偏移，因此在孤岛发生后的第k个周期，若负载阻抗角φ的滞后作用和Δf的超前作用相抵消，且此时频率和电压未超出预设阈值，那么，系统将无法检测到孤岛的发生。同理，对于负频率偏移AFD方案且φ＞0的情况，也会存在与上述类似的问题。

2.优缺点

对基于微处理器的并网逆变器来说，主动式频移方案很容易实现；在纯阻性负载的情况下可以阻止持续的孤岛运行；与被动式反孤岛策略相比具有更小的NDZ。

但频率偏移降低了并网逆变器输出电能的质量，并且不连续的电流波形还可能导致射频干扰；为了在连接有多台并网逆变器的系统中维持反孤岛方案的有效性，必须统一不同并网逆变器的频率偏移方向，如果一些并网逆变器采用向上频移，而另一些采用向下频移，其综合效果可能相互抵消，从而产生稀释效应；并且负载的阻抗特性可能会阻止频率偏移，从而导致主动频移反孤岛策略的失效。

7.3.1.2 基于正反馈的主动频移——Sandia频移方案^[22]

综上所述，相对于被动式反孤岛策略而言，AFD方案虽然可以减小孤岛检测的盲区，但是该方法引入的电流谐波会降低并网光伏系统输出电能的质量；而在多台光伏系统并网工作的情况下，若频率偏移方向不一致，其作用会相互抵消而产生稀释效应；此外，负载的阻抗特性也可能阻止频率的偏移。因此，AFD方案仍然存在孤岛不可检测区的问题。

为了克服上述AFD方案的一些缺点，美国Sandia实验室首先提出了对该方法改进的方法——基于频率正反馈的主动频移反孤岛策略，即Sandia频移法，以下具体分析Sandia频移方案。

1.工作原理

相对电网来说，由于并网逆变器呈现出电流源的特性，即

i_inv=I_invsin（ωt+φ_inv） （7-33）

相应地，并网逆变器输出端电压u_a可表示为

u_a=U_amsin（ωt+φ_a） （7-34）(www.xing528.com)

式中，I_inv、φ_inv分别为并网逆变器输出电流i_inv的幅值和相位；U_am、φ_a分别为电压u_a的幅值和相位；ω为并网逆变器控制的频率；u_a与i_inv的相位差可用φ表示。

Sandia频移方案就是对u_a的频率ω运用正反馈的主动式频移方案。首先由图7-11定义斩波因子cf（cf=2t_z/T_Vutil），显然，cf为逆变器输出端电压频率与电网电压频率偏差的函数，即

cf_k=cf_k-1+KΔω （7-35）

其中，cf_k为第k周期的斩波因子，cf_k-1为第k-1周期的斩波因子，K为不改变方向的加速增益，Δω为u_a频率ω与电网电压频率ω_line的偏差，即Δω=ω-ω_line。

Sandia频移方案其实质是强化了频率偏差。当电网连接时，Sandia频移方案检测到微小的频率变化，并试图加快频率的变化，但是电网的稳定性禁止了频率的改变。在电网跳闸后，若频率向上偏移，则频率偏差将随u_a频率的增加而增加，斩波因子也增加，于是并网逆变器增加了输出电流的频率，这种状况持续到频率增大到触发过频保护。对于频率向下偏移的情况，u_a频率下降的情况与此类似，最终斩波因子变为负，i_inv的周期变得比u_a的长。

2.优缺点

比起AFD来说，由于正反馈的作用，Sandia频移方案将导致逆变器输出在电网跳闸后会出现更大的频率误差，这样就得到了比AFD更小的NDZ；且它兼顾考虑了检测的有效性、输出电能质量以及对整个系统暂态响应的影响。

然而由于正反馈增加了电网中的扰动，采用Sandia频移方案的并网逆变器降低了输出电能的质量，当连接到弱电网时，并网逆变器输出功率的不稳定可能导致系统不理想的暂态响应；并且当电网中并网逆变器的数量增多、发电量升高时，问题将更严重，这两种现象可以通过减小增益K来缓解，但是这将增加不可检测区域。

7.3.1.3 滑模频率偏移法

1.工作原理

主动频率偏移法是基于频率的偏移扰动，即在逆变器的输出电流中插入死区来扰动电流频率以达到孤岛检测的目的。然而这种基于频率扰动的主动频移法在多个并网逆变器运行时，会产生稀释效应而导致孤岛检测的失败。为克服这一不足，可以考虑采用基于相位偏移扰动的滑模频率偏移反孤岛策略（Slip Mode Frequency Shift）。滑模频移反孤岛方案^[15]是对并网逆变器输出电流-电压的相位运用正反馈使相位偏移进而使频率发生偏移的方案，而电网频率则不受反馈的影响。

在滑模频移反孤岛方案^[15]中，并网逆变器输出电流的相位定义为前一周期逆变器输出端电压频率f与电网频率f_g偏差的函数即

式中 f_m——最大相位偏移θ_m发生时的频率。

一般情况下控制并网逆变器工作于单位功率因数正弦波控制模式，所以并网逆变器输出电流与端电压之间相位差被控制为零。而在滑模频移方案中并网逆变器的电流-电压相位被设计成关于电压u_a的频率的函数，使得在电网频率ω_g的附近区域中并网逆变器的电流-电压相位响应曲线增加得比大多数单位功率因数负载的阻抗角的响应曲线快，如图7-12所示，这使得电网频率f_g成为一个不稳定的工作点。当电网连接时，电网提供固定的相位和频率参考使工作点稳定在电网频率f_g；而在电网跳闸后，负载与并网逆变器的相位—频率工作点成为负载阻抗角响应曲线与并网逆变器相位响应曲线的交点。

下面对图7-12中单位功率因数负载的阻抗角响应曲线进行详细分析^[22]。当电网连接时，并网逆变器的相位-频率工作点位于B点（频率为50Hz，电流-电压相位为0）。现在假定电网分离，一旦u_a的频率受到任何扰动使之偏离50Hz，并网逆变器的相位响应就将导致相位差增加，而不是下降，例如孤岛系统中的频率向上偏移时，由于滑模频移方案对相位的正反馈，并网逆变器反而加快了输出电流的频率，这就是正反馈的机理，将导致典型的不稳定。而并网逆变器在电网频率处的不稳定加强了扰动，驱使系统到达一个新的工作点，是A点还是C点由扰动的方向决定。如果并网逆变器电流-电压相位响应曲线对RLC负载来说，设计得很合适，那么A点或C点的频率将超出频率的正常工作范围，并网逆变器将停止运行。

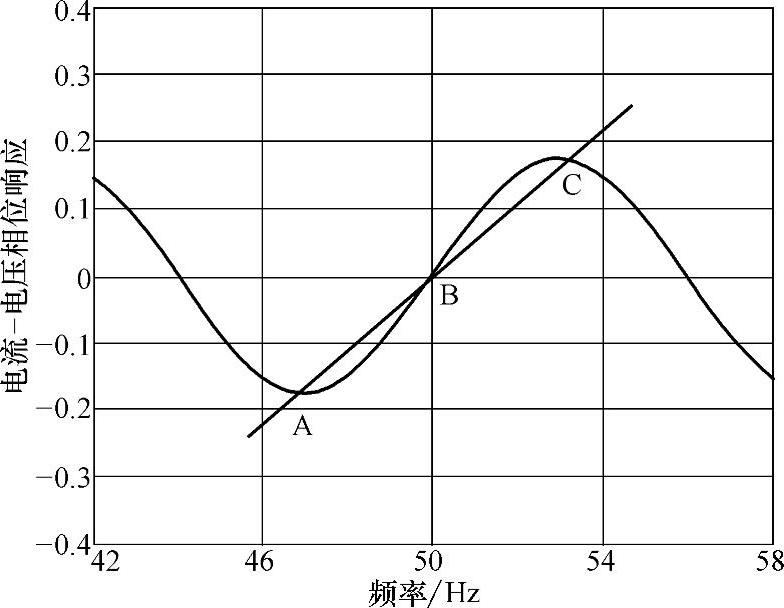
图7-12 滑模频移方案中并网逆变器输出电流-电压相位与频率间的关系

2.优缺点

与其他主动式方案相比，滑模频移方案只需要在原有的逆变器锁相环基础上稍加改动，因而易于实现；不可检测区域相对较小。在给定条件下Q_f小于额定值时可以很好地保证检测孤岛，甚至可以消除NDZ；在连接有多台并网逆变器的系统中，滑模频移方案不会产生稀释效应，效率不受多台逆变器并联影响；与Sandia频移方案一样，兼顾考虑了检测的可靠性、输出电能质量以及对整个系统暂态响应的影响。

然而由于滑模频移方案不停地对逆变器输出电流相位进行扰动，在一定程度上影响逆变电源输出电能的质量，并且在并网逆变器发电量高以及反馈环的增益大的情况下，该方案可能带来整体供电质量下降以及暂态响应等问题，这些现象在其他使用正反馈的反孤岛方案中普遍存在；在Q_f较大时滑模频移方案的孤岛检测效率降低，性能几乎接近被动式孤岛检测，并且当RLC负载的相位增加变化快于逆变器扰动的相位变化时，会导致孤岛检测失败。