如何解决局部最大功率点问题？

6.7.1.1 热斑效应^[22-26]

光伏电池是将光能转化为电能的核心环节。通常，假定同一类型的光伏电池具有完全一致的输出特性，但如果将制作过程中的误差以及随着时间而产生的老化问题都考虑在内的话，这种假设并不成立。此外，在实际应用中，不同电池板的放置的方向上可能存在倾斜角度的差别，光伏电池还有可能出现裂纹、局部遮挡、积尘覆盖等情况，导致一块或一组光伏电池的特性与整体特性不谐调，因此实际使用中，每块光伏电池的性能不可能绝对一致。当光伏电池在串、并联使用时，光伏电池输出特性的不一致将导致串、并联后的总输出功率往往小于各块光伏电池输出功率之和，这就是所谓的光伏电池的不匹配现象。当光伏电池出现不匹配情况时，其相应的失谐电池不仅对组件输出没有贡献，往往还会消耗其他电池产生的能量，形成局部过热，这种现象称为热斑效应。

通常光伏组件的结构如图6-40所示。当光伏电池串联连接，并且并联旁路二极管时，支路的短路电流约等于该支路中所有光伏电池的最小光生电流，当某块光伏电池被遮挡时，其光生电流值将出现下降，整个支路的短路电流也将随之降低，从而降低了整个回路的输出功率。如果支路输出电流大于光伏电池串联支路的短路电流时，旁路二极管将会导通，被遮挡部分的光伏电池将作为耗能器件以发热方式将该组件中其余未被遮挡光伏电池产生的部分能量消耗掉，这种能量消耗是造成热斑效应的直接原因。

以下以n块串联的光伏电池为例简要介绍热斑效应的产生过程。图6-40a所示为n块光伏电池串联的结构示意图。

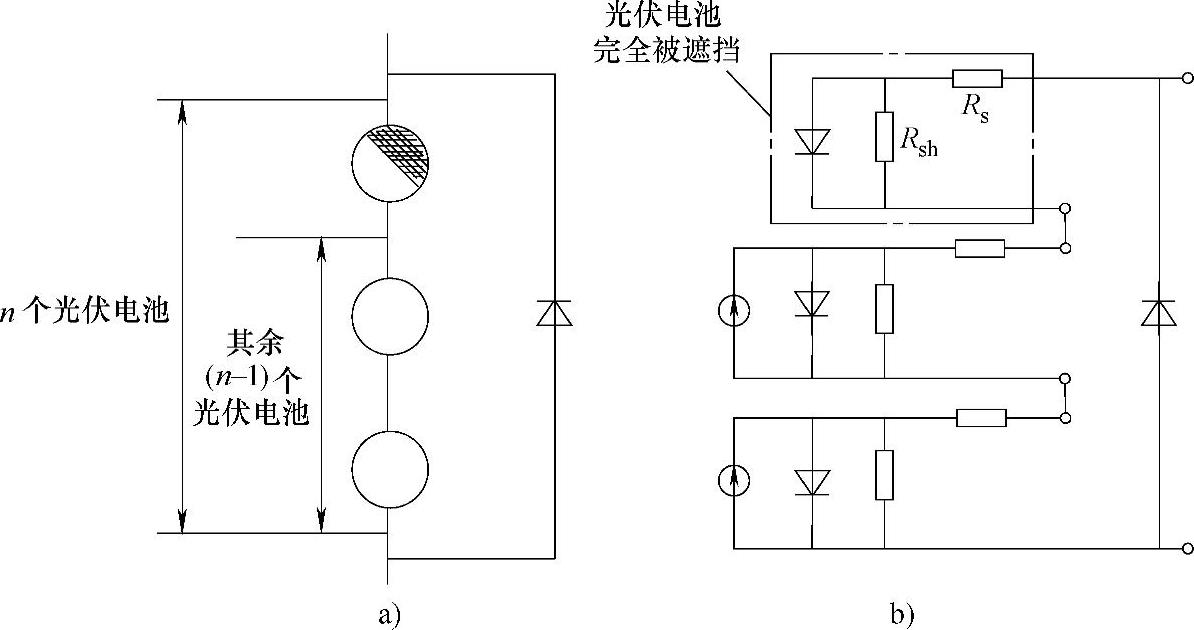
图6-40 n块光伏电池串联及遮挡时的等效电路

a）n块光伏电池的串联结构示意 b）某块光伏电池被完全遮挡时的等效电路

在n块光伏电池串联的组件中，若其中某一块光伏电池被完全遮挡时，则该光伏电池将作为负载消耗支路上其余光伏电池所产生的能量。图6-40b为某块光伏电池被完全遮挡时的等效电路图，针对这一等效电路，完全被遮挡电池所消耗的功率及承受的反压为

P_y=I²_sc（R_sh+R_s）≈I²_scR_sh （6-65）

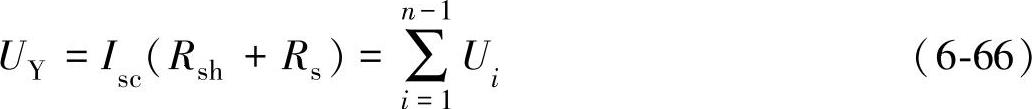
式中 R_sh——并联电阻值；

R_s——串联电阻值；

I_sc——光伏组件短路输出电流；

U_i——无遮挡光伏电池的输出电压。

一般而言，若光伏电池属于电压限制型电池（A类）时，其并联电阻较大，局部遮挡时消耗功率最大，即最严重的热斑效应发生在局部遮挡时；若光伏电池属于电流限制型电池（B类）时，其并联电阻较小，完全遮挡时消耗功率最大，即最严重的热斑效应发生在该光伏电池被完全遮挡的情形下。

显然，A类电池由于并联电阻较大，因此，可以通过减少遮光面积来达到最佳阻抗匹配。

当某块光伏电池被部分遮挡时，在某个特定的遮挡条件下，若与其余光伏电池的内阻形成特定的匹配，则该光伏电池消耗的功率达到最大值，从而产生最严重的热斑效应。图6-41为某块光伏电池被部分遮挡时的等效电路以及输出的U-I特性曲线。图6-41中使用两个并联电池等效光伏电池部分情形。

图6-41 某块光伏电池被部分遮挡时的等效电路及其输出的U-I特性曲线

a）等效电路 b）特性曲线

由图6-41可知，其未遮挡的n-1块光伏电池串的U-I特性曲线对y轴的镜像（如虚线所示）与被遮挡光伏电池的U-I曲线的交点W处的电压和电流值共同确定了被遮挡的光伏电池所消耗的功率（阴影面积），而W点处的电流值正是光伏组件的短路电流I_sc。当该短路电流等于其余n-1块光伏电池的最大功率点电流，即I_sc=I^n-1_mpp时，被遮挡的光伏电池所消耗的功率最多，所以被遮挡光伏电池消耗的功率最大值不大于其余n-1块光伏电池的最大输出功率。总之，被遮挡的光伏电池所消耗的功率与遮挡面积和遮挡强度都有关系，并且当W点电流值与其余n-1块光伏电池的最大功率点输出电流I^n-1_mpp相等时，达到最大。

以上分析表明：被遮挡的光伏电池的输出电流一旦确定，整条支路的输出电流值也就被确定。而未被遮挡的光伏电池发电量越大，消耗在被遮挡光伏电池上的能量也就越多。因此，当在其余n-1块未被遮挡的光伏电池工作在相应的最大功率点时，相应光伏电池的发电量最大，消耗在被遮挡光伏电池上的能量也就最多。

当被遮挡的光伏电池反向电压值达到该光伏电池的反向雪崩击穿电压值时，光伏电池内部的pn结发生雪崩击穿，流过该光伏电池的电流急剧上升，反向电压也大幅增长，从而出现严重的热斑效应，当热斑温度达到一定值时，pn结被热击穿，从而使光伏电池损坏，该支路也因此无法继续正常工作。

为了限制热斑效应强度，通常的做法是为光伏电池串反并联旁路二极管，如图6-42所示。正常工作情形下，旁路二极管处于反偏状态，不影响光伏电池的工作情形；当该块光伏电池被遮挡时，被遮挡的光伏电池成为负载，开始消耗其余光伏电池发出的电能，此时旁路二极管导通，支路电流中超过被遮挡光伏电池光生电流的部分被二极管分流，从而限制了被遮挡光伏电池的端电压，避免了被遮挡光伏电池因产生严重的热斑效应而损坏。

从理论上说，为每块光伏电池并联一个旁路二极管可以消除热斑效应。当旁路二极管导通时，其自身的管压降会使整条支路的电压减小0.6V左右，当被遮挡光伏电池的数量比较多时，旁路二极管的导通压降会带来额外功率损失；因此，一般不会给光伏组件中每块电池配一个旁路二极管，而是一组（若干块电池）配一个旁路二极管，如图6-43所示。

图6-42 光伏电池并联旁路二极管工作示意图

6.7.1.2 光伏阵列的多峰值特性

当光伏阵列中的部分光伏电池由于阴影、灰尘等原因出现局部遮挡而使其光照和温度等外界条件发生变化时，被遮挡光伏电池的输出特性即会发生改变，从而出现较为明显的不匹配情形（局部最大功率点），造成光伏阵列的输出功率损失和热斑效应。为了减小不匹配情形带来的功率损失和热斑效应，实际中常常为若干块电池反并联一个旁路二极管，但是旁路二极管的引入又带来了光伏阵列在不匹配情况下的多峰值特性，给光伏阵列的最大功率点跟踪控制带来困难。

正常工作条件下，光伏电池的P-U特性为一条单峰值曲线，光伏阵列亦是如此。本节以图6-43所示的m个光伏电池串联的情形为例，介绍局部最大功率点的形成过程。

从而导致被遮挡的光伏电池的U-I特性曲线上短路电流值的下降；同时，由于遮挡导致光伏电池温度升高，其相应的开路电压值也会相应减小。显然，当光伏阵列中的某块电池被遮挡时，其光伏阵列的输出特性也会发生变化，即：这时整个光伏阵列的U-I特性曲线上会出现两个膝点，如图6-44b所示，而对应的P-U特性曲线上则可能会出现两个峰值点，如图6-44c所示。

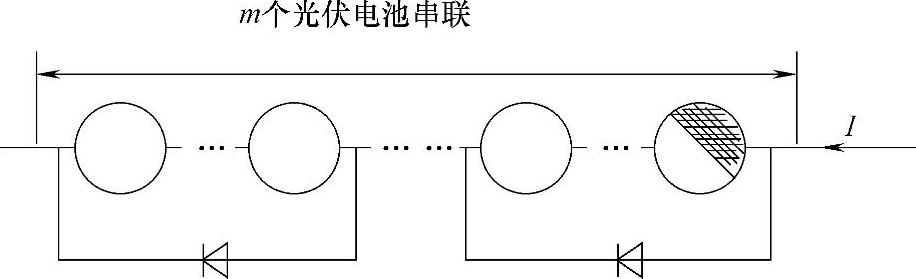
图6-43 m块光伏电池串联示意图

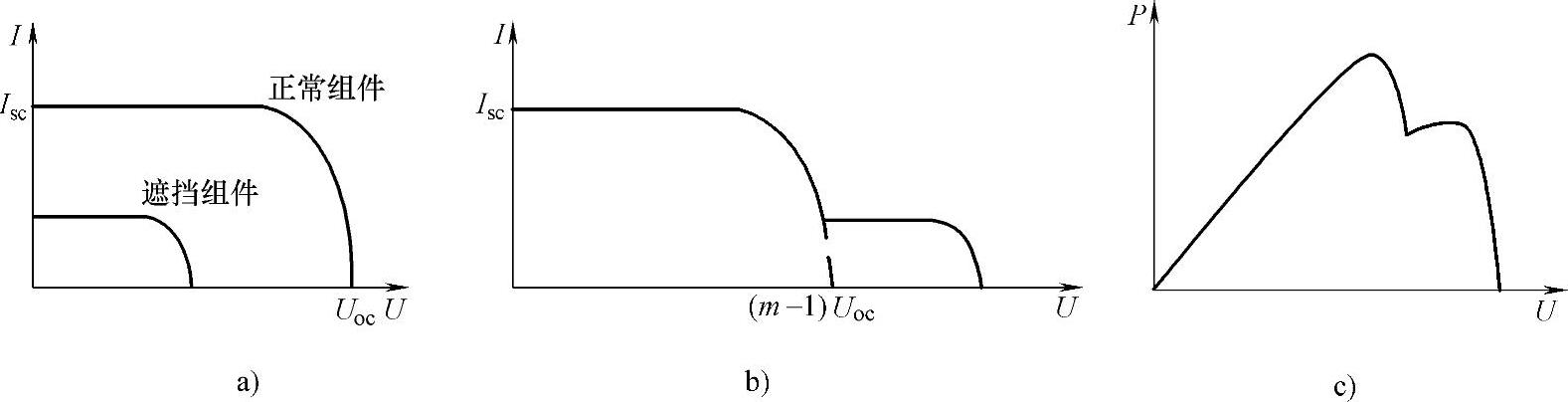
图6-44 某一块光伏电池被遮挡时的光伏电池/阵列的输出特性

a）光伏电池的输出U-I特性 b）光伏阵列的输出U-I特性 c）光伏阵列的输出P-U特性

当多块光伏电池被遮挡且遮挡的程度不同时，情况更为复杂。对于如图6-43所示的串联光伏阵列中，若有两块光伏电池被遮且遮挡的程度不同时，整个光伏阵列的U-I特性曲线上会出现三个膝点，对应的P-U特性曲线上则可能会出现三个峰值点，如图6-45所示。

可见，当光伏阵列中出现多块光伏电池被不同程度遮挡时，整个光伏阵列的U-I特性曲线上必然会出现多个膝点，而对应的P-U特性曲线上则会出现多个峰值点。分析表明，当光伏电池被遮挡时，对应光伏阵列P-U特性曲线上的峰值点数小于等于光伏阵列U-I特性曲线上的膝点数，即当光伏阵列的U-I特性曲线上出现膝点时，相应的P-U特性曲线上并不一定出现峰值点。

下面仍以光伏阵列中有两块光伏电池被遮挡时的情况加以讨论。为分析方便，把遮挡状态按强度排列：依次为正常光照，遮挡1，遮挡2；对应的短路电流值和最大功率点电流值分别为I_sc、I_sc1、I_sc2和I_mpp、I_mpp1、I_mpp2。这样便存在以下几种光伏阵列P-U特性曲线上的峰值点数小于光伏阵列U-I特性曲线上的膝点数情况，分析如下：

（1）当遮挡1光伏电池的U-I特性与正常光照光伏电池的U-I特性相近时

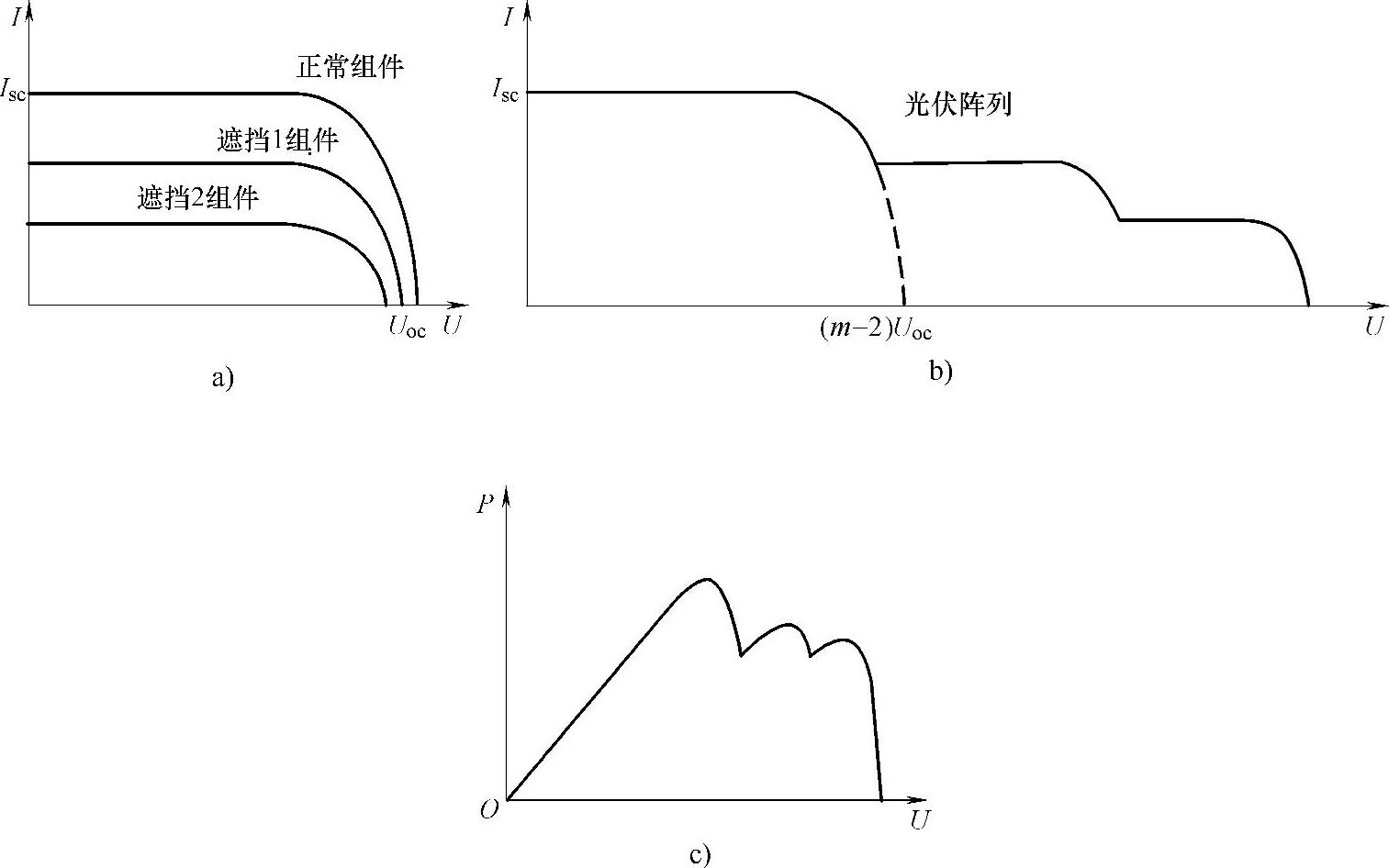
图6-45 某两块光伏电池被遮挡时的光伏电池/阵列的输出特性

a）光伏阵列的U-I特性分解图 b）光伏阵列的U-I特性 c）光伏阵列的P-U特性

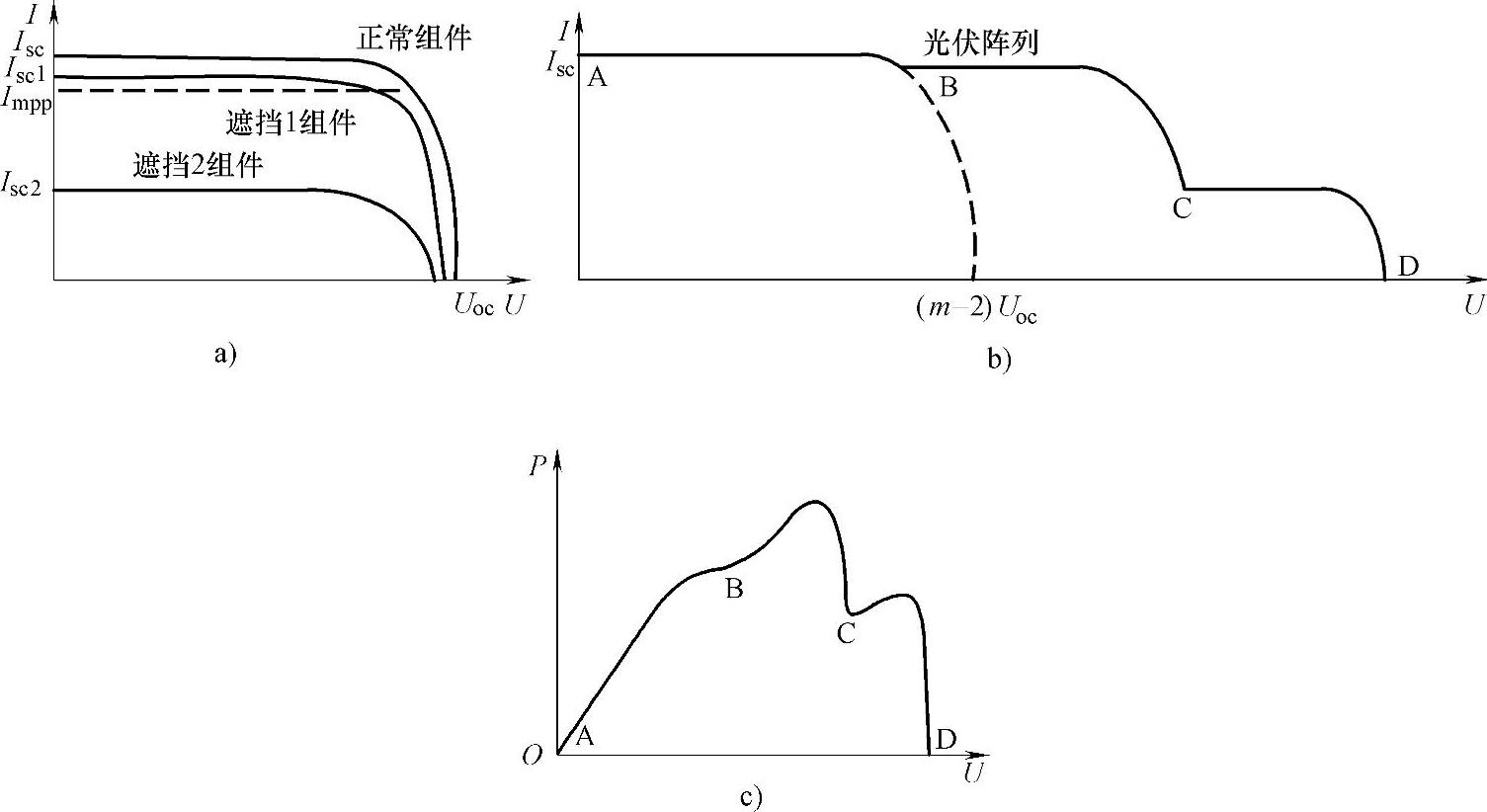
图6-46 当遮挡1的U-I特性与正常光照的U-I特性相近时的光伏电池/阵列的输出特性

a）光伏阵列的U-I特性分解图 b）光伏阵列的U-I特性 c）光伏阵列的P-U特性

从图6-46中可以看出：当遮挡1光伏电池的U-I特性与正常光照光伏电池的U-I特性相近时，I_mpp＜I_sc1＜I_sc，此时，光伏阵列U-I特性曲线上出现3个膝点，如图6-46b所示，分别位于AB、BC和CD3段上，但如图6-46c所示的光伏阵列P-U特性曲线上只出现了两个峰值点，而不会出现3个峰值，这是因为：AB段为单峰值曲线的上升段，当其还未到峰值点时，即切入到另一条单峰值曲线BC段的上升段，因此光伏阵列P-U特性曲线的AB段不会出现峰值点，即整个光伏阵列P-U特性曲线上只出现了两个峰值点。

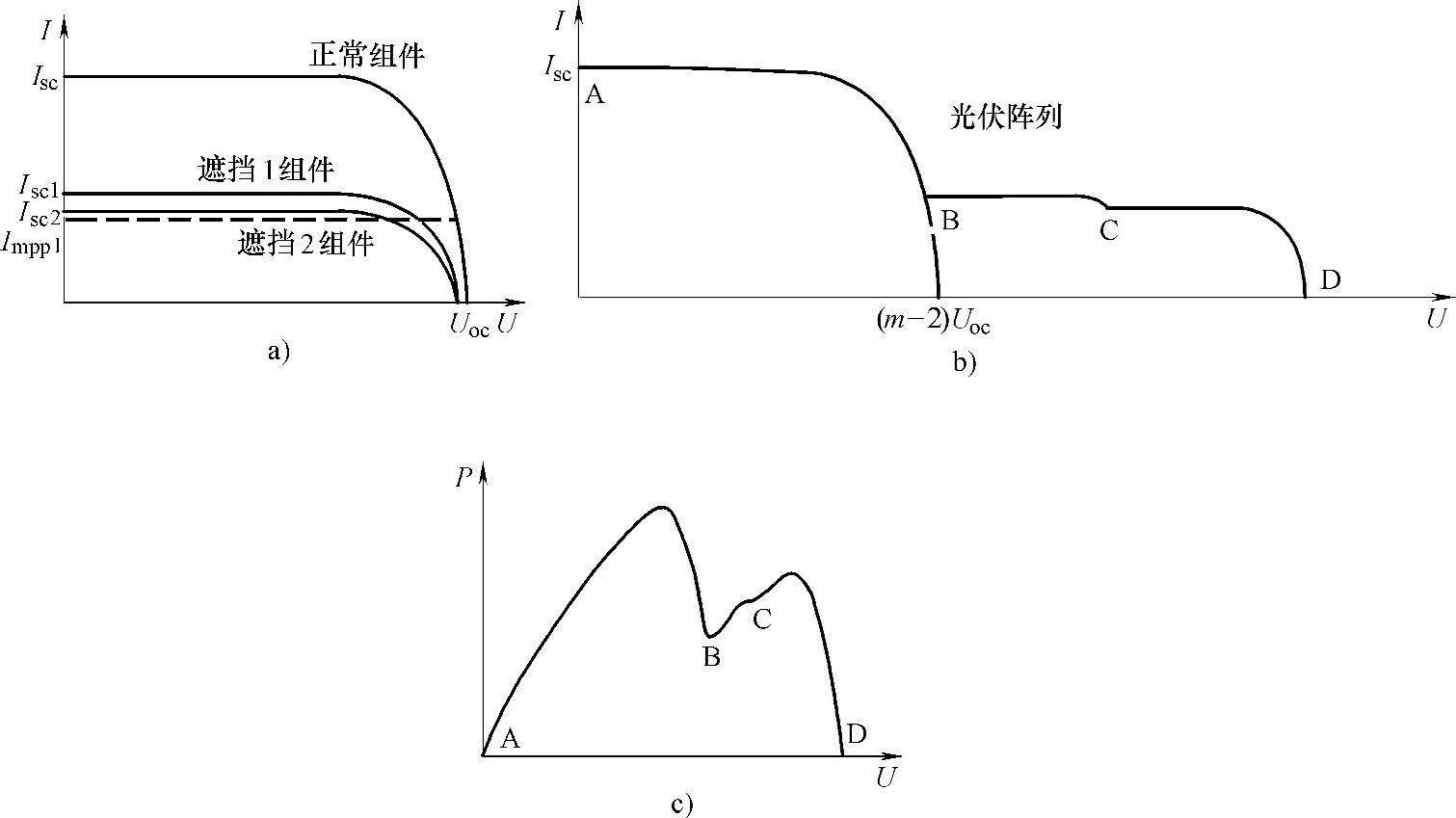
图6-47 遮挡1的U-I特性与遮挡2的U-I特性相近时的光伏电池/阵列的输出特性

a）光伏阵列的U-I特性分解图 b）光伏阵列的U-I特性 c）光伏阵列的P-U特性

（2）当遮挡1光伏电池的U-I特性与遮挡2光伏电池的U-I特性相近时

当遮挡1光伏电池的U-I特性与遮挡2光伏电池的U-I特性相近时，I_mpp1＜I_sc2＜I_sc1。同理，对应到图6-47所示的光伏阵列的输出P-U特性曲线上BC段的峰值消失，也不会出现3个峰值点。

（3）当遮挡1光伏电池、遮挡2光伏电池的U-I特性与正常光照光伏电池的U-I特性相近时

当遮挡1光伏电池、遮挡2光伏电池的U-I特性与正常光照光伏电池的U-I特性相近时同理分析，此时不会出现多峰值点，如图6-48所示。

当多串光伏电池并联时，分析类似。

上述分析表明：当多个光伏电池串联组成的光伏阵列被部分遮挡时，光伏阵列的P-U曲线将出现局部最大功率点。此时若采用基于单峰值形态的光伏阵列P-U曲线的MPPT算法即可能会发生误判。另外，因此有必要研究多峰值条件下光伏阵列的最大功率跟踪方法，为了更加理解光伏电池在阴影条件下的输出特性，需要更加全面、准确地描述光伏电池在遮挡时的特性，下面简单介绍一下光伏电池的双二极管模型，如图6-49所示。

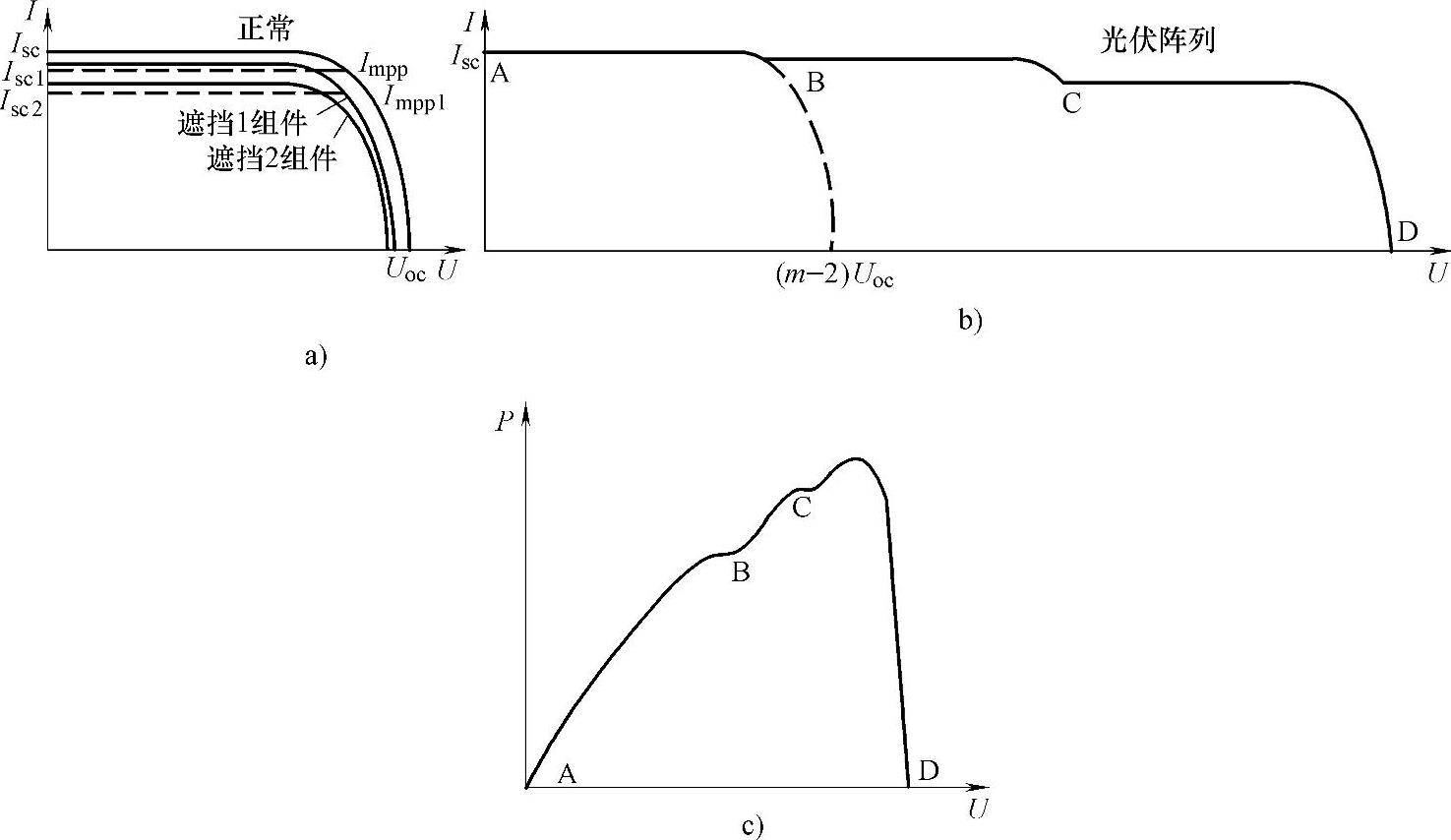
图6-48 当遮挡1和遮挡2的U-I特性与正常光照的U-I特性相近时的光伏电池/阵列的输出特性

a）光伏阵列的U-I特性分解图 b）光伏阵列的U-I特性 c）光伏阵列的P-U特性

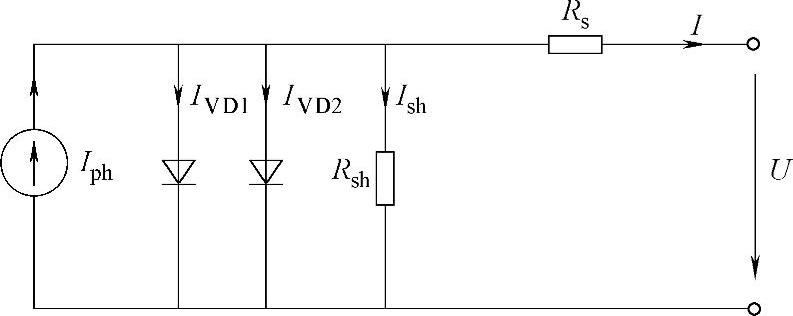
图6-49 双二极管模型

在双二极管模型中，其输出特性方程为

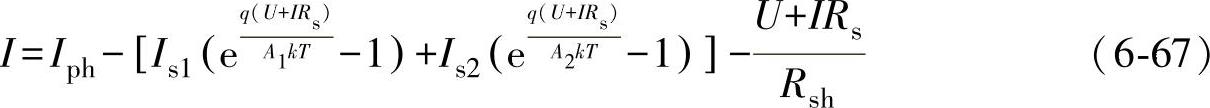
式中 I——光伏电池电流；

I_ph——光生电流；

I_s1——与p区和n区中电子和空穴的分离和复合相关的二极管饱和电流；

I_s2——与耗尽层中电子和空穴的分离和复合相关的二极管饱和电流；

U——光伏电池电压；

R_sh——并联电阻；

R_s——串联电阻；

A₁——第一个二极管的品质因数；

A₂——第二个二极管的品质因数；

T——光伏电池绝对温度；

q——单位电荷（1.6×10^-19C）；

k——波尔兹曼常数（1.38×10^-13J/K）。

显然，与式（2-8）描述的单二极管模型方程相比，双二极管模型方程多了一个与二极管特性类似的指数项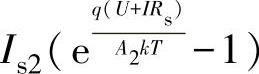，从而可以更准确地描述光伏电池的暗特性。光伏电池的暗特性是指当光伏电池完全被遮挡（即光伏电池中的光生电流I_ph为0）时的输出特性，暗特性是影响光伏电池输出特性的一个重要因素，实际中常利用暗特性来评估光伏电池的品质。由于光伏电池暗特性反映的电流流向与光生电流I_ph相反，因此暗特性中电流的数值越大，光伏电池正常工作时的漏电流数值也越大，同等条件下的发电量也越低。

从式（6-67）可以看出：当光伏电池被遮挡时，光生电流I_ph数值减小，此时模型方程中的串联电阻R_s的阻值也相应变大，光伏电池的漏电流数值也相应增加，这使得光伏电池中漏电流与光生电流比值发生变化，从而影响了光伏电池输出特性曲线的变化。

从物理意义的角度来说，光伏电池具有p-n结特性，因而在材料表面以及内部少子的恢复电流对其输出特性有一定的影响。式（2-8）给出的单二极管模型忽略了其中p-n结耗尽层少子的恢复运动，而仅仅考虑p区与n区中由于少子的运动产生的恢复电流。实际上，双二极管模型是在单二极管模型的基础上衍生而来的，与单二极管模型不同的是：双二极管模型将其中的漏电流I_d分成了I_d1和I_d2两部分，并分别由两个二极管等效。其双二极管模型中的第一个二极管用来等效由较大的前向偏置电压决定的p区与n区之间由于少子运动产生的恢复电流，这与单二极管模型中的二极管等效作用相同；而双二极管模型中添加的第二个二极管则用来等效耗尽层中由于能量的激发可能产生的少子的恢复运动，从而使光伏电池模型可以更精确地描述光伏电池的漏电流特性[28-30]。显然，当光伏阵列被局部遮挡时，相关被遮挡光伏电池的漏电流特性直接影响到光伏阵列的输出特性，此时，光伏电池双二极管模型的优越性便体现了出来。(www.xing528.com)

6.7.1.3 多峰值条件下的MPPT方法

如前所述，当多个光伏组件串联组成的光伏阵列被部分遮挡时，光伏阵列的P-U曲线将会呈现出多峰值特性，此时若还采用单峰值形态的MPPT算法去跟踪光伏阵列P-U曲线的最大功率点，就可能会发生误判，因此必须研究适用于存在局部最大功率点的多峰值MPPT方法。以下介绍两种基本的方法。

1.两步法^[31]

在多峰值MPPT方法中，全局扫描法通过扫描光伏阵列的全部输出特性曲线，可以确保跟踪到多峰值曲线的最大功率点，但过长的非最大功率点区域的搜索会造成过多的能量损耗。为了克服全局扫描法存在的不足，Kenji Kobayashi等人针对双峰值光伏阵列P-U曲线提出了两步法。

在光伏阵列输出特性呈现出的各种多峰值情形中，双峰值P-U曲线具有十分典型的意义，其出现的概率最大，图6-50给出了双峰值的两种情形。对图6-50a所示的第一种P-U特性曲线，由于常规MPPT算法启动时的工作点是从开路电压向最大功率点移动的，因此针对图6-50a所示的第一种P-U特性曲线，由于真正的最大功率点电压靠近开路电压处，此时常规的MPPT算法不会发生最大功率点误判；然而图6-50b所示的第二种P-U特性曲线，由于真正的最大功率点电压远低于开路电压，常规的MPPT算法则可能工作于一个虚的最大功率点（局部的最大功率点），而非真正的最大功率点，从而发生最大功率点误判。

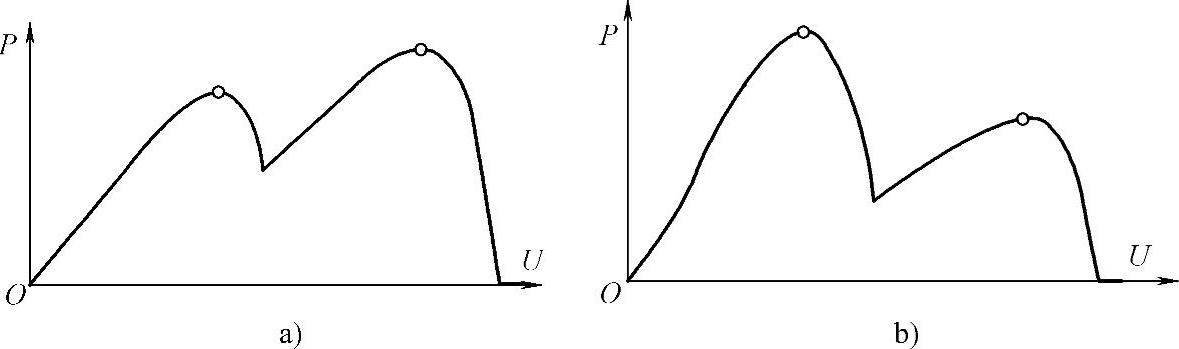
图6-50 辐照度不均匀情况下的光伏阵列特性

为了能够快速、准确地跟踪到双峰值条件下光伏阵列的全局最大功率点，下面将首先分析双峰值情况下，全局最大功率点的分布特性，进而讨论解决局部最大功率点问题的两步法及其跟踪过程。

在辐照度不均匀的情况下，光伏阵列的U-I、P-U曲线呈现不同的形状，并可以由下面公式近似表达：

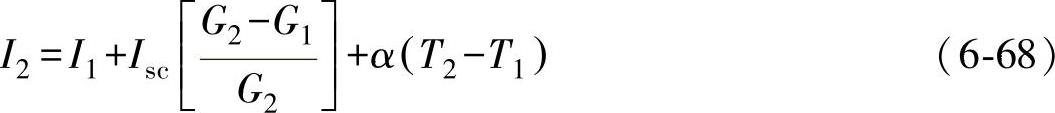
U₂=U₁+β（T₂-T₁）-R_s（I₂-I₁）-KI₁（T₂-T₁） （6-69）

式中 α——光伏阵列表面温度每改变1℃时I_sc的改变量；

β——光伏阵列表面温度每改变1℃时U_oc的改变量；

R_s——等效串联电阻；

K——电流修正系数；

U₁、I₁——在辐照度G₁和温度T₁时的输出电压和电流值；

U₂、I₂——在辐照度G₂和温度T₂时的输出电压和电流值。

在图6-51所示的光伏阵列双峰值I-U特性曲线中，首先定义等效负载电阻线及阴影参考线为

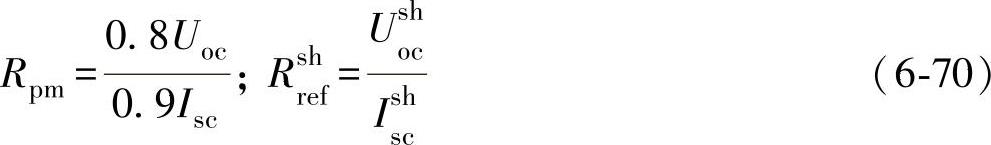
式中 I_sc、U_oc——在线测得的光伏阵列短路电流和开路电压；

I^sh_sc——被遮挡的光伏组件的短路电流；

U^sh_oc——没有遮挡的光伏组件的开路电压；

R_r^sh_ef——阴影参考线；

R_pm——等效负载电阻线。

对于图6-51所示的不同情形，光伏阵列双峰值特性显然都存在两个峰值功率点B点和D点。其中：左侧峰值点B点的功率可近似表示为P^B_mpp≈U^sh_oc×0.9I_sc，而右侧峰值点D点的功率可近似表示为P^D_mpp≈I^sh_sc×0.8U_oc。在图6-51a中，由于D点是全局最大功率点，因此P_m^D_pp＞P^B_mpp，此时有R_pm＞R^sh_ref，等效负载电阻线与光伏阵列的I-U特性曲线的交点为C点，显然其交点C位于恒流区；同理，图6-51b中B点是全局最大功率点，即P^D_mpp＜P^B_mpp，此时等效负载线与光伏阵列的I-U特性曲线的交点C点位于恒压区。显然，通过对图6-51所示两种不同位置最大功率点的情况分析可见：等效负载电阻线与光伏阵列的I-U特性曲线的交点位置反映了全局最大功率点所在的区域，这样在跟踪最大功率点时，只要找到了等效负载电阻线与光伏阵列的I-U特性曲线的交点，也就确定了全局最大功率点所在的区域，确定了全局最大功率点所在区域后，再使用传统的MPPT方法即可完成最大功率点跟踪。综上所述，双峰值特性曲线上的全局最大功率点的跟踪过程可以概括为以下两步：

第一步，快速搜索光伏阵列I-U特性曲线与等效负载电阻线的交点，如图6-51a、b所示中的C点。

第二步，从第一步搜索到的交点处，开始使用单峰值MPPT方法完成最大功率点跟踪，如图6-51a中的D点和图6-51b中的B点。

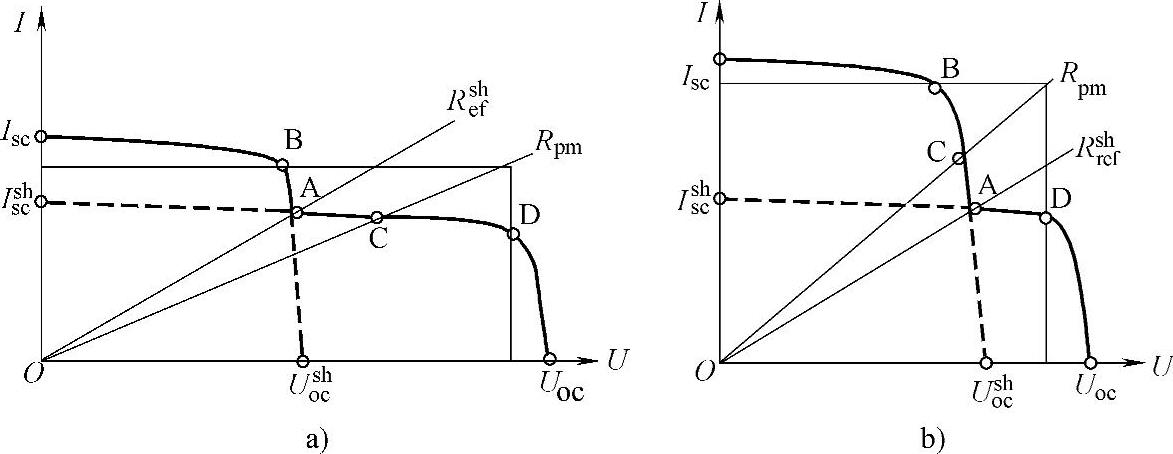
图6-51 两步法示意图

a）最大功率点在右侧时的情况 b）最大功率点在左侧时的情况

然而上述的两步法在实施中可能遇到以下两种情况：

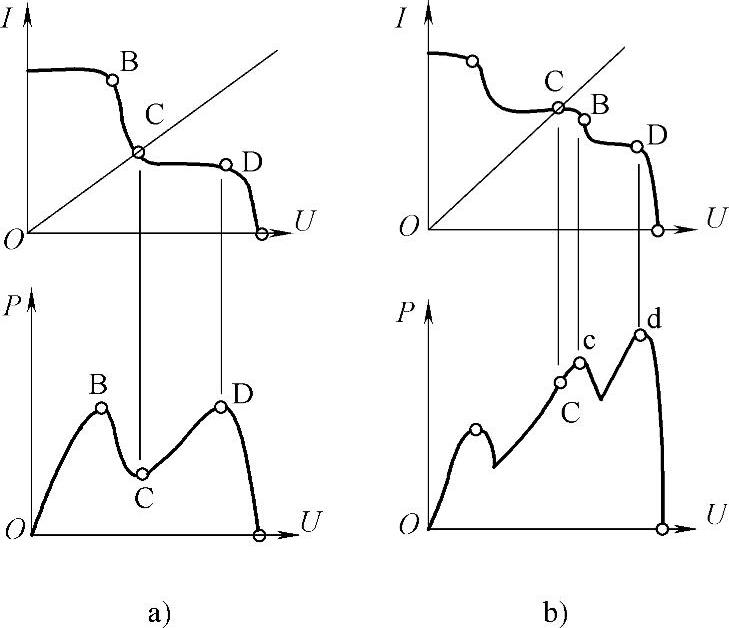
图6-52 两步法工作过程示意图

a）交点在极小值点 b）多峰值情形

1）如图6-52a所示，当第一步操作结束后，交点C本身为一个极小值点，此时dP/dU等于零，系统会直接停留在C点，从而无法搜索到最大功率点；

2）如图6-52b所示，当第二步在使用传统MPPT方法搜索的区域内出现多个极值点时，两步法仍然无法找出真正的最大功率点。即光伏阵列输出曲线超过两个极值点时，可能会导致两步法的误判。

两步法是一种较为简单的多峰值最大功率点跟踪方法，其主要不足在于：1）不能确保跟踪到全局最大功率点，即存在误判情形；2）等效负载电阻线的计算需要附加在线测量短路电流和开路电压的电路；3）跟踪过程中，光伏阵列存在开路状态和短路状态，增加了光伏系统的功率损耗。

2.改进的全局扫描法（POC）^[32]

由于两步法在如图6-52a、b所示的情形下不能正确判定出最大功率点，因此这种方法存在一定的局限性。对于多峰值情况下的最大功率点跟踪，最可靠的方案就是全局扫描法，全局扫描法通过扫描全部的输出特性曲线，虽然可以确保跟踪到多峰值曲线的最大功率点，但过长的非最大功率点区域搜索会造成相应的能量损耗。为了减少搜索过程造成的能量损耗，同时克服两步法的不足，下面介绍一种可以有效减少系统在非最大功率点区域搜索时间的全局扫描方法——改进的全局扫描法，由于该方法在搜索局部极值时，使用了扰动观测法，因此其实际上又是一种改进的扰动观测法，又称POC算法（Perturb，Observe and Check Algorithm）。

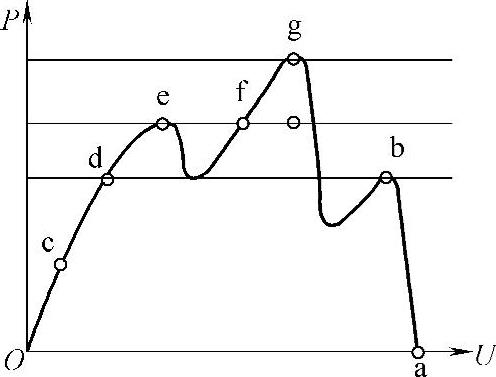
图6-53 光伏阵列多峰值P-U特性曲线

图6-53给出了某种遮挡情况下的具有多峰值特性的光伏阵列P-U特性曲线，在这种多峰值情形下，由于POC算法采用的是全局扫描的思想，因此可以确保搜索出最大功率点。另外，由于POC算法采用了一种快速扫描机制，因此可以用相对较少的时间完成光伏阵列P-U曲线的全局扫描。POC算法的主要步骤可以分为两个部分。具体讨论如下：

1）首先系统采用常规的扰动观测法从开路电压处（图6-53中a点）开始向电压值减小的方向搜索出第一个峰值点（图6-53中b点），系统检测出第一个峰值点后，记录下第一个峰值点的信息，并将该数据存储为最大功率点数据（此步骤中使用的扰动观测法也可以被其他自寻优类算法如电导增量法替换）。

2）从系统可以工作的最小电压值处（接近短路电流处，见图6-53中c点）开始扫描光伏阵列I-U曲线，通过功率值的比较判别，快速通过功率值小于已知最大功率点功率的区域（见图6-53中点c～d、e～f区域）。对于功率值大于已知最大功率点功率的区域（见图6-53中点d～e、f～g区域），则用扰动观测法搜索出该区域内的局部最大功率点（见图6-53中e点），然后用新的最大功率点（图6-53中e点）的功率值替换前一步搜索得到的最大功率值（图6-53中b点）。重复上述过程，直到确定整个I-U曲线上不存在功率值大于已知最大功率点功率的区域为止。最后将工作点设定为记录中的最大功率点（图6-53中f点）即可。

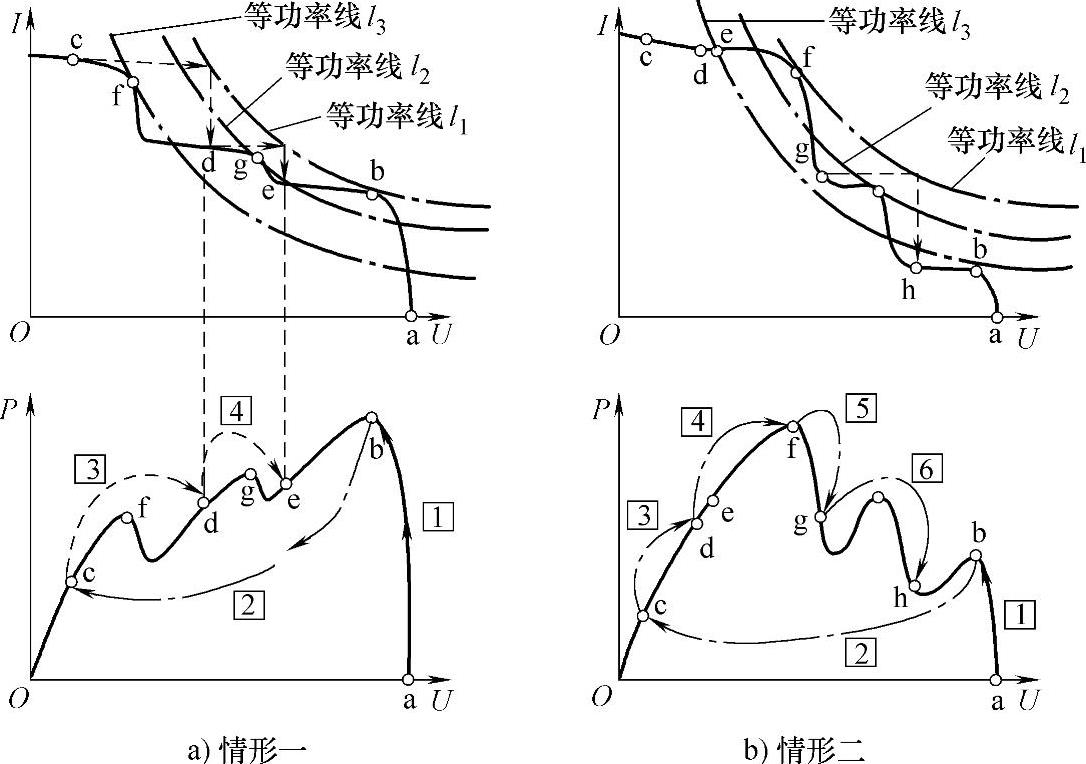
图6-54 使用POC算法搜索过程示意图

a）情形一 b）情形二

下面以图6-54a、b所示两种不同的光伏阵列多峰值输出特性曲线为例，具体描述POC算法的具体搜索过程：

第一步：初始峰值点的搜索，如图6-54a、b P-U曲线中的步骤1。

采用常规的扰动观测法搜索出离光伏电池开路电压点（图6-54中“a”点）最近处的第一个峰值点（图6-54中“b”点），第一个峰值点的搜索过程在此不再赘述。第一步搜索过程完成后，系统中记录的最大功率点的信息为P_mpp=P_b，V_mpp=V_b，I_mpp=I_b。

第二步：转移到最左侧工作点，如图6-54a、b P-U曲线中的步骤2。

由于光伏阵列I-U曲线上各极值点电压之间存在着的最小电压差，这个电压差可以用开路电压附近的极值点电压U_b与旁路二极管个数N相除得到，即

由于光伏阵列I-U曲线上最左侧的极值点的电压不可能小于最小电压差。因此在第一步搜索过程完成后，系统将直接跳转到电压等于最小电压差的工作点（图6-54中“c”点）工作。

第三步：快速扫描光伏阵列I-U曲线，如图6-54a P-U曲线中的步骤3、步骤4。

由于图6-54中“b”点在等功率曲线l₁上，而等功率线l₁左下部分工作点的输出功率均小于P_b，因此这部分曲线上不可能出现全局最大功率点，应该快速越过这个区域。此时采用式（6-71b）来计算下一步的工作点电压。而且当式（6-71c）满足时，结束搜索过程。

U_n+1-U_b＜U_min （6-71c）

式中 P_mpp——此刻记录在系统中的最大功率值；

I_n——系统上一个采样点的电流值；

U_n+1——系统通过以上信息确定的下一步工作点电压值；

N——光伏阵列反并联的旁路二极管数；

U_min——光伏I-U曲线上不同最大功率点之间的最小间隔。

以上描述的三个步骤就是POC方法搜索的基本过程，但在POC法搜索过程中还有两点需要讨论：

1）在图6-54b中I-U曲线上的d点，如何判断d点的右侧存在输出功率比最右侧最大功率点（图6-54b中“b”点）大的工作点？

2）在图6-54b中I-U曲线上，如果已经搜索到图6-54b中“f”点，下一步的工作点电压如何确定，即如何转移到图6-54b中“g”点？

对于上述问题1）：当系统工作在图6-54b中的d点时，如果继续按照式（6-71b）计算下一步的工作点电压，跟踪过程将会陷入图6-54b中的e点，即系统工作点会无限接近e点，但不能越过e点。针对这个问题，POC法中引入了式（6-72a）的判据，如果式（6-72a）满足，则认为当前工作点的右侧存在输出功率比最右侧最大功率点，系统转为常规的扰动观测法工作，并且实时更新记录中的最大功率点信息，跟踪过程完成后记录中的最大功率点（图6-54b中“f”点）信息为P_mpp=P_f，U_mpp=U_f，I_mpp=I_f。

对于上述问题2）：当系统使用常规的扰动观测法，搜索到图6-54b中的f点，常规的扰动观测法将会稳定在此点工作。为了解决这个问题，POC算法在用常规的扰动观测法搜索到局部最大功率点后，利用光伏阵列I-U曲线上极值点之间的最小电压差来确定下一步的工作点电压，即按照式（6-72b）来实现工作点的转移。

U_n+1-U_n＜ΔU （6-72a）

U_n+1=U_mpp+U_min （6-72b）

式中 ΔU——为常规的扰动观测法MPPT的最小步长。

POC算法完整的流程图如图6-55所示。

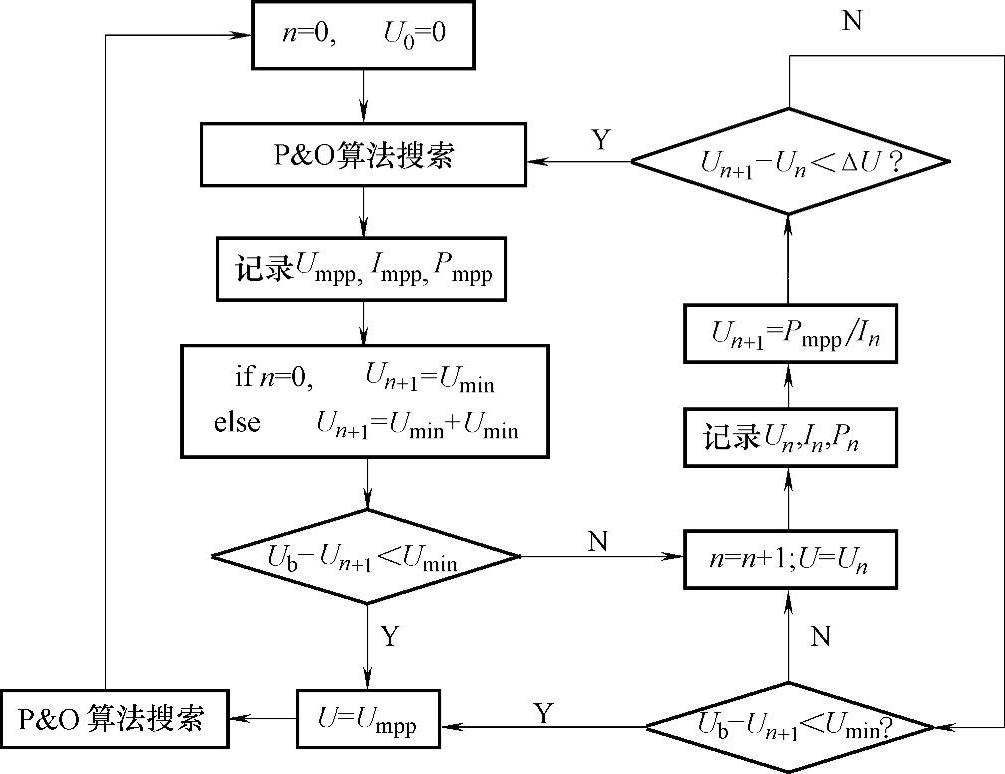
图6-55 POC算法流程

注：图中P&O算法的流程请参见图6-7。

通过以上分析可知，POC算法克服了两步法在某些情形下不能判断出最大功率点的缺陷，并且由于快速转移机制的引入，使得系统较快地越过了不可能出现最大功率点的区域，从而可以使系统在局部最大功率点发生的情形下，仍然可以快速、准确地跟踪到最大功率点。但是由于POC算法在跟踪过程中需要从短路电流处的工作点（图6-54a、b中“c”点）开始搜索，所以要求控制电路具有较宽的工作电压范围，同时该方法仍然使用全局扫描的思路，因此在搜索的快速性上尚有不足，特别是最右侧的极值点的功率值比较小时，会导致较多的能量损耗。