电导增量法的改进方案

基于上文对振荡和误判问题的讨论，本节提出了电导增量法的几种改进方法，其中基于变步长的电导增量法对于振荡具有较好的抑制效果，基于功率预测的电导增量法有效地解决了外部环境剧烈变化时产生的误判问题，而基于中心差分法的电导增量法则有效抑制了振荡和误判的发生，提高了MPP的跟踪精度。

6.4.3.1 基于变步长的电导增量法^[12-14]

常规的电导增量法大多采用定步长方式进行最大功率点跟踪。然而，这种定步长的电导增量法存在明显缺陷：若步长过小，会使光伏电池较长时间滞留在低功率输出区域；若步长过大，又会加剧系统振荡。针对6.4.2.1节中指出的振荡问题，为了提高电导增量法进行最大功率跟踪时的快速性和准确性，与扰动观测法类似，可以采用变步长的电导增量法。具体的变步长方法可以参考扰动观测法中的变步长方法，下面只简述两种变步长的电导增量法的基本思路。

1）基于光伏电池P-U特性曲线的变步长电导增量法的基本思路。由光伏电池的P-U特性曲线特征可以看出：在整个电压范围内功率曲线为一单峰函数，在最大功率点电压U_mpp处dP/dU=0，而在U_mpp两端则dP/dU均不为0。如果采用变步长的电导增量法，则要求：在远离最大功率点区域，跟踪的步长适度变大，以提高MPPT跟踪速度；而在最大功率点附近区域，系统跟踪的步长适当变小，以提高MPPT跟踪精度。显然，可以考虑将步长设计为dP/dU的函数，即令步长ΔU=A×dP/dU，通过设置合适的A，就可以实现基于变步长电导增量法的MPPT控制。

2）基于光伏电池U-I特性曲线的变步长电导增量法的基本思路。观察图6-1中的U-I特性曲线可知，类似恒流源区域与类似恒压源区域范围的比例大约为4∶1。采用变步长电导增量法时总是希望系统在类似恒流源的区域里加大步长以提高跟踪速度，而在类似恒压源的区域里减小步长以提高跟踪精度。具体步骤是：首先，通过检测电压变化时的电流变化率，判断出光伏电池所在的工作区域：在类似恒流源的区域，电流变化率很小，而在类似恒压源的区域，电流变化率很大；然后，根据工作区域的不同可以设定不同的步长，在类似恒流源区域步长适当加大，在类似恒压源的区域步长适当减小；最后，利用电导增量法判据判断系统是否已经工作在最大功率点，如果满足判据要求，则停止扰动。

6.4.3.2 基于功率预测的电导增量法

在辐照度不变的条件下，使用电导增量法可以跟踪到最大功率点。由6.4.2.2节可知，辐照度时刻变化，随时可能发生的误判直接导致了功率的损耗。对于6.4.2.2节指出的误判问题，与扰动观察法类似，可以采用基于功率预测的电导增量法予以克服。功率预测方式的引入使预测的功率点与下一扰动测量得到的功率点近似位于同一条U-I曲线上，从而避免了误判现象的发生。从而在辐照度变化的情形下，仍然可以采用电导增量法搜索最大功率点。

在6.4.2.2节中，图6-21给出了辐照度发生变化时，常见的误判现象示意。并指出，误判发生的根本原因是辐照度变化前后采样得到的A点和C点的数据隶属于两条不同的光伏曲线。这样对A点和C点采样得到的信息计算后得出的结论便无法正确反映出工作点所在位置，最终导致了误判的发生。

而采用功率预测法则可以有效避免这种误判情形，具体分析如下：

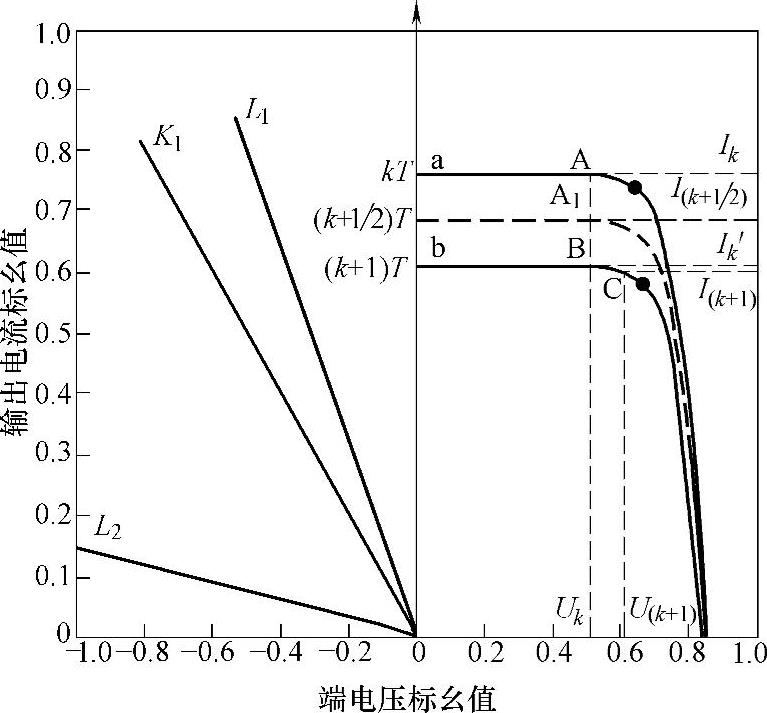
图6-24 基于功率预测的电导增量法原理图

（注：直线L₁、L₂、K₁的定义同6.4.2.2节）

如图6-24所示，若kT时刻系统运行于A点，测得电压、电流值分别为U_k、I_k，此时辐照度发生突变（假设在一个采样周期中辐照度的变化速率恒定），系统并不立即改变工作点电压值，而是在（k+1/2）T时刻增加一次测量（对应A₁点），若测得（k+1/2）T时刻的电流值为I_k+1/2，则可以预测出B点的电流值I_k′为

I_k′=2I_k+1/2-I_k （6-26）

这样，B点和C点可以近似被看做隶属于一条U-I曲线，基于B点和C点的电压、电流值，系统可以对工作点位置以及下一步的搜索方向做出准确的判断。如图6-24所示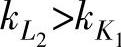，，即

此时，系统判定工作点运行于最大功率点左边，继续增大工作点电压，向右搜索最大功率点，这与实际情况相符，从而有效克服误判现象。

由以上分析可知，基于功率预测的电导增量法在辐照度突变的情况下，能有效克服误判现象，减少了光伏发电的功率损失。

6.4.3.3 基于中心差分的电导增量法^[15]

光伏发电系统中，MPPT通常采用的是建立在极值理论基础之上的线性自寻优技术，在MPPT控制的数字实现时，通常采用差分来近似代替微分。

对于y=f（x），若用差分近似代替微分，则有

其中，Δx=x_k-x_k-1，O（Δx）是截断误差。

显然，这种差分近似代替微分，该方法具有一次精度。

设系统第k次采样的电压和电流值分别为U_k、I_k。根据之前的分析可知，电导增量法的差分运算为

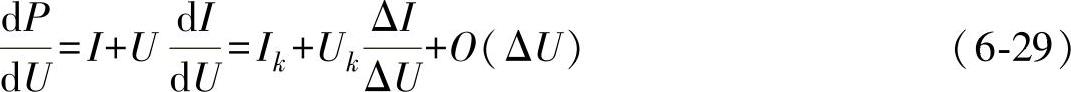
其中，ΔU=U_k-U_k-1，ΔI=I_k-I_k-1。

当求得f′（U，P）≈0的根时，即为所寻找的最大功率点。

由式（6-28）、式（6-29）可知，截断误差的存在正是导致电导增量法不能精确跟踪最大功率点的原因。

在稳态情况下，电导增量法理论上可以使dP/dU=0。在数字化的控制器中，由于截断误差的存在，电导增量法难以精确满足U/I=-dU/dI，即dP/dU=0，从而使输出功率偏离最大功率点功率，导致功率利用率降低。虽然根据式（6-28）、式（6-29）也可以考虑选择较小的步长ΔU来提高差分的精确度，然而由于受数字控制器和检测精度的限制，减小ΔU也是有一定的范围的。因此有必要通过进一步减少截断误差来提高差分运算精度。实际上采用中心差分算法可以进一步减少截断误差，中心差分算法主要考虑以x=x_k为中心的前、后采样点间的差分运算，讨论如下：

首先考虑f（x_k+Δx）在x=x_k处的Taylor展开，即

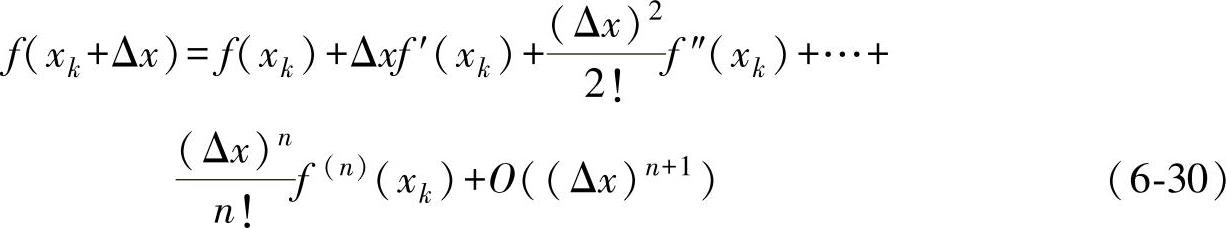
由式（6-30）可以推出：(www.xing528.com)

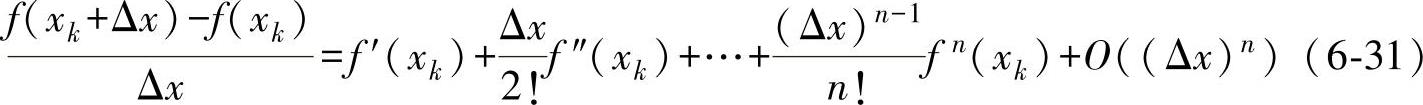
式（6-31）表示了x_k+Δx、x_k间的差分运算，并证明了式（6-28）给出的差分运算具有一次精度。

同理可得x_k、x_k-Δx间的差分运算如下：

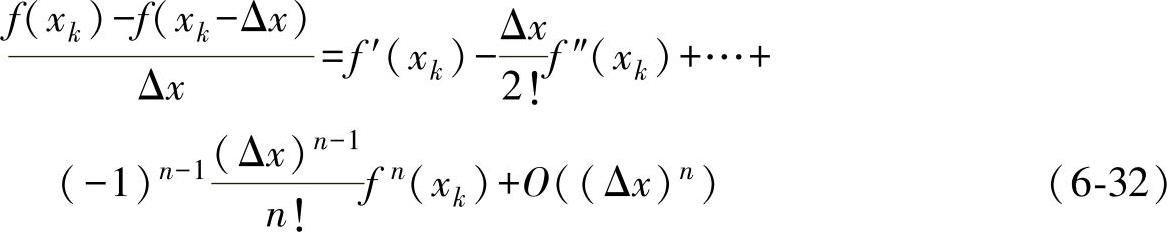
联立式（6-31）和式（6-32）可得以x_k为中心的差分运算，即

式（6-33）可写成：

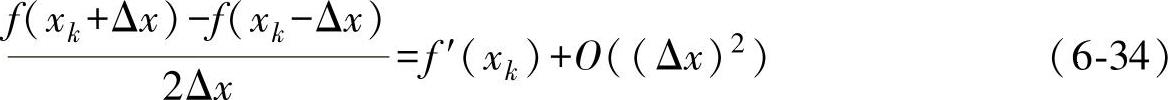
写成中心差分运算表达式，即

其中，Δx=x_k-x_k-1=x_k+1-x_k，O（（Δx）²）是截断误差。

显然，中心差分运算具有二次精度。

对于电导增量法，若采用中心差分运算，则

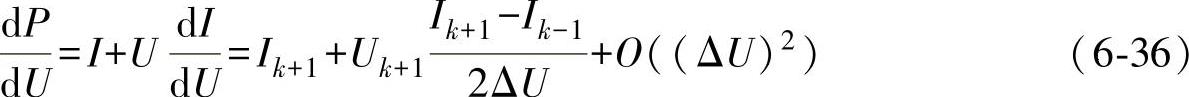
其中，ΔU=U_k-U_k-1=U_k+1-U_k。

从式（6-35）可以看出，误差大小除了与函数本身性质相关外，还取决于Δx的大小。在电导增量法的应用中，函数的本身性质已经确定，误差大小主要取决于ΔU的大小。保证其具有二次精度的前提是数学上需要满足一定约束，即

∣P_k+1-P_k-1∣≤ε∣ΔU∣ （6-37）

其中，系数ε与ΔU无关，需根据实际情形给定。

然而，精度的提高并不能解决工作点位于最大功率点附近的振荡问题。如果能在寻找到最大功率点后停止扰动跟踪，功率利用率相对会有所提高。为了满足这种要求，所设计的MPPT控制需要具备以下三个功能：

1）能够寻找到最大功率点；

2）当控制工作点在最大功率点时停止扰动跟踪；

3）外界条件改变时，能够识别出最大功率点的改变，并进行新一轮最大功率点跟踪。

实际上，利用上述的中心差分法寻找最大功率点时，由于中心差分法也存在截断误差，所以当式（6-38）条件满足数个采样周期后，即可认为是所寻找的工作点就是最大功率点。此时，停止有效的扰动跟踪，以避免不必要的振荡。

其中，ξ_mpp为误差阈值，ξ_mpp值的选择取决于所要求的灵敏度以及测量的信噪比。

另外，根据极值理论，在最大功率点处满足：

其中，R_mpp对应光伏电池在最大功率点工作时的电阻，G_mpp对应光伏电池在最大功率点工作时的电导。

为了判断最大功率点是否发生改变，首先定义如下方程

其中，e_R对应光伏电池当前工作点对应的电阻绝对误差，e_G对应光伏电池当前工作点对应的电导绝对误差，E_R、E_G分别是e_R、e_G在一个周期中采样次数为N_th情况下的平均值。

根据上述关系式，可以通过检测E_R或E_G的变化来判断最大功率点是否发生改变。当平均误差E_R或E_G的值超过特定的参考值时，控制系统即认为最大功率点发生改变，并开始预置新的一轮MPPT。在跟踪新的最大功率点过程中，在新的最大功率点以外应停止计算平均误差E_R或E_G，而当跟踪到新的最大功率点时，则更新R_mpp和G_mpp，并且将平均误差E_R或E_G置零，然后由式（6-43）、式（6-44）进行新一轮的判断。