光伏电池非线性特征及自寻优算法详解

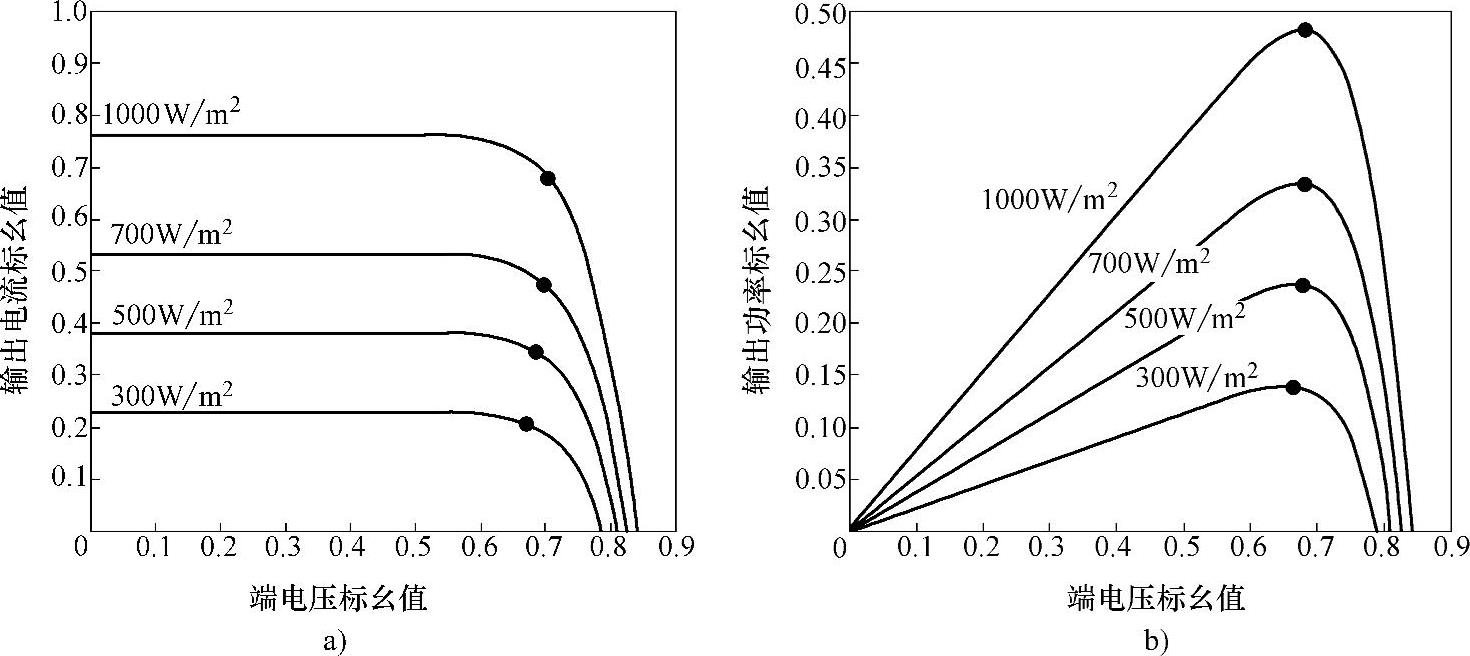
图6-1 相同温度而不同辐照度条件下光伏电池特性

a）U-I特性 b）P-U特性

在光伏发电系统中，光伏电池的利用率除了与光伏电池的内部特性有关外，还受使用环境如辐照度、负载和温度等因素的影响。在不同的外界条件下，光伏电池可运行在不同且唯一的最大功率点（Maximum Power Point，MPP）上。因此，对于光伏发电系统来说，应当寻求光伏电池的最优工作状态，以最大限度地将光能转化为电能。利用控制方法实现光伏电池的最大功率输出运行的技术被称为最大功率点跟踪（Maximum Power Point Tracking，MPPT）技术。

由2.3.1节给出的光伏电池的单二极管模型可知，一般在正常工作情况下，随辐照度和温度变化的光伏电池U-I和P-U特性曲线分别如图6-1、图6-2所示。显然，光伏电池运行受外界环境温度、辐照度等因素的影响，呈现出典型的非线性特征。一般来说，理论上很难得出非常精确的光伏电池数学模型，因此通过数学模型的实时计算来对光伏系统进行准确的MPPT控制是困难的。

图6-2 相同辐照度而不同温度条件下光伏电池特性

a）U-I特性 b）P-U特性

理论上，根据电路原理：当光伏电池的输出阻抗和负载阻抗相等时，光伏电池的输出功率最大，可见，光伏电池的MPPT过程实际上就是使光伏电池输出阻抗和负载阻抗等值相匹配的过程。由于光伏电池的输出阻抗受环境因素的影响，因此，如果能通过控制方法实现对负载阻抗的实时调节，并使其跟踪光伏电池的输出阻抗，就可以实现光伏电池的MPPT控制。为了方便讨论，光伏电池的等效阻抗R_opt被定义成最大功率点电压U_mpp和最大功率点电流I_mpp的比值，即R_opt=U_mpp/I_mpp。显然，当外界环境发生变化时，R_opt也将发生变化。但是，由于实际应用中的光伏电池是向一个特定的负载传输功率，因此就存在一个负载匹配的问题。

图6-3 光伏电池的伏安特性与负载特性的匹配

光伏电池的伏安特性与负载特性及其匹配的过程如图6-3所示，图中光伏电池的负载特性以一条过坐标原点的电阻特性直线表示。由图6-3可以看出，在辐照度1的情况下，电路的实际工作点正好处于负载特性与光伏U-I特性曲线的交点a处，而a点正好是光伏电池的最大功率点（MPP），此时光伏电池的伏安特性与负载阻特性相匹配；但在辐照度2的情况下，电路的实际工作点则处于b处，而此时的最大功率点却在a′处，为此，必须进行相应的负载阻抗的匹配控制，使电路的实际工作点处于最大功率点a′处，从而实现光伏电池的最大功率发电。

传统的MPPT方法依据判断方法和准则的不同被分为开环和闭环MPPT方法。

实际上，外界温度、光照和负载的变化对光伏电池输出特性曲线的影响呈现出一些基本的规律，比如光伏电池的最大功率点电压U_mpp与光伏电池的开路电压U_oc之间存在近似的线性关系等。基于这些规律，可提出一些开环的MPPT控制方法。本章6.2节将简要介绍基于输出特性曲线的开环MPPT方法，这一类方法简便易行，减少了工作点在远离最大功率点区域的MPPT时间，但对光伏电池的输出特性有较强的依赖性，只是近似跟踪最大功率点，效率较低，实际中常常和直接跟踪方法配合使用。(www.xing528.com)

闭环MPPT方法则通过对光伏电池输出电压和电流值的实时测量与闭环控制来实现MPPT，使用最广泛的自寻优类算法即属于这一类。典型的自寻优类MPPT算法有扰动观测法和电导增量法，这两种MPPT方法将在本章6.3节和6.4节中详细介绍。

从图6-1中不难看出，正常光照条件下光伏电池的输出P-U特性曲线是一个以最大功率点为极值的单峰值函数，因此，在最大功率点处有

自寻优类MPPT算法实际上就是通过自寻优控制，以使工作点满足式（6-1）条件。考虑到系统运行时的数字控制，实际中的式（6-1）条件常以ΔP/ΔU=0来近似取代。

无论扰动观测法还是电导增量法，实际中常采用对电压值进行步进搜索的方法，即从起始状态开始，每次对电压值做一有限变化（ΔU），计算前后两次的功率全增量（ΔP）的值。由于在同一搜索过程中，ΔU值一定且不为0，不论扰动的方向如何，系统总是朝ΔP为正值的方向搜索。当ΔP值足够小时，系统判定为最大功率点，从而实现自寻优控制。

扰动观测法使用的是前后两次连续采样点的绝对功率差来替代功率全增量（ΔP），如式（6-2）所示。

ΔP=P₂-P₁=U₂I₂-U₁I₁ （6-2）

电导增量法使用的是前后两次连续采样点的功率差分来代替功率全增量（ΔP），即用全微分的思想来线性近似出ΔP的值。如式（6-3）所示。

ΔP≈dP≈U₂（I₂-I₁）+I₂（U₂-U₁）=U₂ΔI+I₂ΔU （6-3）

由于自寻优类MPPT算法的理论是以光伏电池的输出P-U特性曲线是只有一个最大功率点的单峰值函数为依据的，而系统在实际工作中，当光伏电池被部分遮挡时，会出现原先的单峰值曲线畸变为多峰值的非正常情形（局部最大功率点），这样，对常规的自寻优类MPPT算法必须加以改进，本章的6.6节介绍了局部最大功率点情形时的MPPT方法及相关问题。

由于模糊控制理论和人工神经网络理论的不断发展和完善，智能控制在工业上的应用也越来越广泛。这一类控制尤其是人工神经网络控制的优点是不依赖于系统的模型，对各种工作情形均有较强的适应性。正是因为这一点，智能控制方法在最大功率点跟踪领域也开始占有一席之地。本章6.5节对这一类智能MPPT控制方法做了简要介绍。

为了使读者更好地理解最大功率点跟踪这一光伏发电领域的重要技术，本章的6.6节和6.7节对与最大功率点跟踪的一些相关问题也做了相应介绍。