同步旋转坐标系下单相并网逆变器控制优化

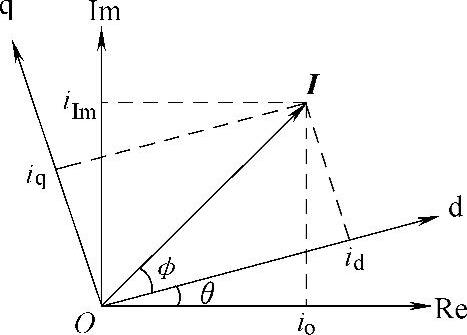
图5-63 虚拟矢量与坐标变换示意

上述单相并网逆变器的PR调节器控制虽然实现了电流的无静差控制，然而这种基于静止坐标系的控制却不便实现有功、无功功率的独立控制。但是，在三相并网逆变器的控制中，静止坐标系中三相对称的交流量通过坐标旋转变换即可变换成同步坐标系下的直流量，并利用简单的PI调节器控制不仅实现了电流的无静差控制，而且也实现了有功、无功功率的解耦控制。然而，要实现交流量的坐标旋转变换，至少需要具有两个自由度，例如两个正交的交流量。显然，单相系统只有一个自由度，无法直接进行坐标旋转变换，为此可虚拟出一个与单相系统实际交流量正交的交流量来满足坐标旋转变换的两个自由度条件，从而可以采用类似同步坐标系下三相并网逆变器的PI调节器控制，以实现电流的无静差跟随控制。实际上，如图5-63所示：只要在单相系统中将实际的交流量（例如输出电流i_o）延迟90°就可虚拟出一个正交分量i_Im，而将i_o和虚拟出的正交分量i_Im合成实际上构成了两相静止坐标系ReIm中的虚拟矢量I。将i_o、i_Im经同步旋转坐标系d-q轴分解，即可得到虚拟矢量I相应的d轴及q轴分量。具体分析如下：

若令单相并网逆变器的网侧电流i_o为

i_o=Icos（ω₀t+ϕ） （5-127）

式中 I——电流幅值；

ϕ——初始相角；

ω₀——基波角频率。

由于dq坐标变换需要两个正交变量，因此可以设计了一个全通滤波器将i_o移相90°得到一个虚拟的变量i_Im，即

i_Im=Isin（ω₀t+ϕ） （5-128）

将两相静止坐标系ReIm中实际及虚拟的变量i_o、i_Im经过坐标旋转变换后即可得到dq坐标系下的d、q轴变量i_d、i_q，即(www.xing528.com)

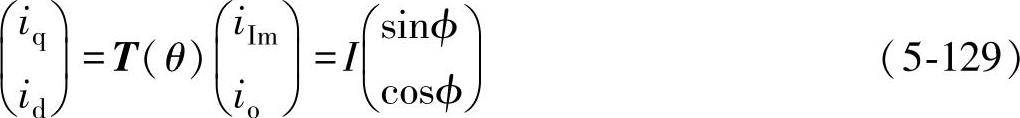
式中 T（θ）——ReIm-dq的坐标变换矩阵，且。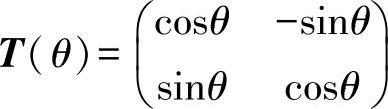

式（5-129）表明：在dq同步旋转坐标系中，虚拟矢量I被分解成i_d、i_q分量，其中：i_q表示有功电流分量，而i_d表示无功电流分量。与三相并网逆变器控制类似，对i_q、i_d进行独立的PI调节器控制，即可实现并网逆变器有功、无功功率的独立调节。

基于同步旋转坐标系单相并网逆变器的控制结构如图5-64所示。

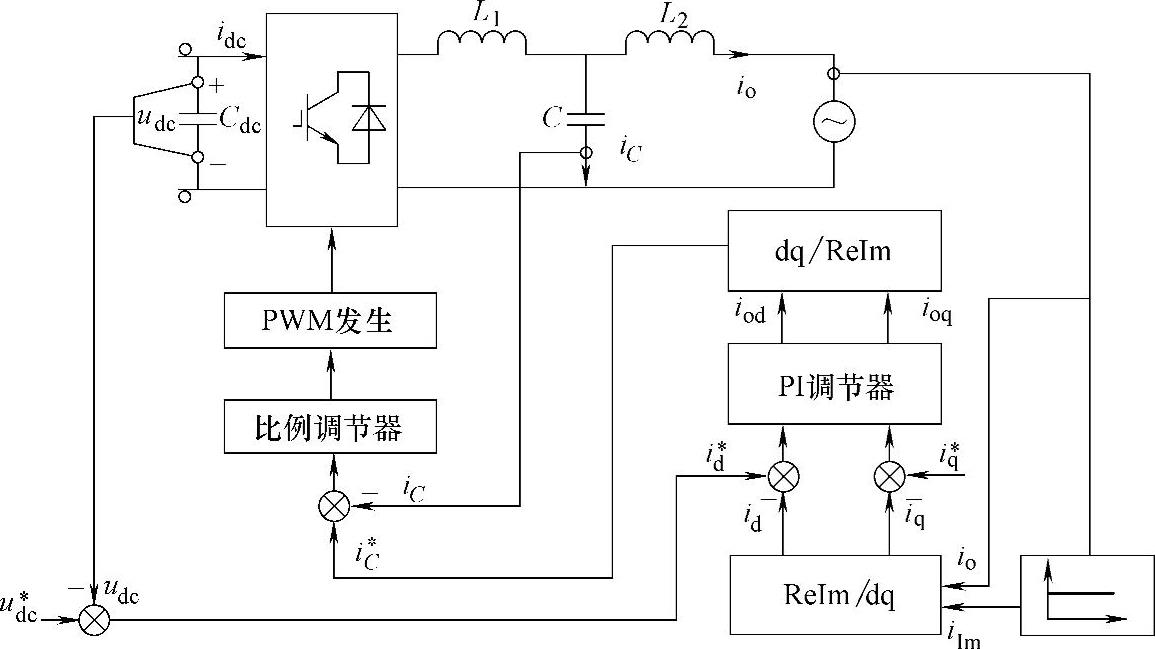
图5-64 基于同步旋转坐标系的单相并网逆变器的控制结构

控制系统采用了直流电压外环、功率电流环以及电容电流内环的三环控制策略，与上述采用PR调节器的单相有源逆变器控制方案相同，电容电流内环由于具有电容电压微分控制的特性，从而增加了控制系统的阻尼，抑制了系统振荡，提高了控制稳定性。

值得注意的是：基于同步旋转坐标系单相并网逆变器的控制，可以进行有功、无功电流i_q、i_d的独立控制，而i_q、i_d经PI调节器调节后相应的输出i_cd、i_cq还需进行相应的逆变换，即得到两相ReIm静止坐标系中的控制变量i_C^∗、i_Imc，即

通过dq-ReIm的坐标变换后，Im轴的虚拟变量i_Imc被略去，而Re轴的变量i_C^∗保留并作为电流内环反馈变量的给定量。由于电流内环无需实现无静差控制，因而只需采用P调节器。