静止坐标系下单相并网逆变器控制优化

1.基于PI、P调节器的双环控制策略

在中小功率单相并网逆变器中，其输出LCL滤波器的电容一般较小，因此可以考虑采用较为简单的双环控制策略，其系统及控制结构如图5-58所示。

图5-58中，并网逆变器的直流电压外环采用PI调节器，通过稳定直流侧电压实现逆变器输入、输出能量的平衡；电流内环的电流幅值参考值I_m^∗由直流电压外环调节器的输出给定，通过检测获得电网电压相位角θ，并由cosθ、I_m^∗的乘积获得瞬时输出电流的参考信号i_L^∗₁，电流内环一般可采用简单的P调节器，以实现电流的快速控制；为了抑制电网电压扰动，采用了电网电压前馈控制，电流环的输出与电网电压的前馈信号叠加后经过SPWM调制后输出驱动开关管，以实现单相逆变器的并网控制。

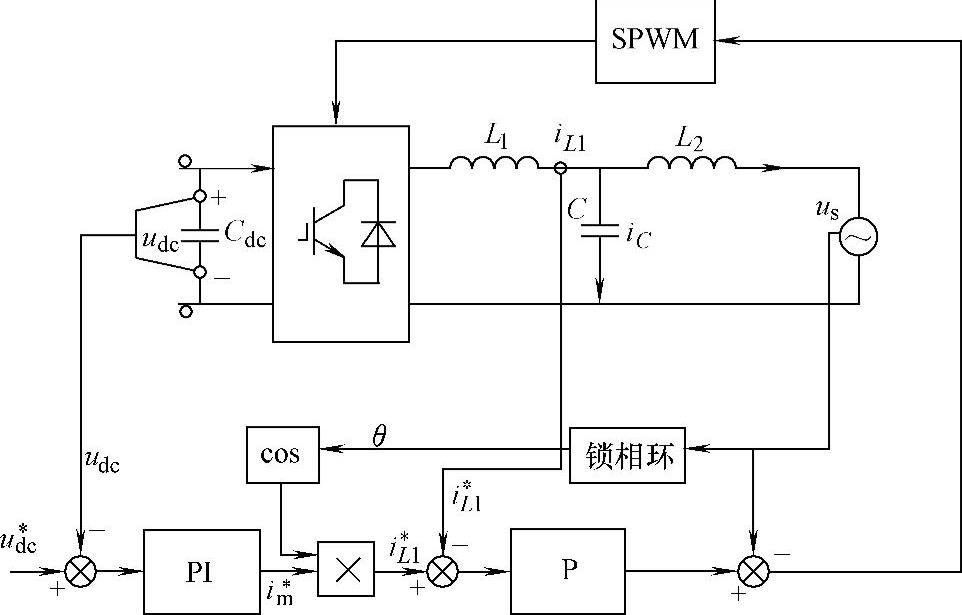
图5-58 基于PI、P调节器的单相并网逆变器的双环控制系统结构

2.采样基于比例谐振（PR）调节器的单相并网逆变器的多环控制

上述基于PI、P调节器的单相并网逆变器的双环控制虽然控制简单，但存在以下不足：

1）电流环无法实现电流的无静差控制；

2）当输出滤波器的电容较大时系统可能发生振荡；

3）由于没有直接控制网侧电流，因此会降低网侧电流品质。

为克服上述不足，可以采用基于比例谐振（PR）调节器的单相并网逆变器的多环控制策略。采用基于PR调节器的单相并网逆变器的多环控制结构如图5-59所示。

图5-59 采用PR调节器的单相并网逆变器控制结构

图5-59中，直流电压外环仍采用PI调节器控制，以稳定直流侧电压；电网电流环的电流幅值参考值I_m^∗由直流电压外环调节器的输出给定，通过检测获得电网电压相位角θ，并由cosθ、I_m^∗的乘积获得瞬时电网电流的参考信号i_L^∗₂，为实现电网电流的无静差控制，电网电流环可采用比例谐振调节器（PR）。为抑制LCL滤波器的振荡，图5-59中采用了电容电压微分即电容电流反馈控制，从而有效地增加了系统阻尼，电容电流内环采用P调节器控制，以保证内环控制的快速性；内环调节器的输出经过SPWM调制后驱动开关管，以实现单相逆变器的并网控制。

以下简单讨论比例谐振调节器（PR）的基本问题：

在静止坐标系中，若要实现正弦参考信号的无静差控制，根据内模定理，则要求在系统开环传递函数中包含正弦信号的s域模型，由于正弦信号可以是cos和sin两种形式表示，因此，正弦信号相应的s域模型可由以下两种无阻尼谐振的传递函数形式，即

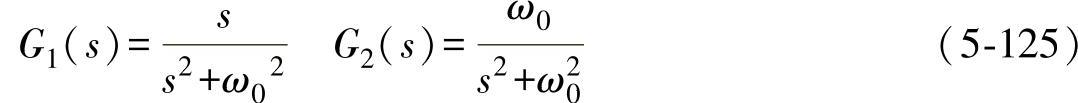(www.xing528.com)

为了比较两种传递函数特性，分别作出相应的博德图，如图5-60所示。

由图5-60不难看出：G₁（s）和G₂（s）在ω₀附近都具有无穷大的开环增益，因此可实现频率为ω₀的正弦信号的无静差控制。然而：G₁（s）的相角变化范围为90°～-90°，而G₂（s）的相角变化范围为：0°～-180°，可见，从稳定性的角度来看，G₁（s）的形式对系统稳定更有利，而G₂（s）可能使系统的相角裕度不足，从而引起系统的振荡。

上述分析表明：为实现对正弦信号的无静差控制，可以采用传递函数为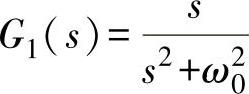形式的调节器设计，其博德图如图5-61所示。

另外，为了使调节器增加一个可控的自由度，以使得系统的闭环极点位置可以在根轨迹上自由配置，可在上述G₁（s）中增加一个可调的比例系数，则调节器的传递函数变为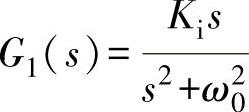，相应的G₁（s）博德图如图5-62所示。

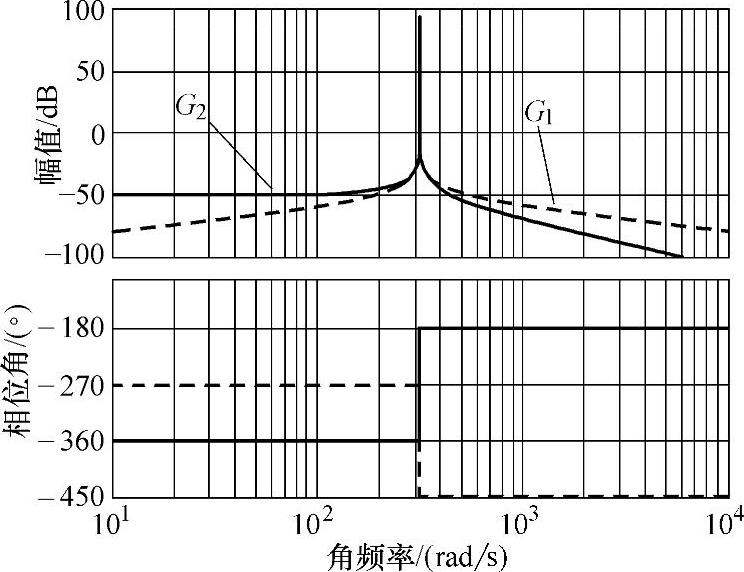
图5-60 G₁（s）与G₂（s）博德图比较

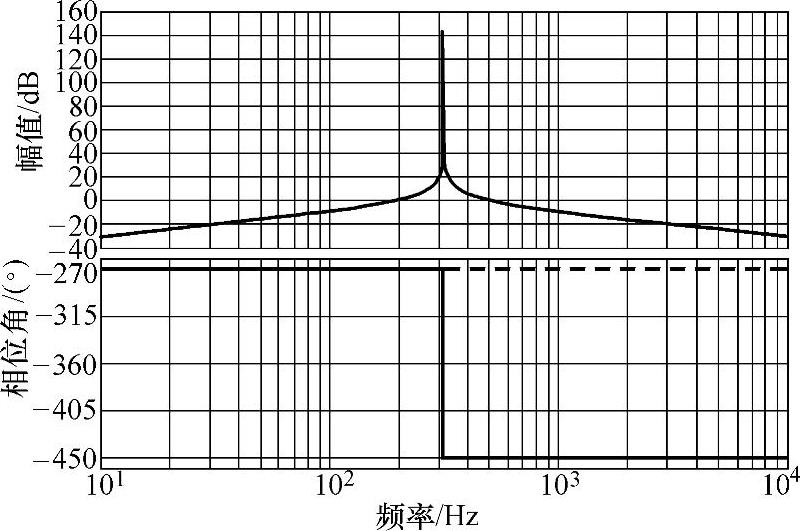
图5-61 调节器采用G₁（s）形式的博德图

图5-62 G₁（s）、G_c（s）博德图

从图5-62可以看出：当调节器采用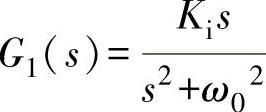的形式后，虽然系统在ω₀附近具有无穷大的开环增益，但在其他频率处，其增益呈衰减趋势。因而，为了补偿原有的增益呈衰减趋势，提高系统的动态性能，需要相应增大ω₀外频率处的开环增益，为此在原有传递函数基础上，引入比例项，即引入比例项的调节器传递函数为

G_c（s）的博德图如图5-62所示，与其中G₁（s）的博德图相比，G_c（s）的博德图在高频段对系统有较大的增益补偿，从而提高了系统截止频率，加快了系统的响应速度。

由于中既含有比例项，又含有谐振项，因此G_c（s）形式的调节器结构被称为比例谐振调节器或称PR调节器。

需要注意的是：因为比例谐振调节器是使系统在特定频率ω₀处获得无穷大的开环增益，因而其仅能无静差跟随给定信号频率ω₀时的正弦量，对于给定信号频率是变化量的场合是不适用的。