基于LCL滤波的并网光伏逆变器滤波器设计

由于采用LCL滤波器设计时，除了满足并网逆变器的网侧滤波特性（即满足网侧谐波电流含量要求）外，还应考虑：①使滤波电感和电容吸收的无功功率尽可能地小；②使逆变器桥臂侧电流谐波尽可能小；③使逆变器桥臂侧输出电压对网侧基波电流的控制能力尽可能大；④应使滤波器的谐振频率满足一定的控制要求。

总之，从并网逆变器的控制要求分析，并网逆变器LCL滤波器参数的选取主要可从以下3个方面进行考虑，即

1）满足有功功率、无功功率控制的要求；

2）满足电流跟踪响应的要求；

3）满足谐波电流指标的要求。

具体讨论在5.4.4.1中给出。

5.4.4.1 LCL滤波器参数的设计限制^[2，29-33]

LCL滤波器的参数设计，有如下4个限制条件：

（1）总电感量（L+L_g）的设计限制

从稳态条件下并网逆变器输出有功（无功）功率的能力考虑，并网逆变器LCL滤波器的总电感量（L+L_g）应予限制。考虑并网逆变器对有功和无功功率的稳态控制性能，稳态时LCL滤波器可等效为电感为L+L_g的L滤波器。由并网逆变器数学模型的分析可知，在稳态条件下并网逆变器的交流侧矢量关系如图5-52所示。

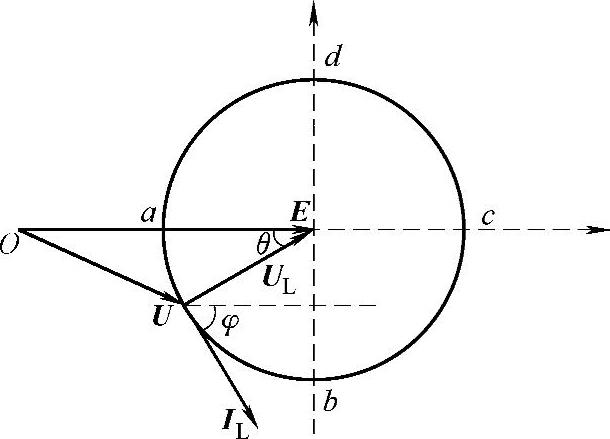
图5-52 稳态运行时网侧矢量图

E—网侧电压矢量 U—交流侧电压矢量 I_L—电感电流矢量 U_L—电感电压矢量

由图5-52不难看出，在电网电压矢量E不变的条件下，若适当选择电感和直流电压参数，即可控制并网逆变器运行在图5-52所示圆周的任意一点上，以在电感L取值一定为前提，电流大小不同对应着不同的圆周。通过a、b、c、d四点将圆周分成四个圆弧段，位于不同的圆弧段上时并网逆变器具有不同的运行状态，不同的运行状态对应于不同的工作电流，对电感的设计要求也不一样。研究表明^[2]：并网逆变器运行于c点时电感设计的上限值最小，而运行于a点时电感设计的上限值最大。设计时考虑最严重的情况，即工作在c点的情况，若采用SVPWM控制，则该情况下对电感设计的上限值为

式中 E_P——网侧电压的峰值；

I_LP——电感电流的峰值。

（2）滤波电容C_f的设计限制

在并网逆变器中，其LCL滤波器中的滤波电容值越大，产生的无功就越多，同时也降低了逆变器的功率变换能力。因此，在并网逆变器LCL滤波器的设计中，电容产生的无功一般被限制为不超过5%的系统额定功率，即有

3u²_CωC_f≤5%P_n （5-100）

式中 u_C——电容电压；

P_n——并网逆变器的额定功率。

若网侧电感上的压降相对较小时，则电容电压u_C可近似为电网相电压u_n，即u_C=u_n，因此有

（3）谐振频率f_res的设计限制

对于LCL滤波器，一般要求其滤波器的谐振频率设计在10倍基频和0.5倍开关频率之间，即有

10f_n≤f_res≤0.5f_sw （5-102）

式中 f_n——电网基频；

f_sw——并网逆变器调制的开关频率。

（4）无源阻尼电阻R_d的设计限制

当考虑LCL滤波器电容串阻尼电阻R_d时，其并网逆变器桥臂侧输出电压到网侧电流的传递函数为

显然，增大电阻R_d可提高系统阻尼，使系统更稳定，然而增大电阻会使损耗增加，即

P_d=3R_d∑[i（h）-i_g（h）]² （5-104）

可见，阻尼电阻R_d的设计需要在系统阻尼和损耗之间折中考虑。在LCL滤波器参数的工程设计中，阻尼电阻一般取值为谐振角频率ω_res处滤波电容C_f容抗的1/3，即

5.4.4.2 LCL滤波器桥臂侧电感L的选取

尽管并网变流器的谐波指标如IEEE519、IEEE929、IEC61000等所关注的是并网接入点的电流谐波和电压谐波^[34]，但就变流器本身的设计和控制而言，桥臂电流纹波也需要一定的限制。桥臂电流的纹波过大不仅会使滤波元件的损耗增大，而且还使功率开关管承受较高的开关应力，同时还会影响到并网逆变器的控制^[30，35]。因此并网逆变器采用LCL滤波时，即便网侧电流谐波满足并网要求，其桥臂侧电感的选取也不能过小，工程上通常要求把桥臂电流纹波限制在一定范围之内。以下根据并网逆变器桥臂侧电流纹波含量的要求设计桥臂侧电感的参数。

实际上，并网逆变器桥臂侧的电感电流是随开关周期而脉动的，为了限制电感电流纹波，需要分析并网逆变器输出的一个工频周期中不同时段内的电感电流纹波的变化规律。为此，需利用逆变器输出工频周期中不同时刻内的瞬态电感电流的数学关系来分析和求取电流纹波变化规律，并从中获得最大的电感电流纹波值，进而能通过电感值的设计将并网逆变器桥臂侧的电流纹波幅值限制在一定范围之内。

由于不同的并网逆变器电路拓扑和调制方式，其逆变器的输出瞬态电压波形也不尽相同。而对于基于LCL滤波的并网逆变器而言，其桥臂侧电感L较网侧电感L_g大，为简化分析，可以等效为单一的L滤波进行设计。因此，为分析问题方便，以下以图5-10所示的基于L滤波的SPWM调制的三相半桥无中线并网逆变器拓扑为例进行分析。

首先定义二值逻辑开关函数S_k为

以a相为例，其逆变器桥臂开关通、断时的回路方程为

其中，u_dc为直流侧电压，i_a为A相并网电流，u_a为a相电网电压，L为桥臂侧电感。

根据式（5-107）可知，a相电流的变化不仅取决于本相电网电压和开关状态的变化，还取决于b相和c相开关状态的变化。为此，将式（5-107）依据不同的开关状态分解得

根据式（5-108）可以得出电感电流的瞬时变化规律，以逆变器桥臂侧电流的基波分量过零处和峰值处为例，可得图5-53所示的电流波形。

观察图5-53可知，在对称的SPWM调制方式下，同一工频周期中的不同时段内，三相开关占空比变化的大小关系并不是惟一的，因此式（5-108）中描述的电感电流数学表达式也不是惟一的。为此根据其占空比变化规律，可以将电流变化分为几个不同的区间。由于在一个工频周期内，其稳态时逆变器输出的正负半周占空比对称，因此可以以半个周期进行区间划分，图5-54为其区间划分的示意图。

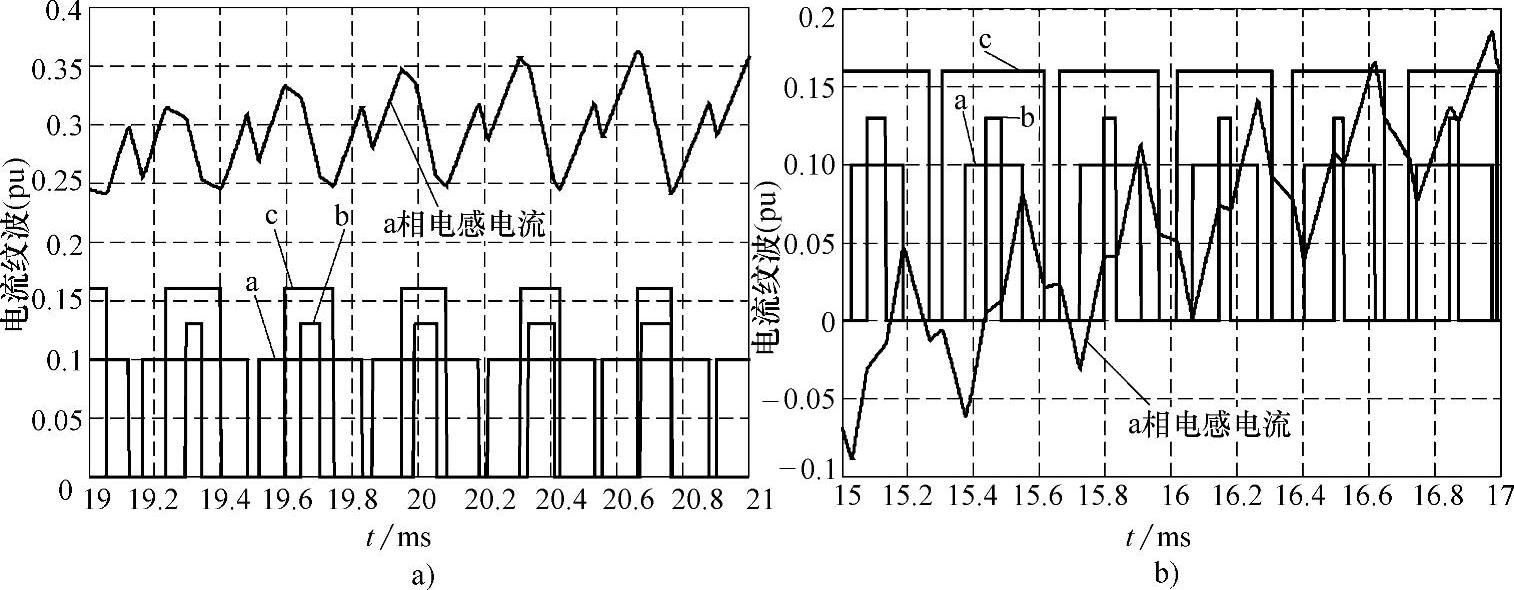
图5-53 不同占空比对应的电流纹波变化规律

a）桥臂输出基波电流峰值附近的电流纹波 b）桥臂输出基波电流过零附近的电流纹波

注：为了清楚比较分析a、b、c三相的开关占空比变化，图中，对a、b、c三相的占空比的幅值分别进行了不同尺度的描绘。图中横坐标为最小时间单位1μs的倍数。

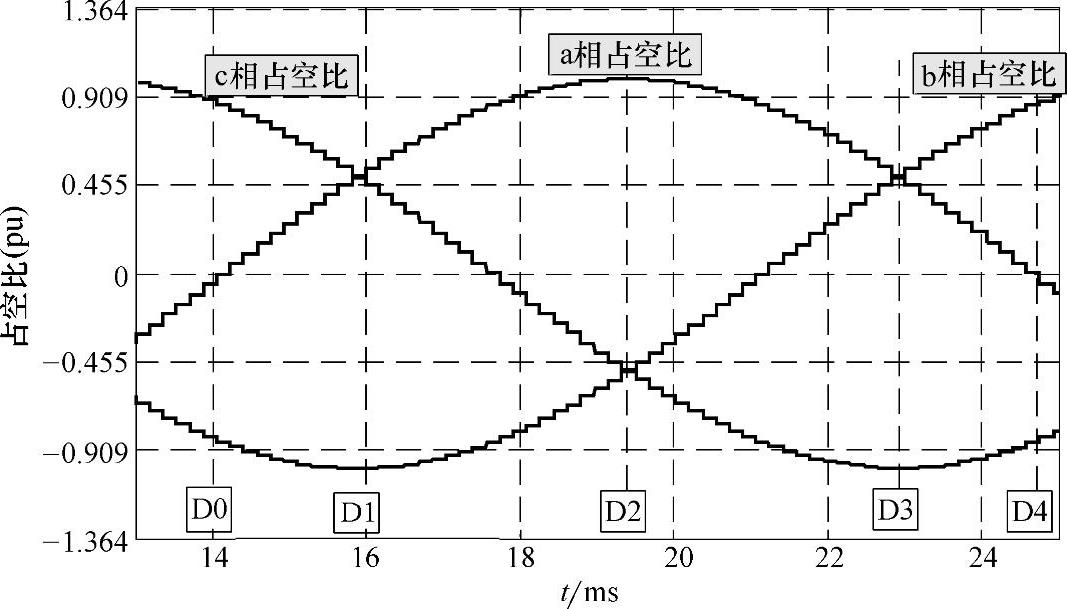
图5-54 占空比区间划分

从图5-54可以看出，4个占空比变化区间即（D0，D1）、（D1，D2）、（D2，D3）、（D3，D4）中，（D0，D1）与（D3，D4）是对称的，而（D1，D2）与（D2，D3）也是对称的，因此可以（D0，D1）、（D1，D2）区间为例来分析计算电流纹波幅值的变化规律。

考虑（D0，D1）区间的开关占空比变化规律，即：c相占空比最大，a相次之，b相最小。由此可进一步分析此区间内三相桥臂的开关状态关系，以a相为例：当a相上桥臂开关管开通时，由于c相占空比最大，将不存在S_b+S_c=0的状态；而当a相下桥臂开关管开通时，将不存在S_b+S_c=2的状态。

因此，在区间（D0，D1）内，式（5-108）可以简化为

其中，T_{on_a}、T_{on_b}、T_{on_c}为各相开关管的开通时间。

若要求得式（5-109）描述的电流纹波变化规律，需要研究一个开关周期T中各相开关管的开通时间T_{on_a}、T_{on_b}、T_{on_c}的变化规律。显然，当三相开关占空比分别记为D_a、D_b、D_c时，则有：T_{on_a}=D_aT，T_{on_b}=D_bT，T_{on_c}=D_cT。

由式（5-107）所描述的开关函数模型分析可知，三相半桥桥臂侧电压的瞬时值之和并不为零，这是由于开关函数模型反映了逆变器的高频瞬时特性。为了得到逆变器开关占空比的变化规律，需要分析逆变器的低频开关特性，当开关频率相对于工频足够高时，可以忽略开关函数模型中的高频分量，则开关函数模型的低频数学模型可表示为

S_a≈0.5+0.5msinθ_a

S_b≈0.5+0.5msinθ_b （5-110）

S_c≈0.5+0.5msinθ_c

其中，m=2u/u_dc，u为交流侧电网电压峰值。

由于稳态时并网逆变器各相开关管的占空比变化规律为(www.xing528.com)

D_a=0.5+0.5msinθ_a

D_b=0.5+0.5msinθ_b （5-111）

D_c=0.5+0.5msinθ_c

显然，只要将开关函数模型中的开关函数以占空比取代，即可获得相应的低频模型。将式（5-110）带入式（5-107）得

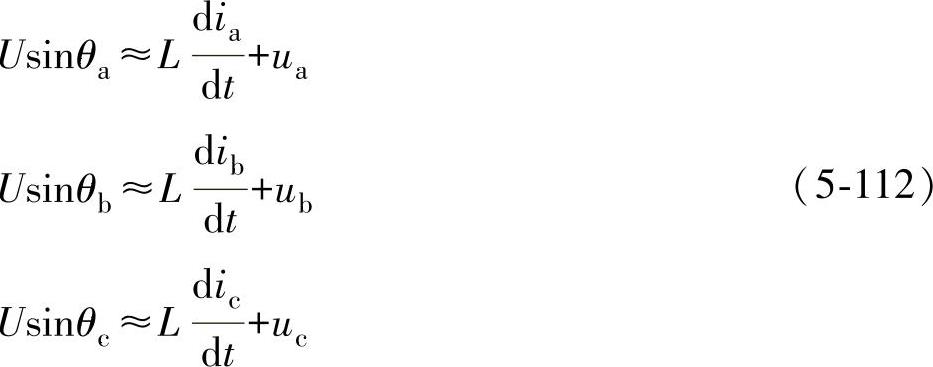
这里，由于低频情况下电感的压降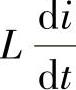远小于电网电压u，因此，占空比函数的相位θ_a、θ_b、θ_c可以近似认为和各相电网电压相位角相同。值得注意的是，为了补偿这部分近似误差，最后对计算出的电感大小应留有一定的裕量。

这样，根据式（5-109）、式（5-111）和式（5-112）即可计算电流纹波幅值。取（D0，D1）区间开关周期T中电感电流的上升过程来计算a相电流的纹波幅值Δi_a关系，可得

同理，可求得（D1，D2）区间的a相电流纹波幅值Δi_a关系为

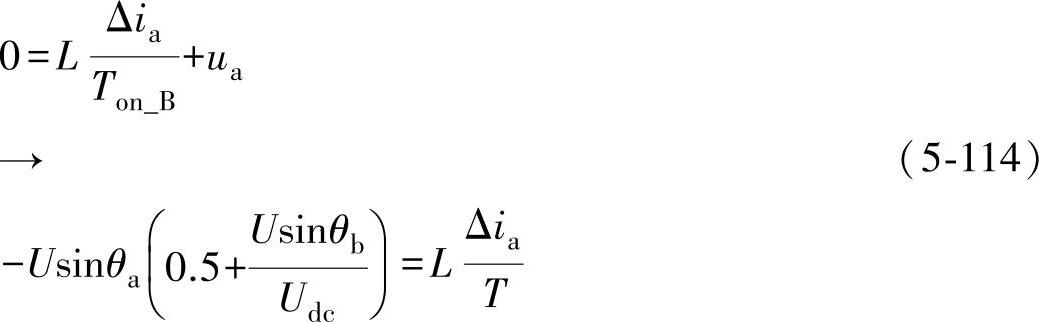
根据式（5-113）和式（5-114）计算可得a相电流纹波幅值Δi_a为

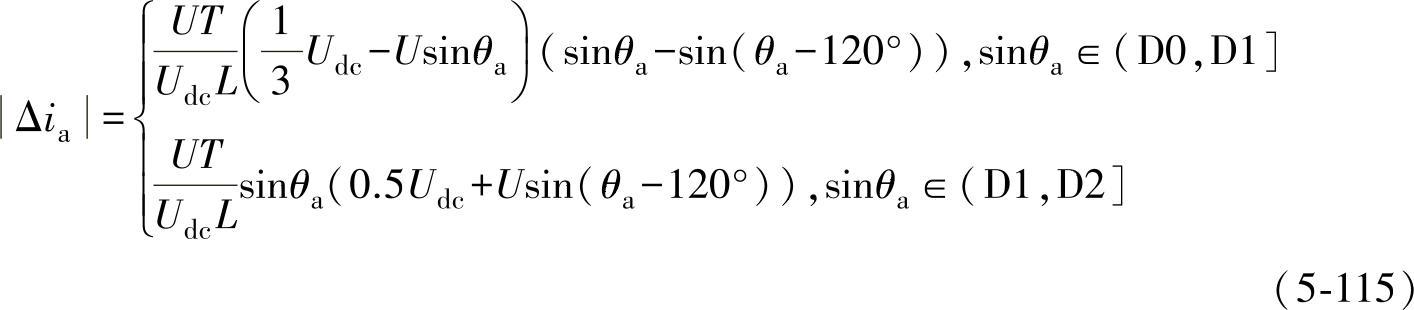
图5-55 电流纹波幅值随电网电压的变化规律

在半个工频周期内，电流纹波幅值随θ_a即电网电压的变化规律示意图如图5-55所示。

从图5-55看出，若忽略逆变器输出电感的低频压降，则在电网电压过零和峰值处，其开关电流纹波幅值最大。

在电网电压过零点处，θ_a=0°，根据式（5-115）可得电流纹波的幅值关系为

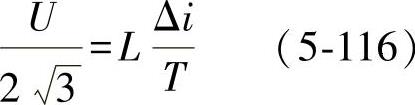
在电网电压峰值处，θ_a=90°，根据式（5-115），电流纹波的幅值关系为

针对式（5-116）和式（5-117），讨论如下。

1.电感参数与开关频率的关系

其他参数不变的情况下，开关频率越高，电感越小。

2.电感参数与交直流电压比值的关系

假定开关频率固定，当U/U_dc比值不同时，基波电流峰值处和过零处的电流纹波随U/U_dc的变化规律如图5-56所示。

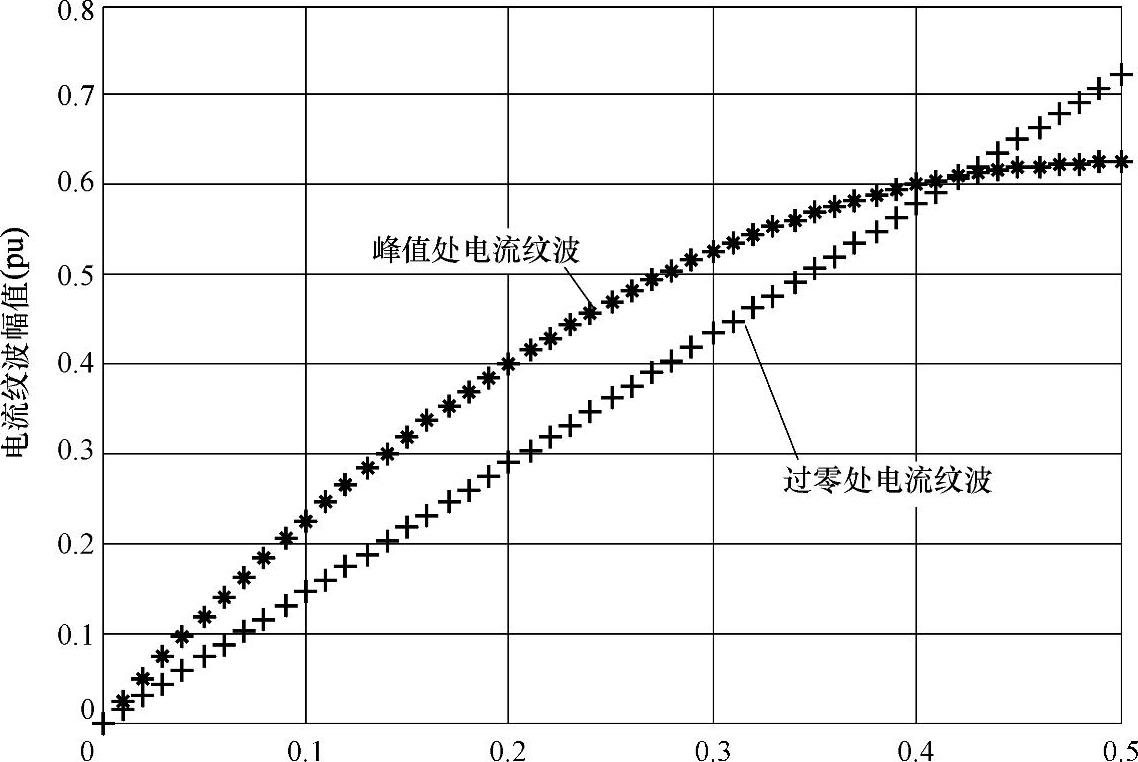
图5-56 电流纹波随U/U_dc的变化规律

从图5-56可以得出如下结论：

1）随着交直流侧电压比值的变大，电流纹波幅值逐渐变大，因此，对于相同的直流侧电压，网侧电压较小时电流纹波幅值相对较小；

2）当U/U_dc＜0.42时，基波电流峰值处的电流纹波幅值较大；

3）当U/U_dc≥0.42时，基波电流过零处的电流纹波幅值较大；

4）当U/U_dc=0.5时，电流纹波幅值最大，且最大值为。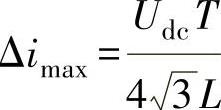

根据上述结论和并网逆变器桥臂电流控制中对最大电流纹波幅值Δi_max的要求，可按照上述结论4）中的最大电流纹波幅值设计相应的电感值，即

考虑到并网逆变器的运行效率和电感的成本，电感设计时应尽量小，另外考虑到上述近似计算所造成的偏差，因此在电感设计时其取值应留有一定的裕量。

5.4.4.3 LCL滤波器网侧LC参数的选取

在初选并网逆变器桥臂侧电感L参数后，可令网侧电感L_g的大小为

L_g=γL （5-119）

式中 γ——网侧电感比例系数。

若令x为滤波电容吸收的无功功率占系统功率的百分比值，则有

C=xC_b （5-120）

其中，x≤5%，而标幺值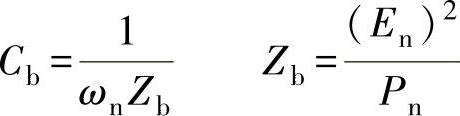

设计时，先按照5%的百分比算出电容最大值，而电容初选值一般可选择为此最大值的一半。

在初步选定了电容值和并网逆变器桥臂侧电感值后，接下来就是需要确定系数γ以得到网侧电感值，分析如下：

图5-57所示为h次开关频率谐波电流下等效的单相LCL滤波器结构，在高频状态，逆变器是一个谐波发生器，网侧相当于短路。i（h_sw）、u（h_sw）分别表示逆变器侧h次谐波电流和谐波电压，i_g（h_sw）表示网侧h次谐波电流，且图中u_g（h_sw）=0。由图5-57所示可推导出：

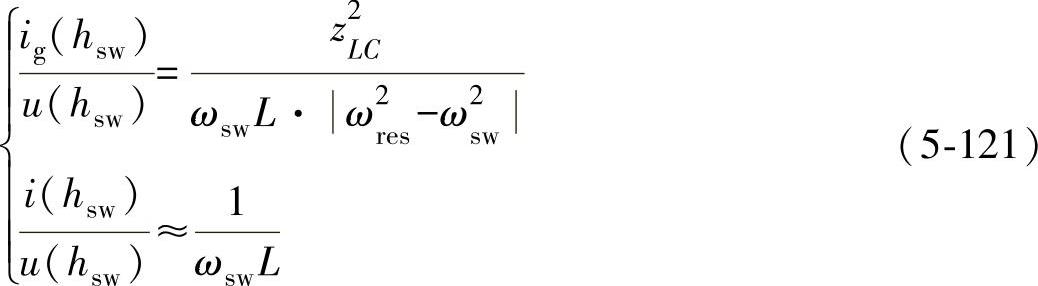
图5-57 h次开关频率谐波电流下等效的单相LCL滤波器结构

因此，从并网逆变器桥臂侧到网侧的电流谐波衰减表达式为

其中，z²_LC=[L_gC_f]^-1，ω²_res=（L_g+L）z_L²C/L，ω²_sw=（2πf_sw）²，f_sw是开关频率，h_sw=ω_sw/ω_n是开关谐波次数。

联立式（5-119）～式（5-122），得到脉动电流衰减与网侧电感比例系数γ之间的关系式为

其中，a=LC_bω²_sw是常值。

选择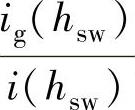的值，可确定系数γ，从而由式（5-123）即可得网侧电感值。通常一般初选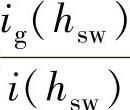值在20%左右。

5.4.4.4 LCL滤波器参数设计的检验与校正

1.总电感量（L+L_g）的检验与校正

由上面步骤，可依次算出LCL并网逆变器桥臂侧电感值L、电容值C_f以及网侧电感值L_g，此时，需要代入限制条件（1）即检验。若不满足此条件，需另行选择脉动电流衰减值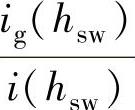，从而得到新的系数γ以及网侧电感值L_g。通过式（5-120）知，重新选择滤波电容无功功率的比例值也可达到类似的效果。直至满足限制条件（2）的要求，即满足。

2.谐振频率f_res的检验与校正

由式（5-103）传递函数可得到LCL滤波环节谐振频率的表达式，即

由初步得出的网侧电感值L_g、电容值C_f、并网逆变器桥臂侧电感值L检验得出的谐振频率f_res=ω_res/2π是否满足限制条件（3），即10f_n≤f_res≤0.5f_sw。

若不满足条件，再次重新选择脉动电流衰减值或滤波电容无功功率的比例值，以得出新的L_g、C_f和L值，直至满足限制条件（3）的要求。

3.阻尼电阻的确定

阻尼电阻值一般取为谐振点电容阻抗的1/3，即按照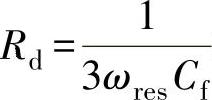求得即可。