使用有源阻尼法进行信号抑制

由上一节分析不难看出，通过增加阻尼电阻能够有效抑制LCL滤波器的谐振，有利于控制系统的稳定性，但是阻尼电阻的增加一方面还是有可能会影响谐波的滤波性能，另一方面也会增加系统损耗，降低系统效率，尤其是在大功率场合，阻尼电阻发热严重。

为了在不增加系统损耗的前提下，有效增加系统阻尼，抑制系统谐振并提高控制系统运行的稳定性，以控制取代实际阻尼电阻的有源阻尼控制策略引起了学术界的关注。所谓有源阻尼，就是无需实际的阻尼电阻，而是通过系统的控制算法来实现阻尼作用的方法。这种有源阻尼控制的基本思想可以从图5-33所示的博德图上加以解释，即当原系统博德图出现正谐振峰时，可以利用算法产生一个负谐振峰与之叠加，从而抵消和抑制原系统博德图的正谐振峰，以此增加系统阻尼。

显然，有源阻尼控制只是通过算法增加系统阻尼，没有附加阻尼电阻，因此没有增加损耗，从而提高了系统效率。然而，有源阻尼控制一般需要增加电压或电流传感器、并且控制系统结构相对复杂，这在一定程度上限制了有源阻尼的应用。但出于提高系统效率的考虑，有源阻尼有逐步取代无源阻尼的趋势和潜力。

有源阻尼法可分为虚拟电阻法、陷波器校正法^{[22，23，28]}和双带通滤波器法等^[24，25]，分别讨论如下。

1.虚拟电阻法^{[18，20，21]}

Pekik Argo Dahono首先提出了以“虚拟电阻”控制算法来替代实际阻尼电阻^[20]的有源阻尼控制，即虚拟电阻法。其基本思想就是将无源阻尼控制结构图进行等效变换，并以控制算法代替实际的无源阻尼电阻。下面以通常应用的电容支路串联电阻的无源阻尼结构为例来导出相应的虚拟电阻法控制系统结构。电容支路串联电阻的LCL并网逆变器电流环控制结构如图5-34所示。

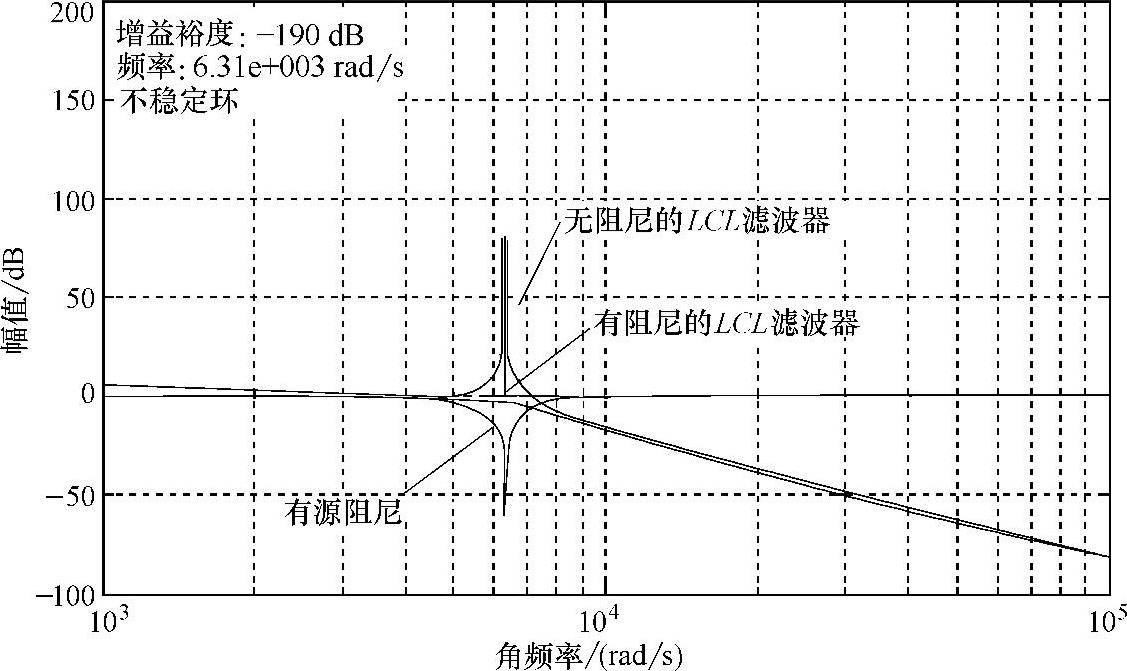
图5-33 有源阻尼原理示意图

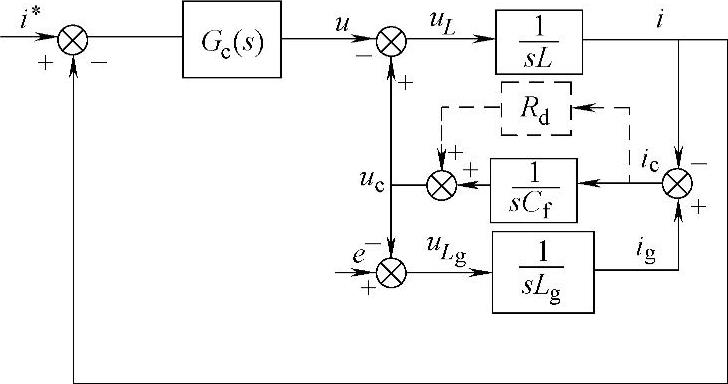
图5-34 电容支路串联电阻的LCL并网 逆变器电流环控制结构

其中，G_c（s）为电流环控制器的传递函数，根据自控原理中系统结构等效变换规则，可将图5-34变换如下，即

图5-35所示的等效结构表明，电容支路串联电阻的无源阻尼控制结构相当于在原有无阻尼结构的基础上多了一个阻尼电流分量i_csC_fR_d，而该阻尼电流分量实际上也可以通过在电流控制器的输入端利用算法加以实现，从而达到有源阻尼控制的目的，如图5-36所示。

图5-35 电容支路串联电阻控制的等效结构变换

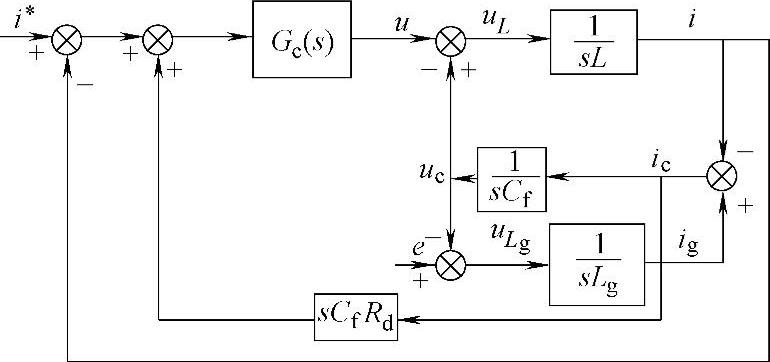
图5-36 虚拟电阻等效的有源阻尼控制结构

根据这种思想，可以设计出基于虚拟电阻法（电容串联电阻）的LCL并网逆变器有源阻尼控制结构，如图5-37所示。

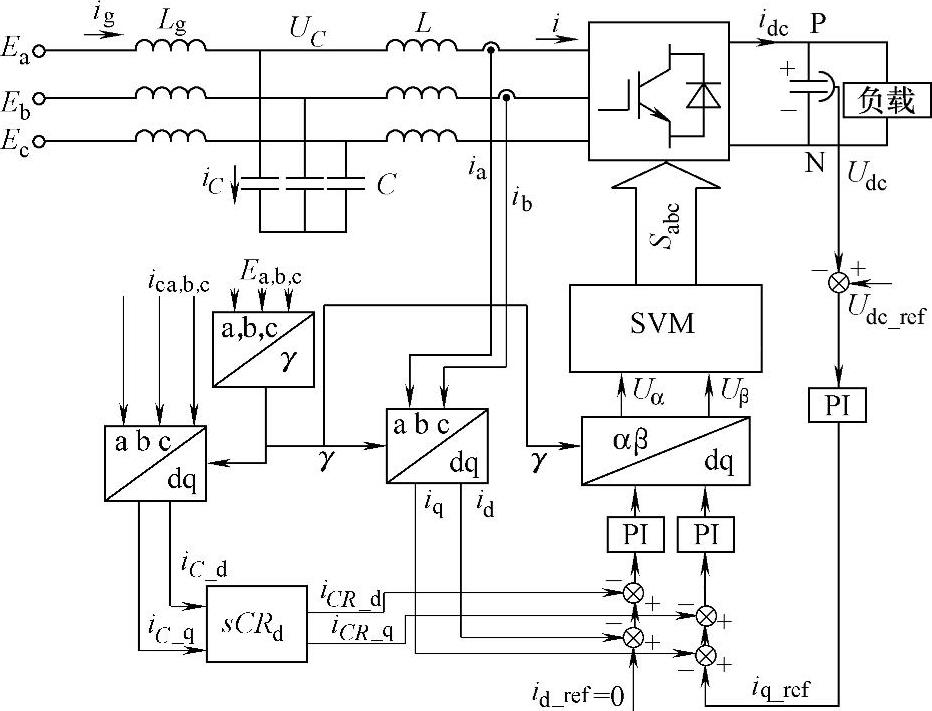
图5-37 基于虚拟电阻法的LCL并网逆变器有源阻尼控制结构图

这种控制结构的思想是检测LCL滤波器电容支路的电流i_C，并与sCR_d相乘后叠加到电压外环的输出电流指令上，然后经PI调节器实现有源阻尼控制。

下面对上述虚拟电阻法进行频率特性分析，首先将图5-36所示的控制结构简化，如图5-38所示。

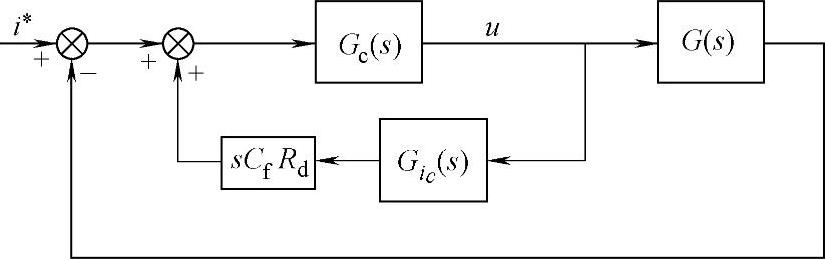
图5-38 虚拟电阻法控制结构的简化

其中，

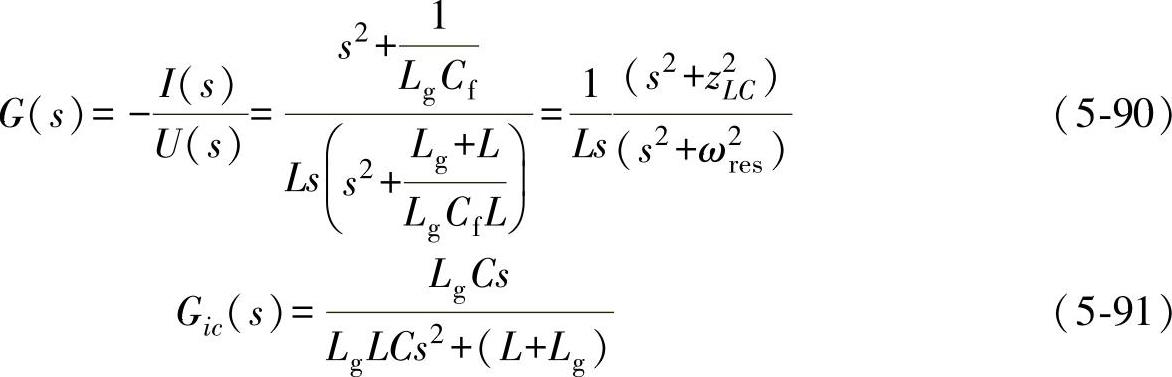
根据图5-34和图5-38以及式（5-90）、式（5-91）可以画出控制系统的开环博德图，如图5-39所示。

从图5-39可以看出，无阻尼控制方案在谐振频率处产生一个谐振峰；当采用无源阻尼电阻控制时，原谐振频率处的谐振峰得到极大的衰减，远小于0dB；而采用虚拟电阻法控制时，系统在谐振频率处的增益也在0dB之下，谐振峰也得到较大的衰减。值得一提的是，电容串联电阻的阻尼控制并不改变系统的低频和高频特性，因而系统的控制和滤波特性基本不受影响。

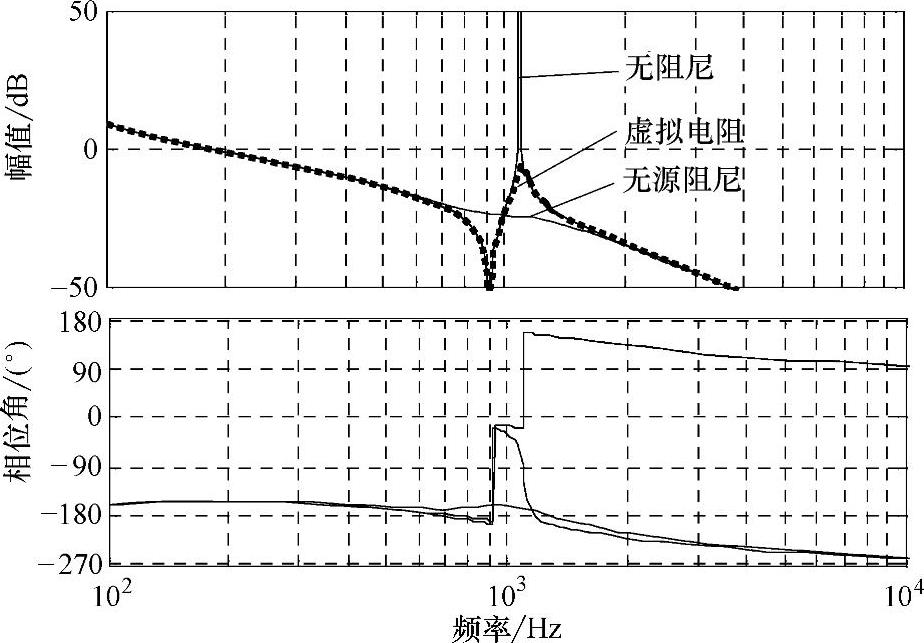
图5-39 虚拟电阻法博德图及其比较

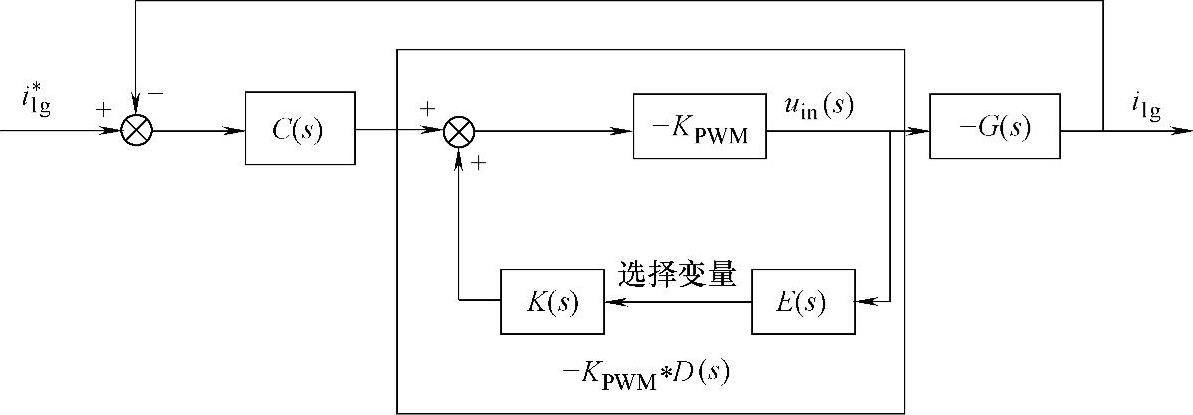
图5-40 陷波器结构有源阻尼算法结构简图

然而，从图5-39还可以看出，由于控制器结构及控制带宽的局限性，因此，从控制响应上，此种虚拟电阻的有源阻尼控制方案并不能完全等效于相应的无源阻尼方案。

另外，由于控制结构图节点等效变换的路径不只局限于一种，因此不同的等效方法可以得到不同的虚拟电阻控制算法。

2.陷波器校正法

实际上，为了实现阻尼控制，可以在控制系统中构造一个具有负谐振峰特性的环节，并以此抵消LCL滤波器产生的正谐振峰。由于陷波器具有这种负谐振峰特性，因此可以通过控制结构的设计，将陷波器特性引入系统控制中，这便是基于陷波器校正法的有源阻尼控制策略的基本思路。那么，如何进行系统结构设计，将陷波器特性引入系统控制呢？仍从LCL并网逆变器电流环出发进行讨论。实际上，如图5-40所示，可以通过电流环前向通道中引入适当的变量反馈，并将变量反馈构成的闭环环节（如图5-40中方框所示）整定为陷波器特性，就可以实现基于陷波器校正的LCL并网逆变器的有源阻尼控制。图5-40中D（s）即为构造的陷波器有源阻尼环节。

对于LCL并网逆变器而言，可以看出系统中可供选择的反馈变量有5个：网侧电感电压u₂（s）、滤波电容电压u_C（s）、滤波电容电流i_C（s）、逆变器桥臂侧电感电压u₁（s）、逆变器桥臂侧电感电流i₁（s）。图5-40中E（s）为u_in（s）到所选反馈变量的传递环节，即

[u₂（s）u_C（s）i_C（s）u₁（s）i₁（s）]^T=E（s）u_in（s） （5-92）

不同反馈变量选择所对应的各环节传递函数为

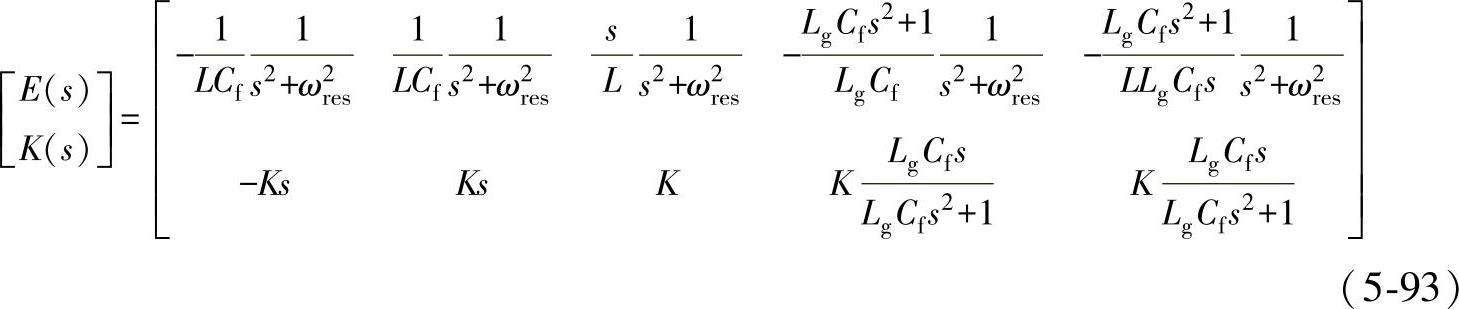
其中，K（s）是不同反馈变量所对应的陷波器的配置函数。

显然，为了消除图5-40中G（s）位于ω_res处的正谐振峰，可以将D（s）构造成陷波器结构，使得D（s）在谐振点ω_res处产生一个负的谐振峰，因此需要构造的陷波器传递函数D（s）如下：

式中 Q——陷波器的品质因数。

陷波器D（s）的博德图如图5-41所示，显然，在频率ω_res处，其增益为0，而对于偏离ω_res的信号，由于s²+ω²_res远大于Qs，其增益为1。

可见，图5-40中陷波器配置函数D（s）的构造依赖于反馈变量的选择，对于不同的反馈变量，所需要的配置函数K（s）也就不同。

从式（5-92）中可以看出，当选用u₂或者u_C作为反馈变量时，需要将K（s）配置成微分环节；当选用u₁或者i₁作为反馈变量时，需要配置的K（s）较为复杂，而且配置参数和系统参数有关；当选用i_C作为反馈变量时，只需要将K（s）配置成一个比例环节，且不受系统参数影响，可以很好地实现陷波器结构的有源阻尼算法。以下分别研究以u_C和i_C为反馈变量时的陷波器校正有源阻尼法的实现。

（1）以u_C为反馈变量时的陷波器校正有源阻尼法的实现

以上分析表明，当选用u_C作为反馈变量时，需要将K（s）配置成微分环节。而微分环节实现困难，且易引入噪声，为此可以采用超前-滞后环节代替微分环节的实现思路。超前-滞后环节的表达式为

其中，α＜1。(www.xing528.com)

根据式（5-95）可以画出超前-滞后环节的博德图，如图5-42所示。

图5-41 陷波器的基本博德图

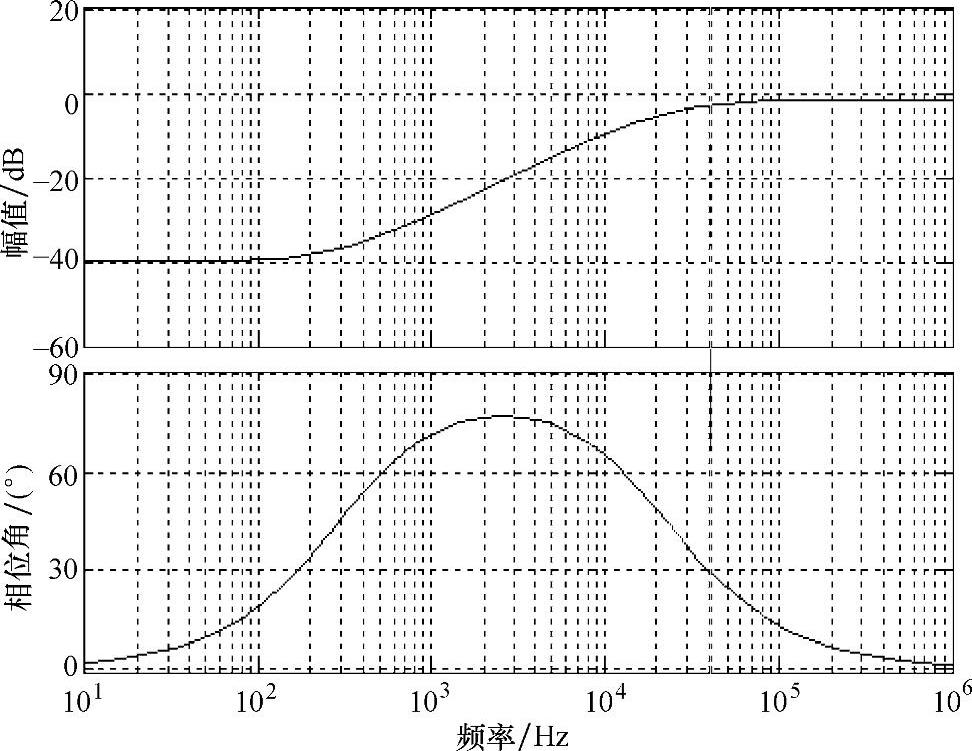
图5-42 超前-滞后环节的博德图

可见，从超前-滞后环节的博德图可以看出超前-滞后环节的基本特征^[24]：

1）其幅频特性类似于高通滤波器，具有选频特性。

2）其相频曲线具有正的相移。在、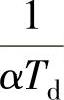之间的频段，超前-滞后环节对输入信号具有明显的微分作用，因此输出信号比输入信号超前，系统的相位裕度增加，且随着增大，微分效应越强，当频率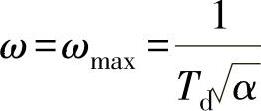时，最大超前角为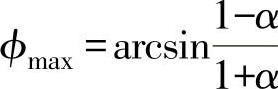，如图5-43a所示。

3）低频段的增益会下降，因而需要附加增益，以抵消低频段的增益下降。

4）超前-滞后环节具有高通特性，因而抗高频干扰的能力比较弱，所以K_d取值不能太大，如图5-43b所示。

图5-43 超前-滞后环节随参数变化的对数频率特性

a）不同α对应的超前-滞后环节频率响应 b）不同K_d对应的超前-滞后环节频率响应

在本系统设计中，将超前-滞后环节串联在电容电压反馈检测通道中，然后将输出值叠加到电流调节器输出，从而实现以u_C为反馈变量的基于陷波器校正法的有源阻尼控制，其控制结构如图5-44所示。

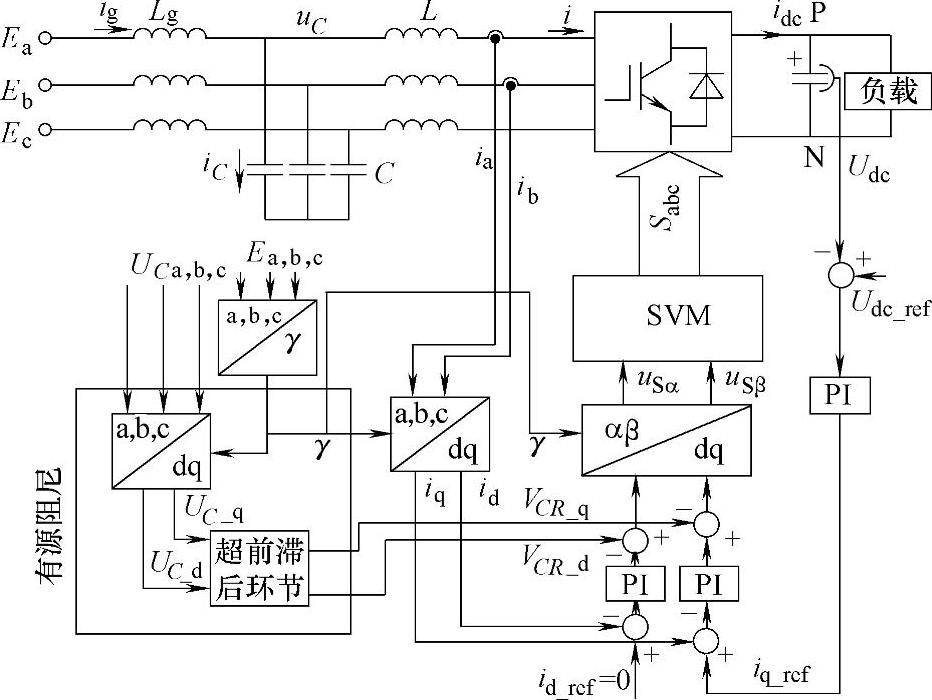
图5-44 以u_C为反馈变量的基于陷波器校正法的有源阻尼控制

根据以上分析，可以画出带有源阻尼的电流内环控制结构^[2，7]，为图5-45所示。

图5-45可以进一步简化为图5-46。

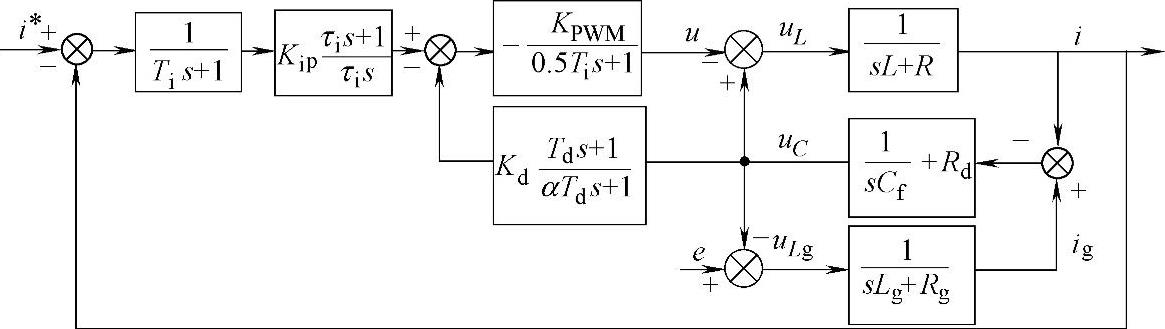
图5-45 基于超前-滞后网络的电流内环控制结构图

图5-46 基于超前-滞后网络的电流内环简化控制结构图

其中，

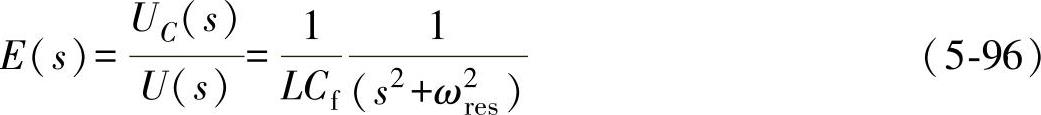
则图5-46中点画线框中所示的陷波器环节的表达式可以写为

建立上述关系式，画出D（s），G（s）以及D（s）G（s）的博德图，如图5-47所示。

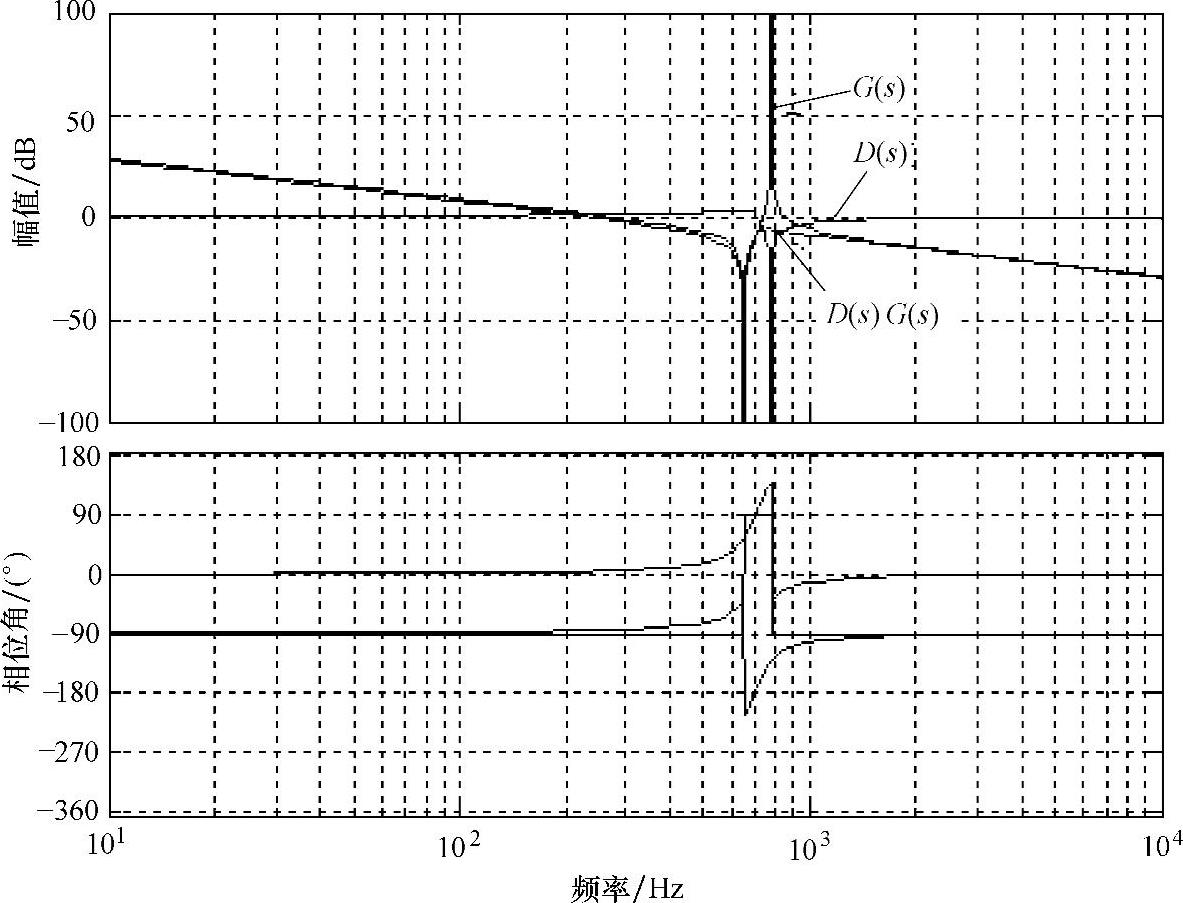
图5-47 D（s）、G（s）、D（s）G（s）的博德图及其对比

显然，由于超前-滞后环节的引入，使系统前向控制通道中构成了一陷波器环节D（s）。这一环节由于在低频阶段和高频段满足D（s）=1，因而对电流环性能没有影响，而在谐振频率附近，D（s）引入了与G（s）的正谐振峰相抵消的负谐振峰，从而有效地增加了系统阻尼。由于存在检测电容电压的需要，有必要在系统中额外增加电压传感器。

（2）以i_C为反馈变量时的陷波器校正有源阻尼法的实现

以上分析表明，当选用i_C作为反馈变量时，只需要将K（s）配置成一个比例环节，且不受系统参数影响，可以较方便地实现基于陷波器校正的LCL并网逆变器的有源阻尼控制，系统控制结构图如图5-48所示。

根据图5-48可以得出以i_C为反馈变量的基于陷波器校正法的有源阻尼控制框图，如图5-49所示。

图5-48 以i_C为反馈变量的基于陷波器校正法的有源阻尼控制结构图

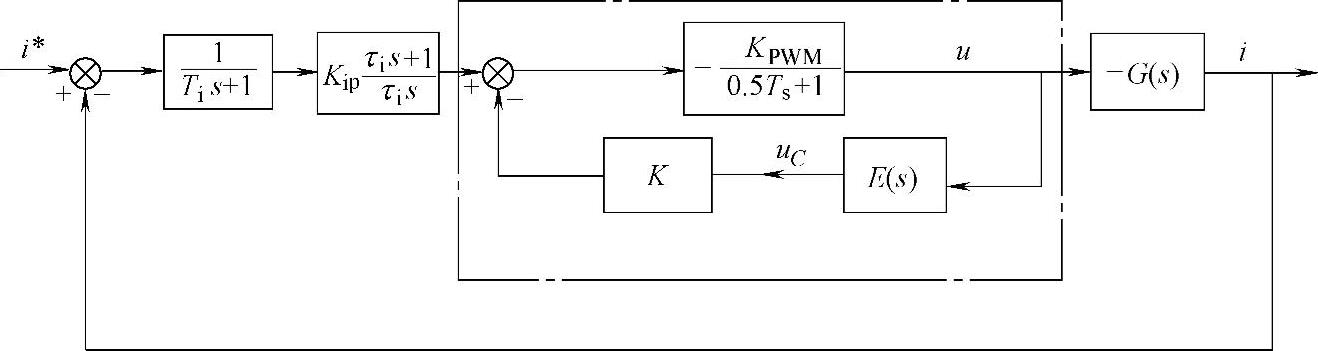
图5-49 以i_C为反馈变量的基于陷波器校正法的有源阻尼控制框图

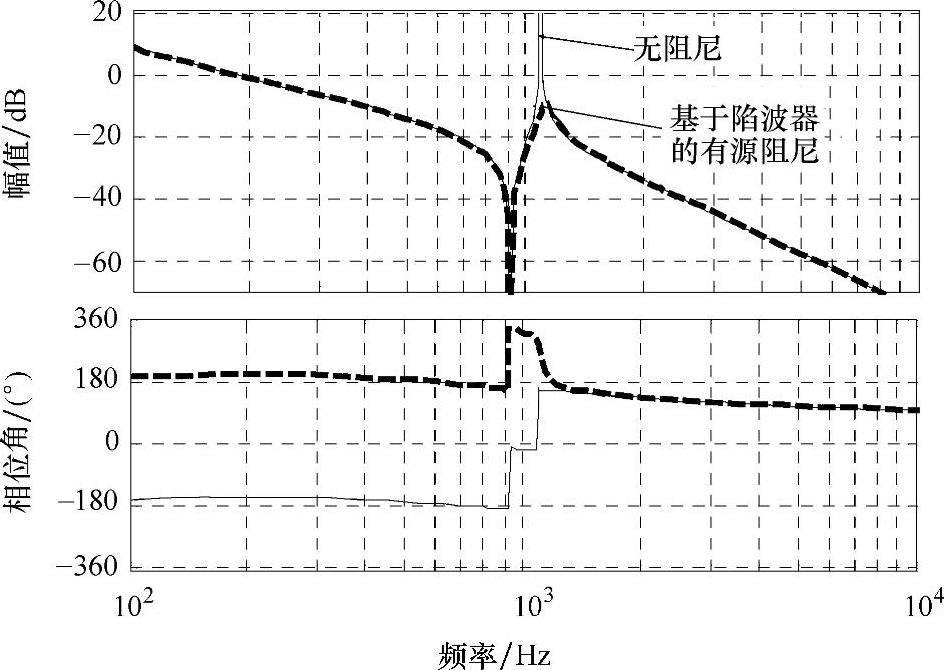
图5-50 有、无有源阻尼控制时的电流内环开环博德图

其中，K为比例配置系数，。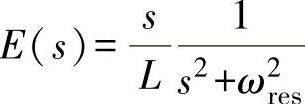

根据图5-49可以得出系统有、无有源阻尼控制时的开环博德图，如图5-50所示。

根据图5-50可以看出，基于陷波器校正的有源阻尼可以有效地抑制系统的谐振，增加系统阻尼。

3.双带通滤波器法

以上介绍的有源阻尼方法都需要附加额外的传感器，并且通过反馈环构建相应的陷波器环节，实际上可以在电流环控制器的输出直接通过算法增加陷波器环节，而不需要增设额外的传感器^[24]。然而简单的陷波器在高频时会引入相角偏移^[25]，因而一般可以采用带通滤波器来构建陷波器，这就是所称的基于双带通滤波器的有源阻尼控制，其控制结构如图5-51所示。

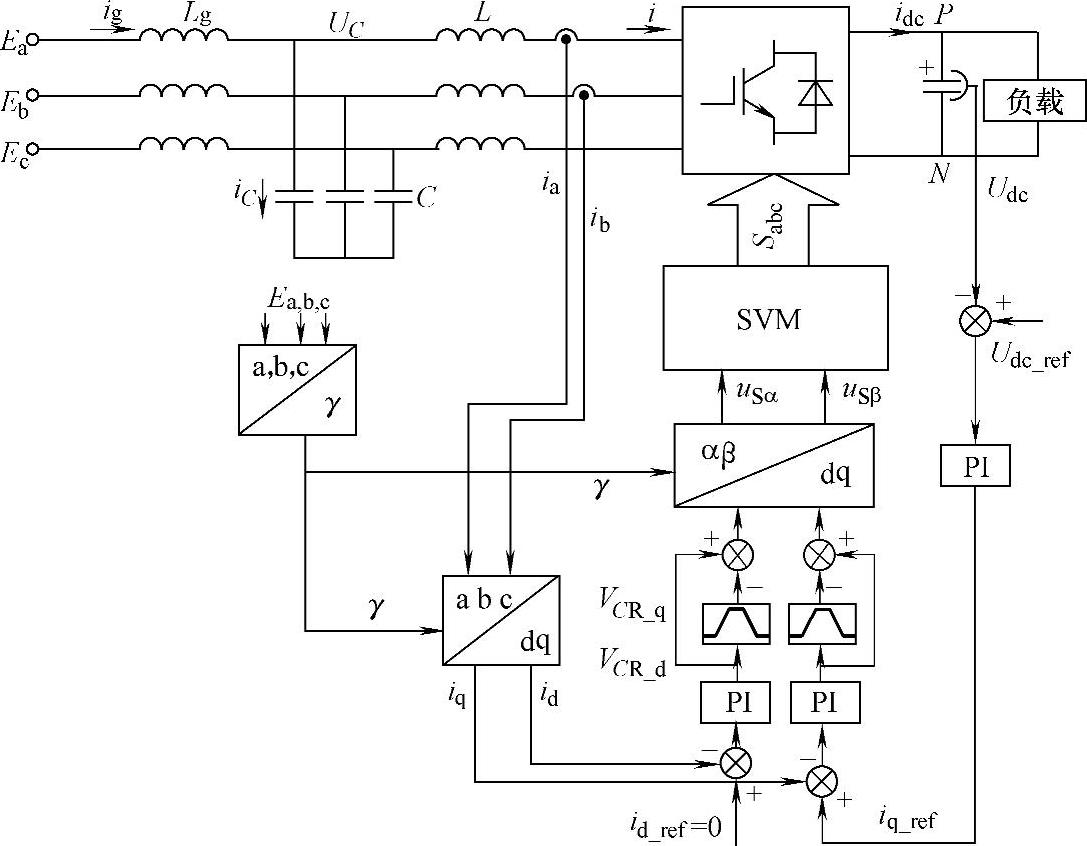
图5-51 基于双带通滤波器的有源阻尼控制结构图

从图5-51看出，基于双带通滤波器的有源阻尼控制的基本思想是将电流内环PI调节器输出值经过一个带通滤波器后，再与PI调节器的输出值相减，从而获得陷波器特性，实现了LCL并网逆变器的有源阻尼控制。