基于电压定向的直接功率控制（V-DPC）优化方案

5.3.2.1 并网逆变器DPC中瞬时功率的计算

1.有电网电压传感器时的瞬时功率的计算

在并网逆变器的DPC中，需要计算网侧的瞬时功率，因此只需要将上述瞬时功率计算中的电压矢量U以电网电压矢量E代之即可。一般情况下，并网逆变器的控制均采用电网电压传感器以检测电网电压，例如当采用基于两相静止αβ坐标系的瞬时功率计算时，仅需将检测得到的三相电压e_a、e_b、e_c和电流i_a、i_b、i_c通过T_abc/αβ变换得到e_α、e_β和i_α、i_β，再由式（5-30）和式（5-32）即可计算得到相应的瞬时有功功率和无功功率。

2.无电网电压传感器时的瞬时功率计算

在并网逆变器的控制中，一般情况下共用到了三种传感器：①交流电流传感器；②直流电压传感器；③电网电压传感器。实际应用中，由于系统控制和系统保护（输出侧过电流保护和直流母线过电压保护）的需求，交流电流传感器、直流电压传感器必不可少。而针对电网电压传感器，为降低成本和提高系统的可靠性，有时则可能被省略，为此必须通过算法可以对电网电压值进行估计。以下介绍无电网电压传感器时的瞬时功率计算和电网电压估算方法。

首先由式（5-27）可得并网逆变器的瞬时复功率表达式为

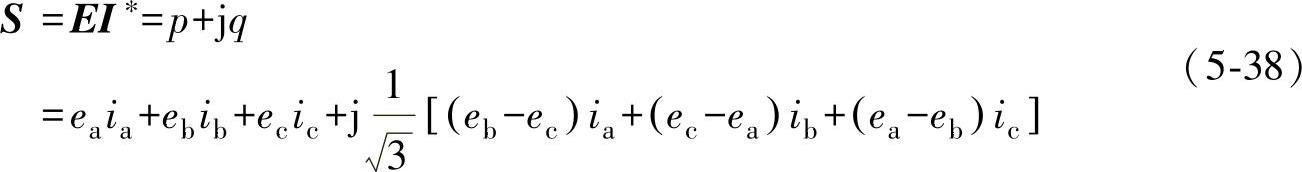
其中，并网输出电流的瞬时值i_a、i_b、i_c是直接由传感器检测得到的，但由于没有电网电压传感器，因此电网电压的瞬时值e_a、e_b、e_c为未知量。实际上，电网电压可以通过基于瞬时功率的电网电压估算方法进行估算，其主要思想是：将并网逆变器瞬时功率表达式中的电网电压用所检测的逆变器输出电流和直流侧电压进行描述，进而通过逆变器回路的电压方程运算获得电网电压的估算值。采用这种方法先运算出瞬时有功、无功功率的估算值，再得出电网电压的估算值，而瞬时有功、无功功率的估算值可作为直接功率控制器的反馈信号。具体讨论如下：

由式（5-38），并网逆变器输出的瞬时无功功率q为

式中 e_bc=e_b-e_c。

设并网逆变器开关调制时a、b、c各相的开关函数分别为S_a、S_b、S_c。这里，当上桥开关管导通时，令S_x（x=a、b、c）=1，而当下桥开关管导通时，令S_x（x=a、b、c）=0。如果忽略并网逆变器输出回路中电阻的影响，则可得并网逆变器中的电网电压表达式为

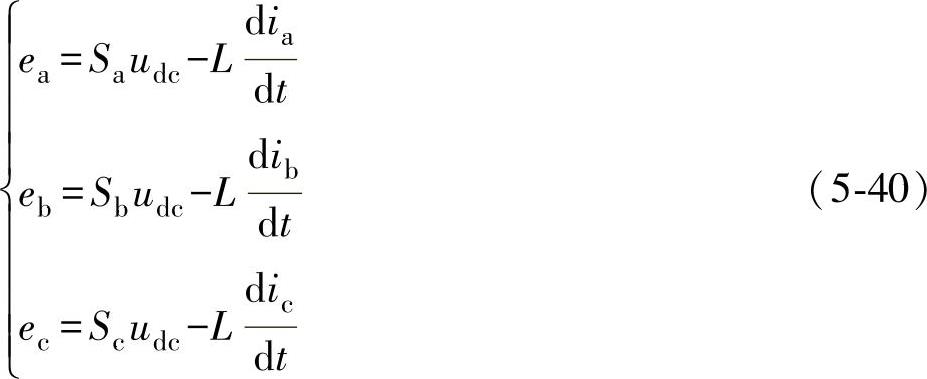
对应的线电压形式为

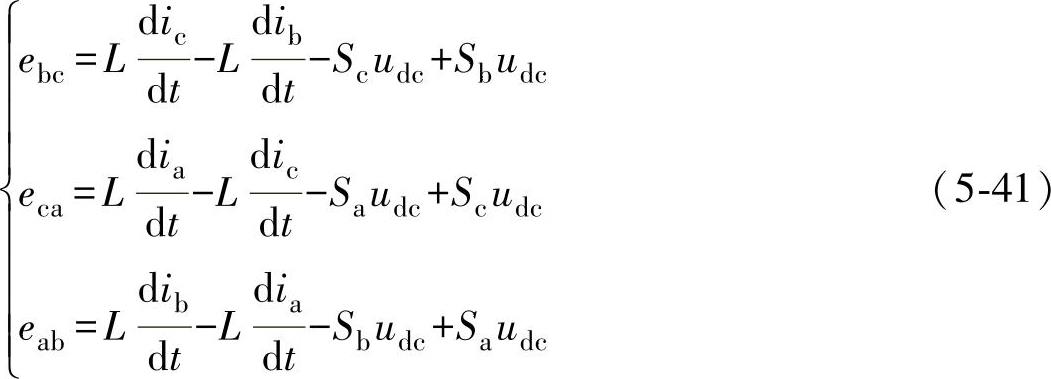
联立式（5-40）和式（5-38），可得瞬时有功和无功功率的估算值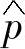、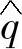分别为

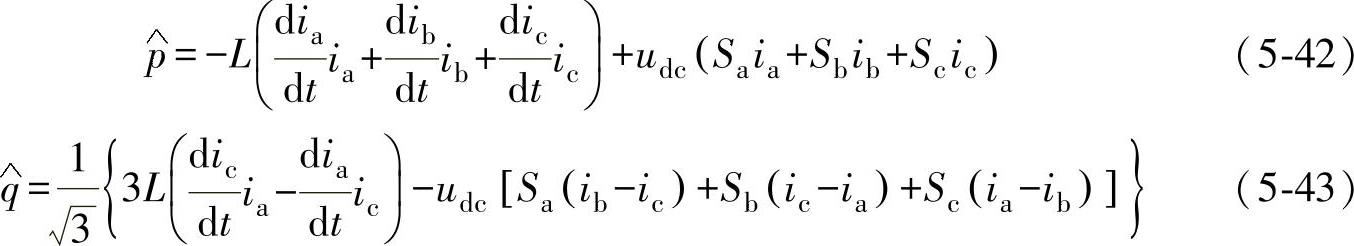
由式（5-42）和式（5-43）可以看出：瞬时有功和无功功率的估算值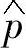、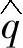不仅与逆变器的开关状态有关，而且与滤波电感参数有关。可见并网逆变器瞬时有功和无功功率估算的精度取决于电感参数的准确程度。

从式（5-42）、式（5-43）可看出，功率估算中存在电流微分的运算，然而实际计算时微分由差分运算来代替。为了使电流的差分运算尽可能准确，应当尽量避免电流尖峰的影响。为此，一方面要求交流侧采用尽量大的电感进行滤波；另一方面，由于估计值与开关状态有关，因而采样及估算时应当避开开关动作的时刻，以减小误差。

获得瞬时有功和无功功率的估算值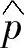、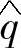后，再由并根据关系式S=EI^∗得

SI=EI^∗I=EI² （5-44）

从而估算的电网电压矢量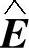为

将式（5-45）写成基于αβ坐标系的矩阵形式，即

可见，通过检测并网逆变器的输出电流i_a、i_b、i_c，并经过坐标变换运算，即得αβ坐标系下的输出电流（i_α，i_β），将i_α、i_β以及由式（5-42）、式（5-43）得到的瞬时有功、无功功率的估算值、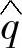代入式（5-46），即可得基于αβ坐标系的电网电压的估算值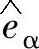、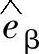，从而可由式（5-2）求得电网电压矢量的位置角估算值。

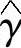5.3.2.2 无电网电压传感器的V-DPC结构

基于电网电压定向的直接功率控制（V-DPC）是DPC基本的控制策略，一般可采用有电网电压传感器的V-DPC。但也可以利用上述电网电压的估算来实现无电网电压传感器的V-DPC，其控制系统结构如图5-18所示（图中略去了输出滤波器等效电阻的影响），其基本的控制思路为：

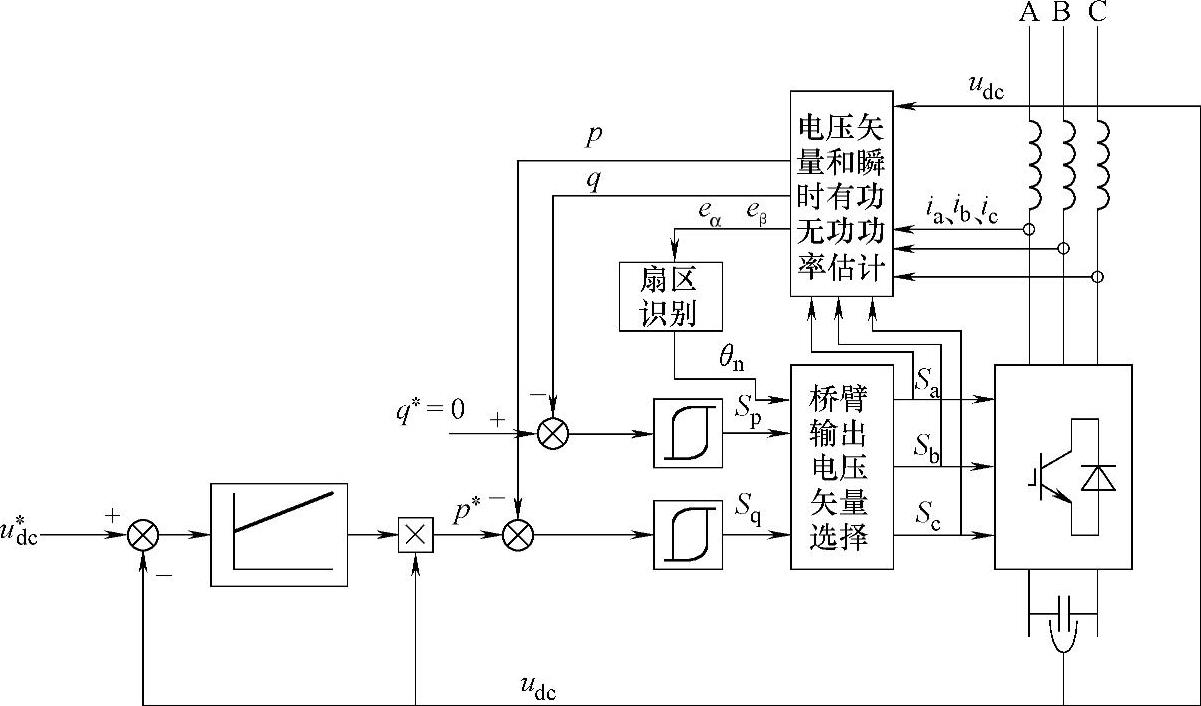
图5-18 无电网电压传感器的V-DPC结构

功率和电压估算单元根据并网逆变器的开关函数（S_a、S_b、S_c）、输出电流检测值（i_a、i_b），以及直流侧电压检测值u_dc经过式（5-42）、式（5-43）以及式（5-46）计算，得到瞬时有功、无功功率的估计值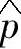、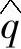以及三相电网电压在αβ坐标系下的估计值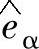、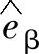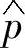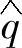；、与瞬时有功、无功参考值p^∗和q^∗比较后送入滞环比较器，得到相应的S_p、S_q信号；瞬时有功功率参考值p∗由直流电压外环调节器输出给定，而瞬时无功功率参考值q^∗则由系统的无功指令给定，若使并网逆变器单位功率因数运行，则q^∗=0；由式（5-2）及e_α、e_β可算出电网电压矢量的位置角估算值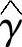，从而可判断出电网电压矢量所处扇区的信息θ_n；最后根据S_p、S_q和θn通过既定开关表的查表获得所需输出电压的开关函数S_a、S_b、S_c，以驱动逆变器的开关管调制，同时将此开关状态信号反馈给功率和电压估算单元，以便功率和电压的估计。

关于并网逆变器输出瞬时有功、无功功率的估计，以上已经作了介绍。而在图5-18所示的V-DPC结构中，其控制的关键在于：将瞬时功率的参考值与瞬时功率的估算值比较后，其差值输入到功率滞环比较器中，并根据功率滞环比较器的输出和电压矢量位置查相应的开关表，以获得开关状态输出。另外，对于DPC而言，功率管开关频率的限定控制也较为关键。以下将研究功率滞环比较器、开关表以及开关频率的限定控制等。

5.3.2.3 功率滞环比较器

功率滞环比较器是DPC控制器的关键环节，主要包括有功功率滞环比较器和无功功率滞环比较器。在无电网电压传感器的V-DPC系统中，功率滞环比较器的输入分别为：瞬时有功功率参考值与瞬时有功功率估算值的差值Δp，以及瞬时无功功率参考值与瞬时无功功率估算值的差值Δq。功率滞环比较器的输出是反映实际功率偏离给定功率程度的开关状态量S_p和S_q。功率滞环比较器的滞环特性如图5-19所示。

图5-19 滞环比较器滞环特性

a）有功功率滞环比较器滞环特性 b）无功功率滞环比较器滞环特性

图5-19中：S_p和S_q只有1或0两种状态。

针对图5-19a所示的有功功率滞环比较器特性，其输入输出判据为

当Δp＞H_p时，S_p=1；当-H_p＜Δp＜H_p时，dΔp/dt＜0，S_P=1；

当Δp＜-H_p时，S_p=0；当-H_p＜Δp＜H_p时，dΔp/dt＞0，S_p=0。

其中，Δp=p^∗-p，2H_p为有功功率滞环比较器滞环宽度。

同理，针对图5-19b所示的无功功率滞环比较器特性，其输入输出判据为：

当Δq＞H_q时，S_q=1；当-H_q＜Δq＜H_q时，dΔq/dt＜0，S_q=1；

当Δq＜-H_q时，S_q=0；当-H_q＜Δq＜H_q时，dΔq/dt＞0，S_q=0。

其中，Δq=q^∗-q，2H_q为无功功率滞环比较器滞环宽度。

综上可得

可见，当瞬时功率偏差量的绝对值大于滞环宽度时，开关状态改变以使其偏差量减小，而在偏差量绝对值减小的过程中，则保持开关状态不变，直到其偏差量绝对值反向增大且再次超过滞环宽度时，开关状态才再次改变。

应当注意的是：滞环宽度H_p、H_q的大小将直接影响并网逆变器输出电流的THD、平均开关频率和瞬时功率跟踪能力。例如，当滞环宽度增加时，并网逆变器的开关频率随即降低，而谐波电流则相应增大，功率跟踪能力也随之下降。

5.3.2.4 开关状态表

如图5-20所示，三相电压型逆变器的电压空间矢量有8个矢量组成，即U₀、U₁、…、U₇，其中，U1～U6为非零矢量，U₀、U₇为零矢量，电压矢量其值又由S_a、S_b、S_c和u_dc决定，即S_aS_bS_c=000∶111对应于U₀∶U₇[U₀（000）、U₁（100）、U₂（110）、U₃（010）、U₄（011）、U₅（001）、U₆（101）、U₇（111）]。由于开关状态的获得不仅和滞环比较器的输出结果有关，还和电网电压矢量所在的矢量区域位置有关，这种区域位置通常采用矢量“扇区”表示。以下首先介绍矢量“扇区”的划分方法，接着介绍相关开关状态表的形成。

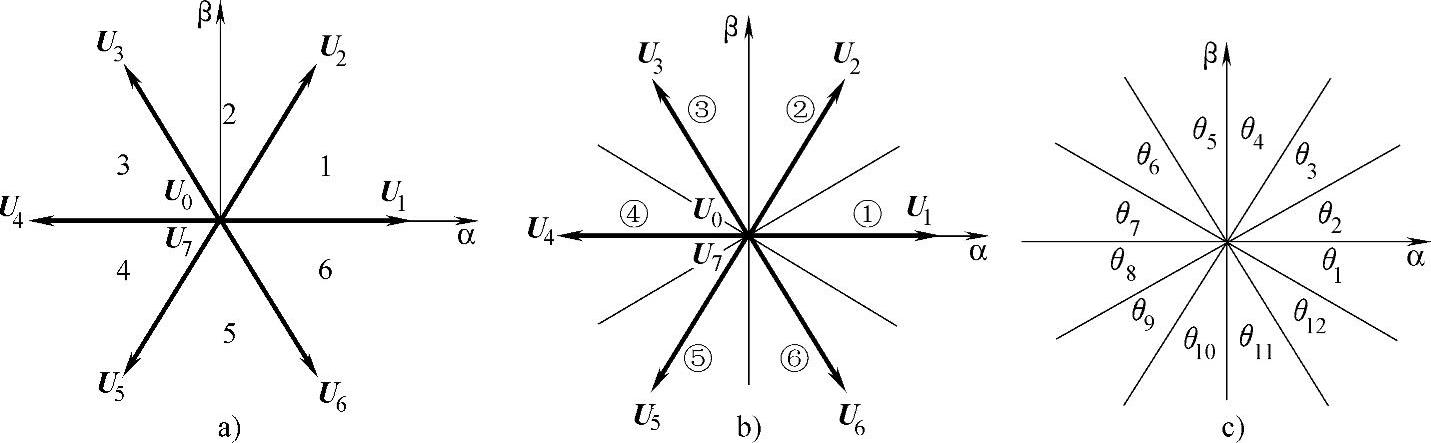
图5-20 矢量“扇区”的划分方法

a）依据电压空间矢量划分的1～6矢量“扇区” b）以电压空间矢量为中线划分的①～⑥矢量“扇区” c）结合a）和b）矢量“扇区”形成的θ₁～θ₁₂矢量“扇区”(www.xing528.com)

1.矢量“扇区”的划分

第一种矢量“扇区”的划分方法：该方法是通过电压型逆变器输出的6个非零电压空间矢量将αβ平面分成6个独立的矢量“扇区”，如图5-20a所示的1～6“扇区”。这种划分方法形成了一个正六边形，分别由6个非零电压空间矢量（U_k，k=1，2，…，6）和两个零电压矢量（U₀，U₇）组成。这种扇区划分方法在空间矢量的调制中得到了广泛的应用，并可以通过参考电压矢量所在“扇区”的两个相邻的非零电压矢量和一个零电压矢量的合成来实现参考电压矢量的跟踪控制。然而，在直接功率控制中，瞬时功率的滞环比较代替了参考电压矢量的跟踪控制，因而空间矢量调制方法不能直接用于调节瞬时功率。

实际上，通过改变开关函数，这种“扇区”的划分仍然可以用于瞬时功率的跟踪控制，而通过控制并网逆变器输出电压的幅值和相位就可以达到调节逆变器输出功率的目的。

第二种矢量“扇区”划分的方法：该方法以电压型逆变器的6个非零电压空间矢量作为中线，将αβ平面分成滞后第一种矢量“扇区”30°的6个矢量“扇区”，如图5-20b所示的①～⑥矢量“扇区”。当然，这种矢量“扇区”的划分同样可以实现瞬时功率的跟踪控制。

第三种矢量“扇区”划分的方法：该方法是将上述两种划分的矢量“扇区”重叠，从而将αβ平面划分成12个矢量“扇区”，如图5-20c所示的θ₁～θ₁₂矢量“扇区”，12个矢量“扇区”在αβ平面的相角范围计算式为。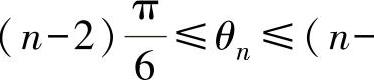

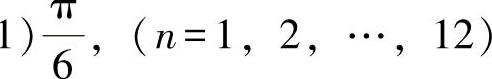为确定电网电压矢量所处区间，由e_α、e_β确定矢量E的相角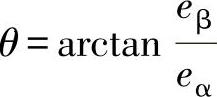，再根据上述相角范围计算式确定矢量E所处区间。例如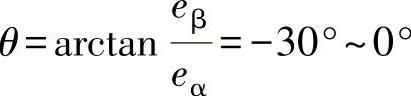，说明电压空间矢量E在θ₁扇区内。

2.开关状态表的确定

由于并网逆变器中每个电压矢量U₀∶U₇对瞬时有功功率和无功功率的影响是不同的，因此必须通过选择合适的电压矢量实现对输出瞬时有功、无功功率的调节。而开关表状态表就是通过滞环比较器的输出结果以及电网电压矢量的位置来确定DPC控制所需的开关状态S_a、S_b、S_c。而S_a、S_b、S_c的取值即决定了所需的逆变器桥臂输出电压矢量U_r。

由并网逆变器的主回路分析，若略去输出电感等效电阻的影响，可得

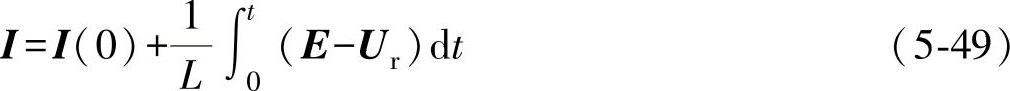
其中，U_r为逆变器桥臂输出电压矢量。

如果考虑一个采样周期T的时间间隔，且在采样周期T中E-U_r不变，并假设当前0时刻的电流矢量为I，而此时的参考电流矢量为I^∗，则此时式（5-49）可以改写为

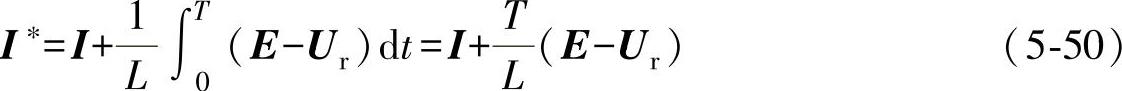
式（5-50）表明，在一个采样周期T中，为了使电流矢量I能跟踪参考电流矢量I^∗，则必须使逆变器输出合适的电压矢量U_r，使电流矢量I沿E-U_r矢量方向跟踪参考电流矢量I^∗。

如图5-21a所示，设E在θ₁区域，I^∗为与p^∗、q^∗相对应的电流矢量，若I滞后并小于I^∗，此时p^∗-p＞H_p，q^∗-q＞H_q，由式（5-47）、式（5-48）得：S_p=1、S_q=1。这种情况下，应选择逆变器输出的空间电压矢量U₅（001），从而使电流矢量I沿E-U₅矢量方向趋近于I^∗，从而使p趋近于p^∗，q趋近于q^∗，从而确定S_aS_bS_c=001。

为了进一步研究开关表的基本规律，以下分成两种情况加以研究：

1）设矢量E分别在θ₂、θ₃两区域，且p＞p^∗+H_p，即S_p=0，如图5-21b所示。此时，若q＜q^∗-H_q，即S_q=1，则无论E在θ₂区或θ₃区，均应选取U₁（100），以使电流矢量I沿E-U₁矢量方向趋近于I^∗，此时S_aS_bS_c=100；若q＞q^∗+H_q，即S_q=0，则无论E在θ₂区或θ₃区，均应选取U₂（110），以使电流矢量I沿E-U₂矢量方向趋近于I^∗，此时S_aS_bS_c=110。变换区域分析不难发现：当S_p=0时，所选择的U_r矢量一定是包围E矢量的1～6矢量“扇区”边界的矢量之一，最终再由S_q的状态值加以选定。

2）设矢量E分别在θ₁、θ₂两区域，且p＜p^∗-H_p，即S_p=1，如图5-21c所示。此时，若q＜q^∗-H_q，即S_q=1，则无论E在θ₁区或θ₂区，均应选取U₅（001），以使电流矢量I沿E-U₅矢量方向趋近于I^∗，此时S_aS_bS_c=001；若q＞q^∗+H_q，即S_q=0，则无论E在θ₁区或θ₂区，均应选取U₃（010），以使电流矢量I沿E-U₃矢量方向趋近于I^∗，此时S_aS_bS_c=010。变换区域分析不难发现：当S_p=1时，所选择的U_r矢量定是与E矢量成钝角且与包围E矢量的①～⑥矢量“扇区”边界相垂直的空间电压矢量之一，最终再由S_q的状态值加以选定。

图5-21 不同S_p、S_q状态值时的U_r矢量的选取规律示意

a）电流矢量跟踪和逆变器空间电压矢量U_r的选择 b）当S_p=0且S_q不同取值时，U_r矢量的选取规律示意 c）当S_p=1且S_q不同取值时，U_r矢量的选取规律示意

同样可对E处于其他扇区及对应的滞环比较输出结果S_p、S_q进行分析，于是得到开关表见表5-1。

表5-1 开关表

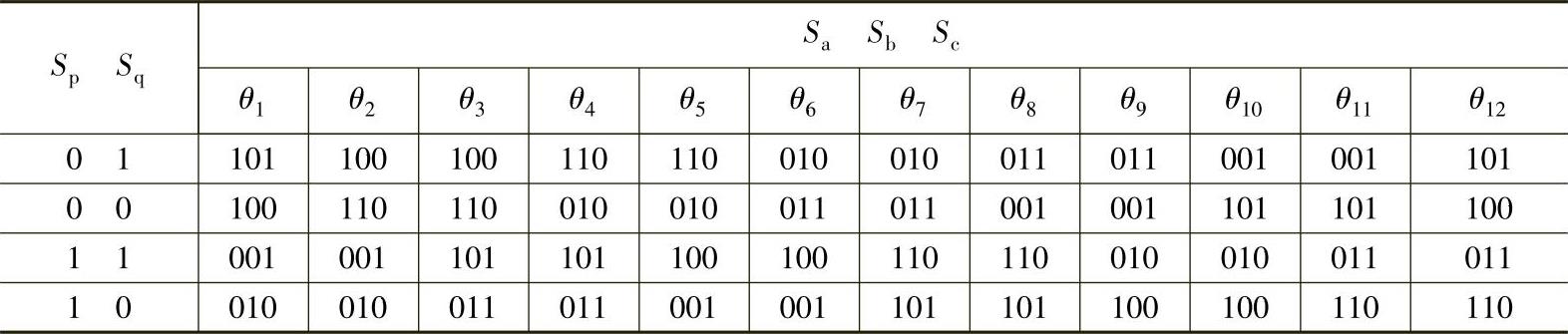
从上表可以看出，没有使用两个零矢量（U₀，U₇），并且当Δp≤H_p和Δq＜H_q时，原U_k（k=0，…，7）不切换，从而在限制平均开关频率的同时，增加了控制的稳定性。

由于有功功率和无功功率是根据θ_n和S_p、S_q通过查开关表5-1选择S_a、S_b、S_c，即选择U_r实时调节的。选择的U_r具有同时调节有功功率和无功功率的能力，即大了往小调，小了往大调。因此，开关表是并网逆变器DPC控制的核心。

5.3.2.5 开关频率控制

由于滞环控制中开关频率的不确定性，因此应采取一定措施将其开关频率限定在一定范围内。为此首先应当从并网逆变器的数学模型出发寻找影响开关频率大小的因素。

并网逆变器dq坐标系中的电压方程为

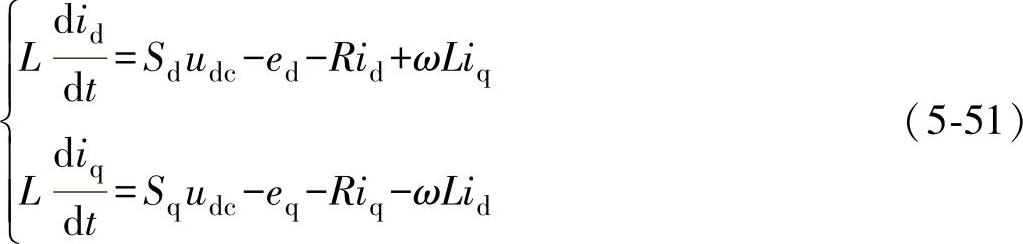
式中 S_d、S_q——开关函数在d、q轴上的分量。

当采用电网电压定向时，因为采用的是“等功率”坐标变换，因而有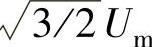：，e_q=0（U_m为电网相电压幅值）。代入同步坐标系下瞬时功率表达式（5-36）和式（5-37）得

将等式（5-51）两边同乘以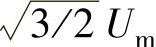，可得并网逆变器的功、无功功率p、q为变量的功率方程：

其中，，。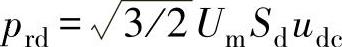

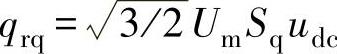若忽略输出滤波器的等效电阻R，当逆变器运行于单位功率因数时，q=0时，则式（5-53）可化简为

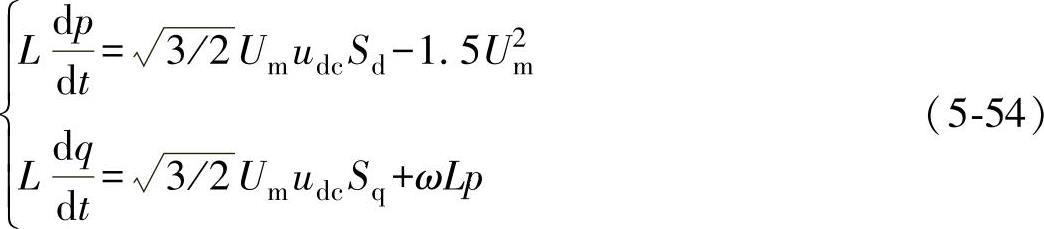
考虑到“等功率”变换中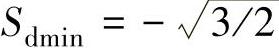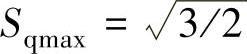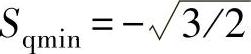，、、、，因而由式（5-54）可得

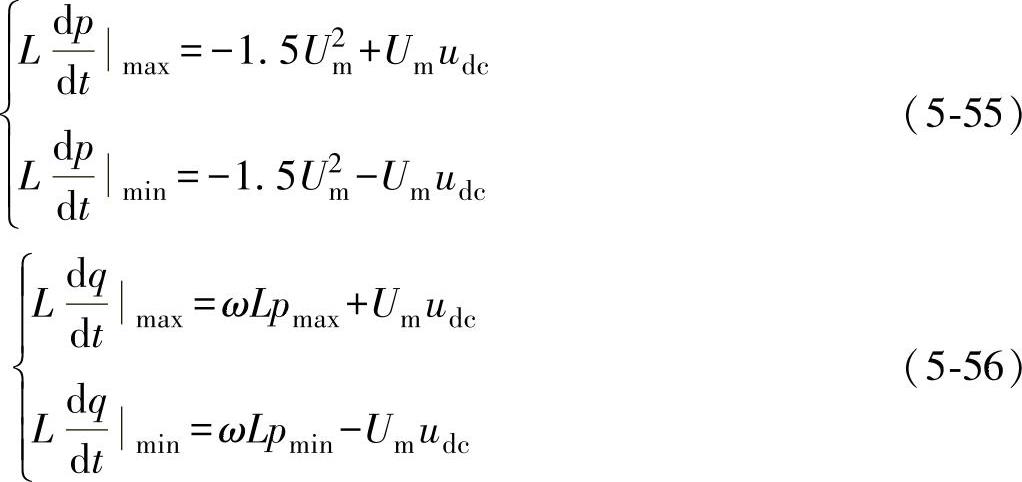
若令T为开关频率f_s所对应的开关周期，则|dp/dt|=2H_p/T=2H_pf_s，由式（5-55）可得

2LH_p（f_smaxp+f_sminp）=3U²m （5-57）

其中，f_smaxp、f_sminp分别对应有功功率模值变化率最大和最小时的最大开关频率和最小开关频率。从而可得有功功率滞环控制的平均开关频率f_savp表达式为

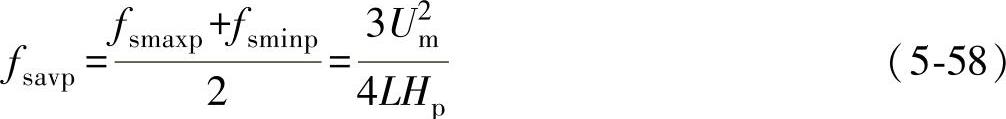
同理，根据式（5-56）及dq/dt=2H_q/T=2H_qf_s可得无功功率滞环控制的平均开关频率f_savp的表达式为

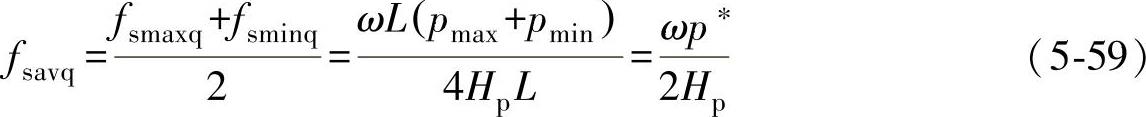
其中，f_smaxq、f_sminq、f_savq分别为对应于无功功率p在2H_p变化范围内的最高、最低和平均开关频率，p_∗为有功功率参考值。

由于利用并网逆变器的输出电压空间矢量同时对相互独立的p和q进行调节，则开关频率平均值f_sav应取f_savp和f_savq的几何平均值，即

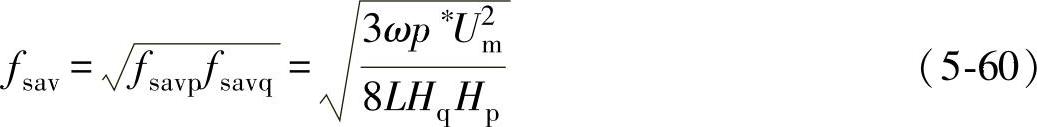
由式（5-60）可以看出：当U_m、p^∗一定时，平均开关频率f_sav的平方与电感L、H_qH_p成反比，因而H_qH_p和L不能太小，以免f_sav过高。当U_m、p^∗及L一定时，f_sav增大，则H_qH_p变小，即动态跟踪偏差减小，而当f_sav→∞时，H_qH_p→0，则无动态跟踪偏差。

事实上，由于功率开关管受其能量等级的限制，需要将开关频率限制在一定的范围之内。一种有效的方法就是使用可变滞环宽度的滞环比较器，并将开关管的平均开关频率限制在开关器件所允许的范围内。对于某一确定系统，可以采用调节滞环宽度的方法限制开关管的平均开关频率，即：当滞环宽度增加时，平均开关频率将减小；而当滞环宽度减小时，则平均开关频率将增大。显然，滞环控制精度与开关频率间存在矛盾，为此，可采用以下平均开关频率的调节方法，即

1）在暂态时使用大的滞环宽度以限制开关频率，当系统进入稳态时，使滞环宽度变小从而减小输出电流谐波。

2）通过计算半个周期内开关脉冲上升沿的数目来计算平均开关频率。如果平均开关频率过高，则使滞环宽度增加；如果平均开关频率减小，则适当增减小滞环宽度。