瞬时功率的计算方法

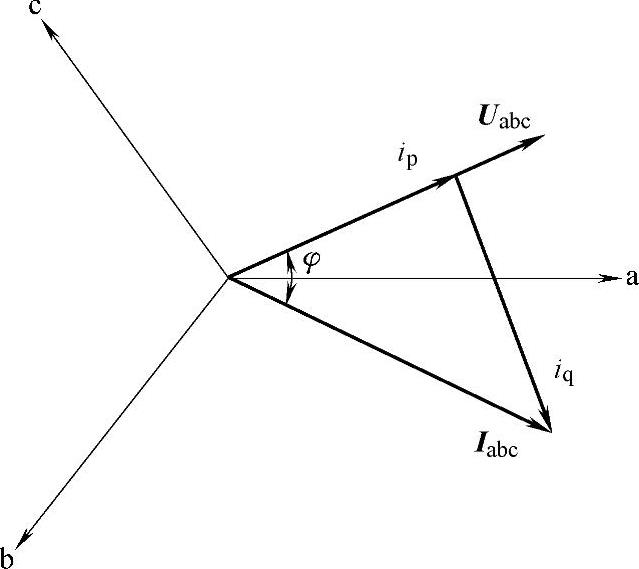
图5-17 电流矢量I_abc的有功、无功电流分量i_p和iq

由于DPC是基于并网逆变器输出瞬时有功、无功功率的闭环控制，因而一般基于平均值定义的有功功率和无功功率定义方法将不再适用，本节介绍了瞬时功率和瞬时功率因数的定义，并讨论了不同坐标系中的瞬时功率计算方法。

5.3.1.1 瞬时功率的定义

在三相交流电路中，三相静止abc坐标系中的相电压矢量U_abc和相电流矢量I_abc如图5-17所示，并可由相应的瞬时值表示为U_abc=[u_au_bu_c]和I_abc=[i_ai_bi_c]。

在图5-17中，若以电压矢量U_abc定向，则电流矢量I_abc可分解为相应的有功电流分量i_p（与电压矢量U_abc同向）和无功电流分量i_q（与电压矢量U_abc垂直），其中电压矢量U_abc和电流矢量I_abc的模分别为。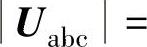

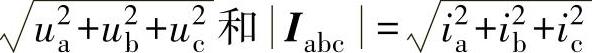如图5-17中的矢量定向，瞬时有功功率p定义为相电压矢量U_abc与相电流矢量I_abc的标量积，而瞬时无功功率q则定义为相电压矢量U_abc与相电流矢量I_abc矢量积的模，即

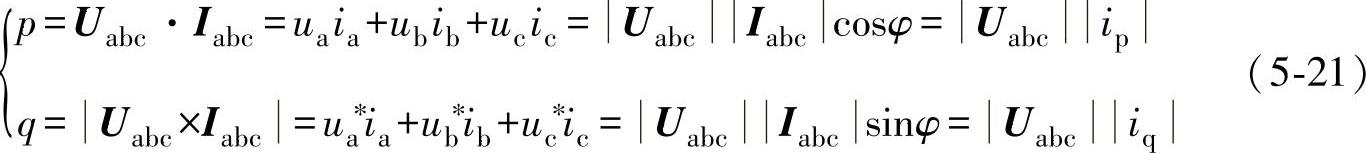
针对图5-17中的瞬时功率定义，参照三相正弦交流电路中功率因数的定义，相应的瞬时功率因数也可以定义为λ=cosφ，其中φ为图5-17所示的电压矢量U_abc与电流矢量I_abc的相位差，显然

5.3.1.2 三相静止abc坐标系下瞬时功率的计算

根据式（5-21）、式（5-22），三相静止坐标系下的瞬时有功功率p和瞬时无功功率q也可写成

式中，u_a^∗、u_b^∗、u_c^∗满足

另外，由于相电压矢量U_abc与相电流矢量I_abc的矢量积仍然为矢量，显然瞬时无功功率也可由三相静止坐标系下的无功矢量Q_abc表示为

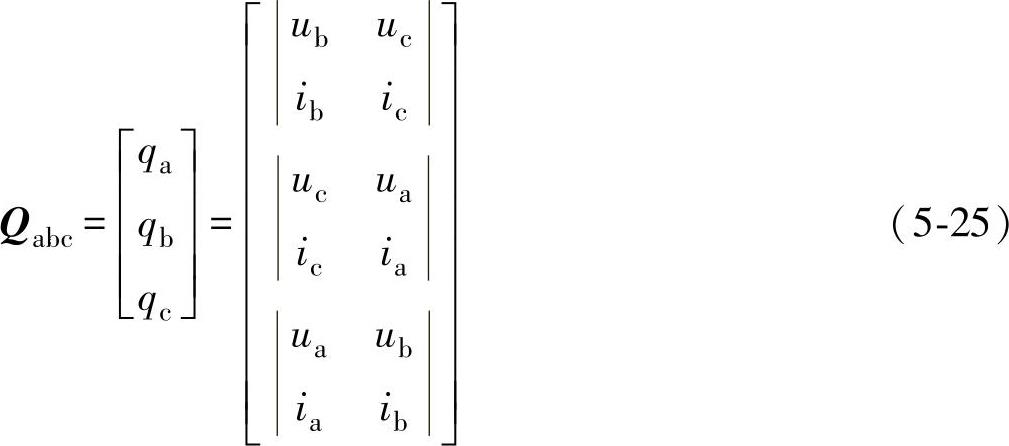
由此，可得瞬时无功功率q为

实际上，瞬时有功功率和瞬时无功功率可由定义在复平面上的复功率S获得，而复功率S为电压矢量U_abc和电流共扼矢量I_a^∗_bc的标量积，即

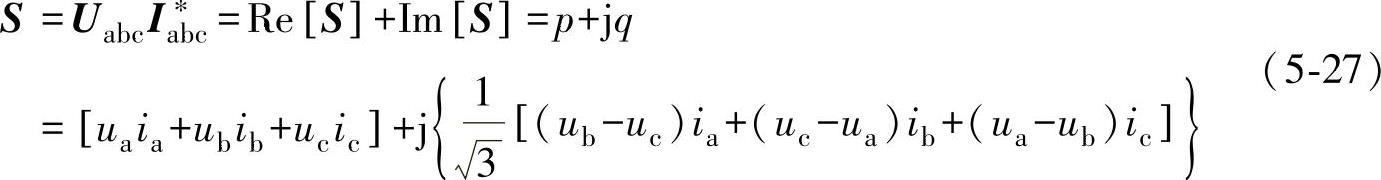
可见，从复平面角度看，瞬时有功功率p实际上是瞬时复功率S在实轴上的投影，而瞬时无功功率q则是瞬时复功率S在虚轴上的投影。换言之，瞬时复功率S的实轴分量即为有功分量，而瞬时复功率S的虚轴分量即无功分量，显然有功分量比无功分量超前90°。

5.3.1.3 两相静止αβ坐标系下瞬时功率的计算

设三相静止abc坐标系到两相静止αβ坐标系的“等功率”变换矩阵为T_abc/αβ，则(www.xing528.com)

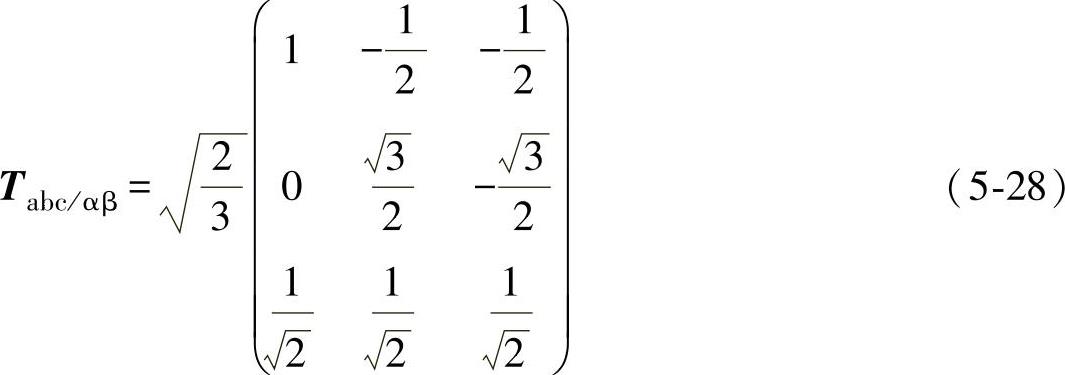
将三相坐标系中的矢量U_abc、I_abc经T_abc/αβ变换后，得在αβ坐标系中电压、电流矢量U_αβ、I_αβ的表达式为

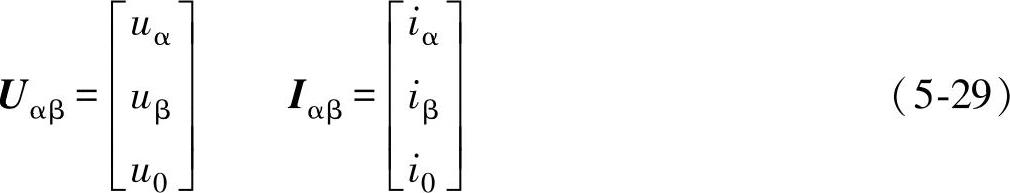
式中 i₀、u₀——零序电流、电压分量。

若为三相三线制连接，即没有零序电流分量，即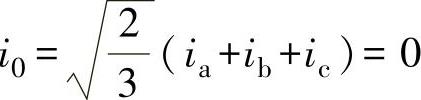；又由于在三相三线制中，相电压的零序分量不起作用，可令u₀=0。

这样，基于αβ坐标系的瞬时有功功率p的计算式为

p=U_αβ·I_αβ=u_αi_α+u_βi_β （5-30）

同理，瞬时无功功率也可由两相静止αβ坐标系下的无功矢量Q_αβ表示为

Q_αβ=U_αβ×I_αβ=（u_αi_β-u_βi_α）K （5-31）

式中 K——垂直于αβ坐标系的单位矢量。

显然，Q_αβ的模值∣Q_αβ∣即为瞬时无功功率q，观察式（5-30）不难得出基于αβ坐标系的瞬时无功功率q的计算式为

q=u_αi_β-u_βi_α （5-32）

则瞬时功率可用矩阵形式表示为

5.3.1.4 两相旋转dq坐标系下瞬时功率计算

设三相静止abc坐标系到两相同步旋转dq坐标系的变换矩阵为T_abc/dq，则

将三相abc静止坐标系中的矢量U_abc和I_abc变换到两相旋转dq坐标系后，得在dq坐标系下U_dq和I_dq表达式为

考虑到瞬时有功功率和瞬时无功功率的定义，则基于dq坐标系的瞬时有功功率p和瞬时无功功率q的计算式分别为

p=U_dq·I_dq=u_di_d+u_qi_q （5-36）

q=∣U_dq×I_dq∣=u_qi_d-u_di_q （5-37）