基于虚拟磁链定向的矢量控制（VFOC）优化方案

5.2.3.1 虚拟磁链的定向及VFOC

基于虚拟磁链定向的矢量控制（VFOC）是在基于电网电压定向的矢量控制（VOC）基础上发展出来的，是对VOC方案的一种改进。VOC方案的问题在于：当电网电压含有谐波等干扰时，就会直接影响电网电压基波矢量相角的检测，从而影响VOC方案的矢量定向的准确性及控制性能，甚至使控制系统振荡。为抑制电网电压对矢量定向及控制性能的影响，应当寻求能克服电网电压谐波影响的定向方法，即可考虑采用基于虚拟磁链定向的矢量控制（VFOC）。

虚拟磁链定向的基本出发点是将并网逆变器的交流侧（包括滤波环节和电网）等效成一个虚拟的交流电动机，如图5-10所示。其中，R_s、L可分别看作是该交流电动机的定子电阻和定子漏感，三相电网电压矢量E经过积分后所得的矢量Ψ=∫Edt便可认为是该虚拟交流电动机的气隙磁链Ψ。显然，由于积分的低通滤波特性，因此可以有效克服电网电压谐波对磁链Ψ的影响，从而确保了矢量定向的准确性。基于虚拟磁链定向的矢量控制（VFOC）的矢量图如图5-11所示，令磁链矢量Ψ与同步旋转坐标系的d轴重合，由于虚拟磁链矢量Ψ比电网电压矢量E滞后90°，因而当采用VFOC方案时，若控制并网逆变器运行于单位功率因数状态时，需满足：e_d=0、e_q=∣E∣，这样并网逆变器的输出瞬时功率即为

可见，通过控制与磁链矢量Ψ相重合的d轴电流分量i_d即可控制并网逆变器输出的无功功率，而控制与磁链矢量Ψ相垂直的q轴电流分量i_q即可控制并网逆变器输出的有功功率。显然，这与VOC方案中的d、q轴电流分量的有功、无功定义正好相反。

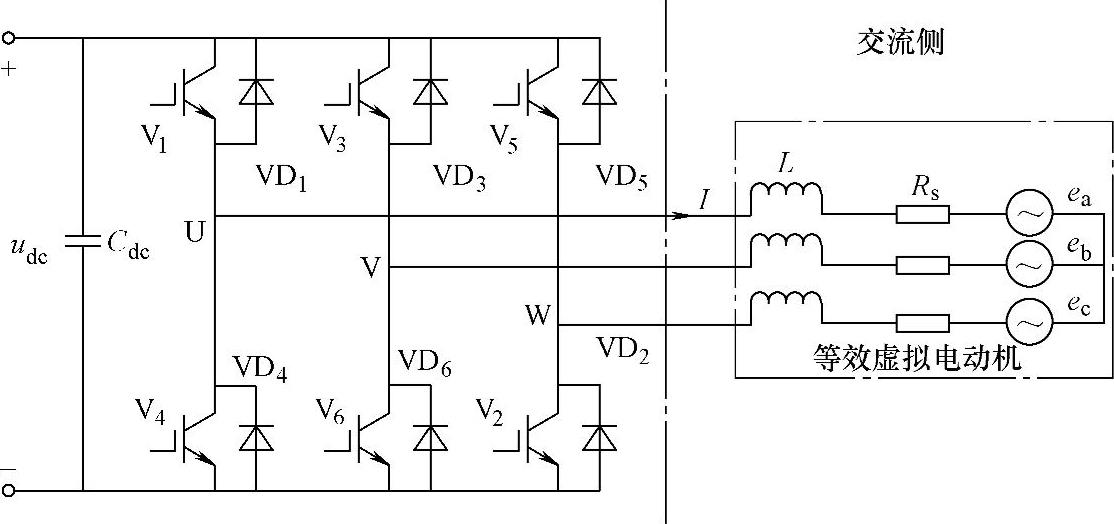
图5-10 交流侧等效虚拟电动机

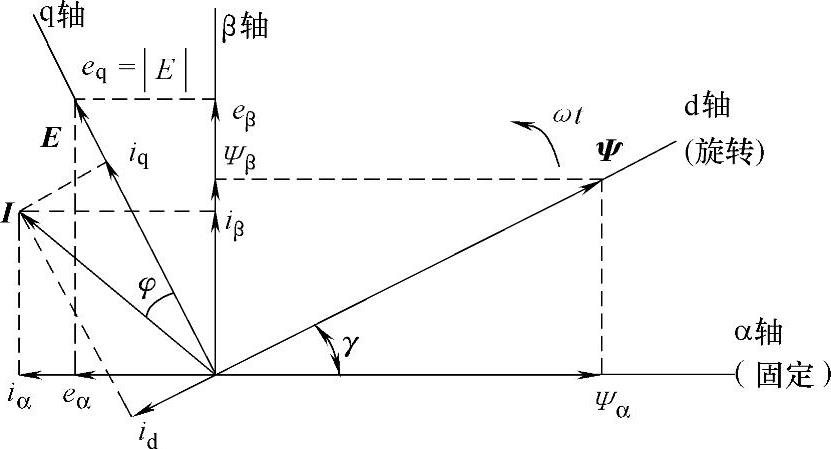
图5-11 基于虚拟磁链定向的矢量控制（VFOC）的矢量图

基于虚拟磁链定向的矢量控制（VFOC）的结构如图5-12所示，由于VFOC方案和VOC方案的被控对象没有改变，仅是定向矢量和dq轴变量性质有所不同，因而两者的控制结构是类似的。由于采用磁链矢量Ψ定向，Ψ的位置角γ由αβ坐标系下电网电压α、β轴分量e_α、e_β积分所得的磁链分量ψ_α和ψ_β计算而得，即

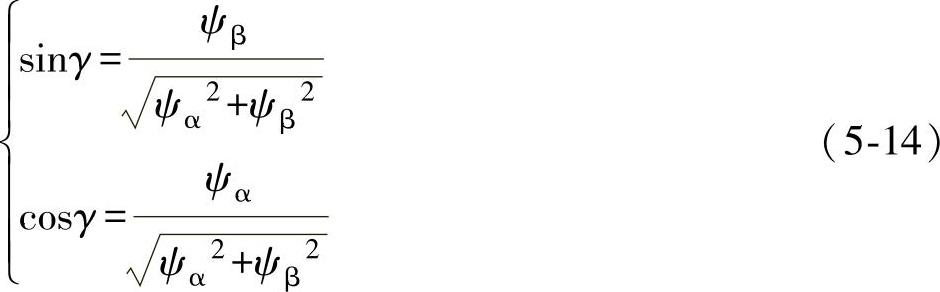
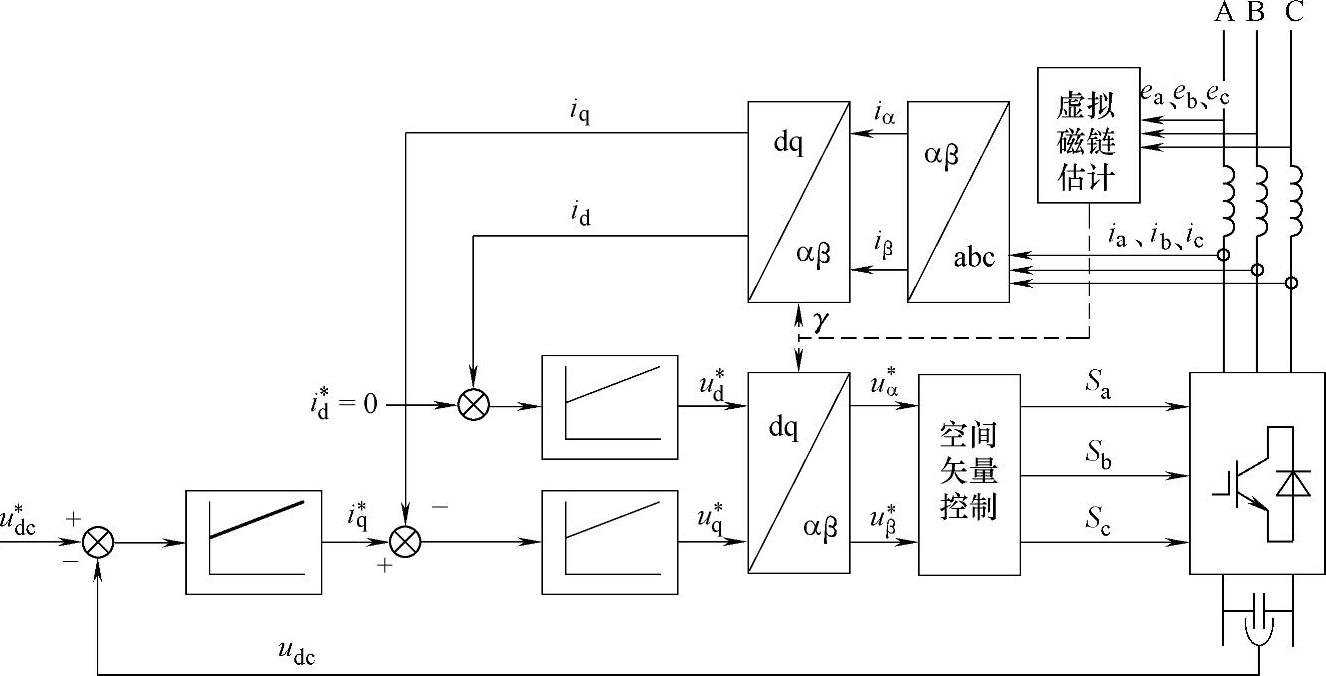
图5-12 基于虚拟磁链定向的矢量控制（VFOC）的结构

值得注意的是，基于虚拟磁链定向的矢量控制须克服积分漂移问题，否则将同样影响矢量定向的准确度，以下具体研究这一问题。

5.2.3.2 虚拟磁链定向时积分漂移的克服^[26，27]

当利用电网电压积分以进行虚拟磁链定向时，存在积分漂移问题，主要体现在以下两个方面：

1）当通过AD转换对电网电压进行采样时，由于采样电路中点电压的漂移，通常会导致采样结果中伴随着微小的直流分量，当这个直流分量控制在误差允许的范围内时，对系统实时控制的影响可以忽略。然而，为实现虚拟磁链的定向，则必须对电网电压进行积分，这样直流分量误差量会随着运行时间的增加而越来越大，最终严重影响系统的定向精度。

2）由于电网电压是一个正弦信号，而对正弦信号积分时，其积分结果中会出现一个和积分初值相关的直流分量，同样也会造成定向误差，即

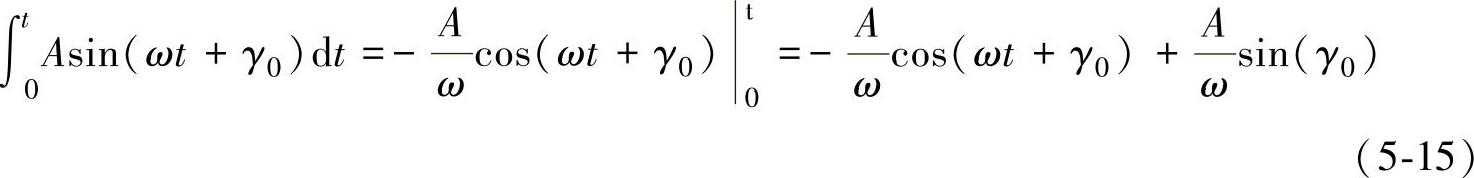
式中 Asin（ωt+γ₀）——电网电压信号，其中A表示其幅值，ω表示其角频率，γ₀表示积分开始时电网电压的初始相位角。

可见，只有当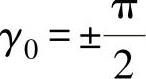时，积分结果中才不会出现这个直流分量。即使控制积分时刻，而从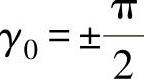这两个初始相位角开始进行积分，但由于实际电网频率的微小偏移也会造成积分起始时刻的偏移，从而同样无法消除这个直流分量误差，于是也可以导致虚拟磁链的定向误差。

为了能克服上述的两个问题，通常可采用低通滤波器（LPF）的W_LPF（s）=1/（s+ω_c）取代积分器，由于消除了积分运算，因而初始时刻引起的直流分量的积分效应被完全抑制，如图5-13所示。

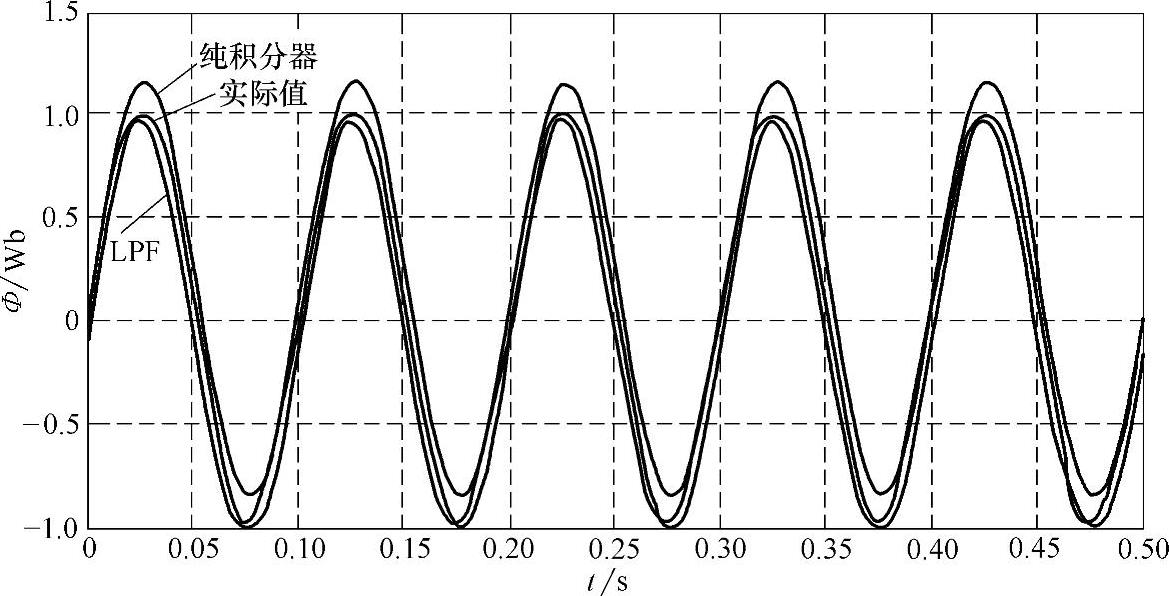
图5-13 纯积分与低通滤波器运算的对比(www.xing528.com)

假设输入为纯直流信号，经纯积分环节1/s和LPF环节1/（s+ω_c）的输出曲线分别如图5-14a、b所示。可见：若采用纯积分环节，微小的直流分量都将使积分器饱和，如图5-14a所示；而采用LPF环节替换之后，可以消除饱和现象，然而直流分量仍然存在，只能将直流分量降到原有的1/ω_c。

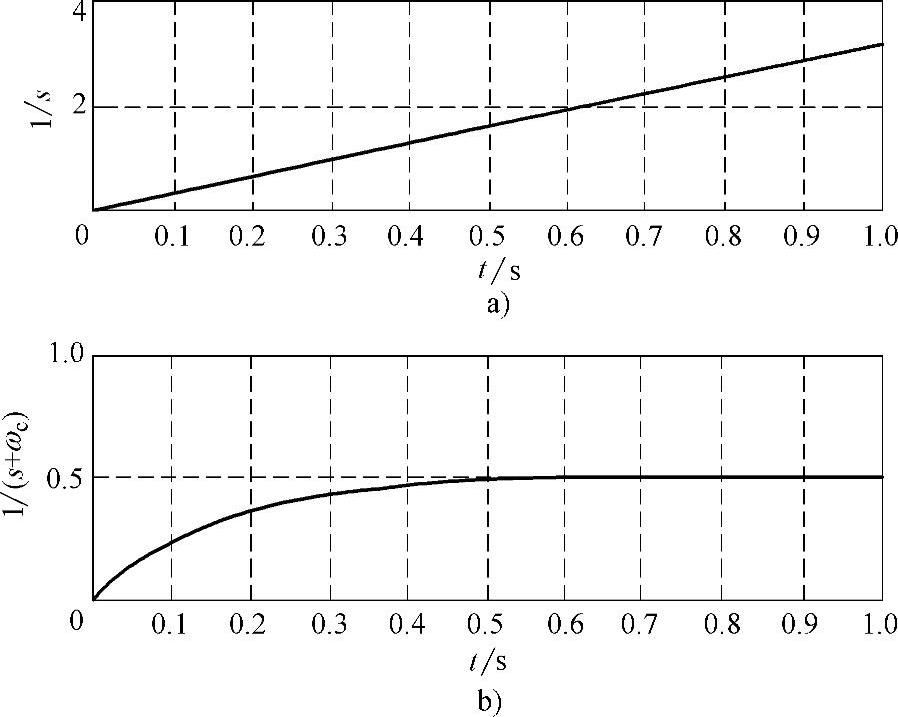
图5-14 两种算法对直流信号的响应

a）纯积分算法 b）低通滤波器算法

为了能彻底消除直流分量引起的误差，可采用改进的虚拟磁链观测模型^[26]，这不仅能解决初始相位问题，又能彻底消除直流分量带来的影响。这种改进的虚拟磁链观测模型的基本思路是将电网电压E经过低通滤波（LPF）之后再经过高通滤波（HPF）进行补偿，其传递函数为

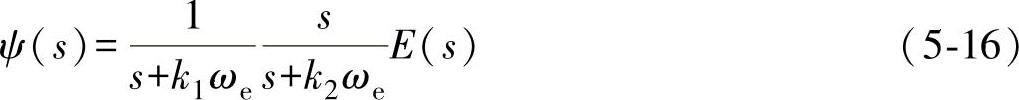
其中，LPF的截止频率为电网基波频率ω_e的k₁倍，HPF的截止频率为电网基波频率ω_e的k₂倍。k₁是正的常数，通常按照截止频率的最优范围可设定k₁为0.2～0.3，而k₂通常设定为k₁/2，这里取k₁=0.2，k₂=0.1。

将一个带有1%直流分量、初始相位为零的正弦信号输入串联的LPF和HPF，其输出结果和实际值的比较如图5-15所示。从图5-15可以看出，电网电压波形经过两个滤波器环节后的响应（如图中补偿前的波形）尽管很快消除了初值误差和直流分量的影响，但稳态时却与实际值之间存在相位和幅值偏差，为此需要对此结果予以补偿，具体的补偿算法讨论如下：

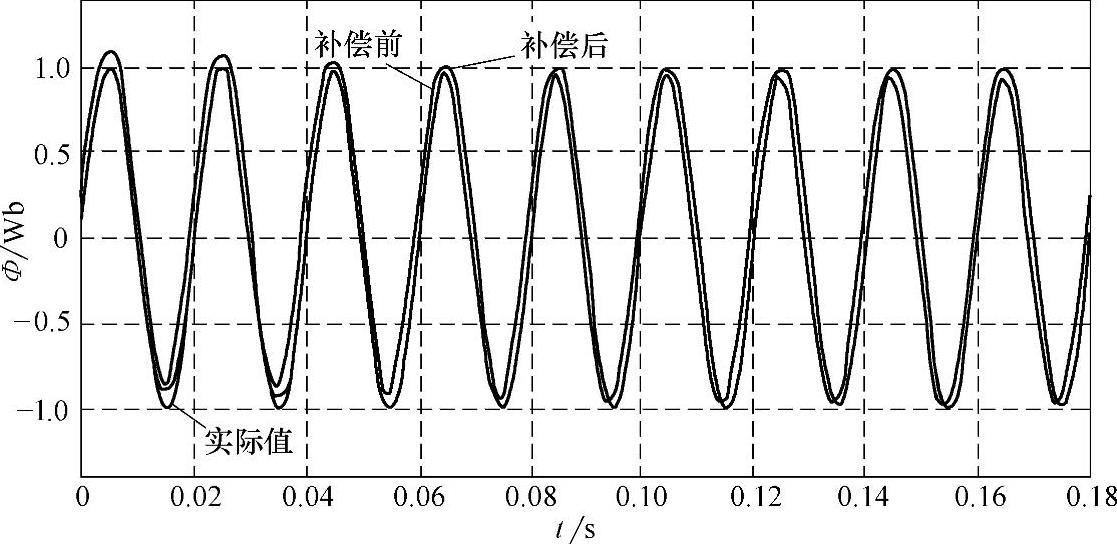
图5-15 改进算法对含有直流分量信号的响应

当采用理想积分器运算时，虚拟磁链矢量ψ和电网电压矢量E之间的关系是

而当采用式（5-16）所示的LPF和HPF运算时，有

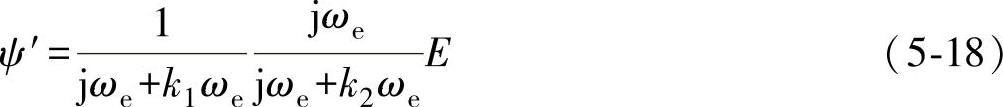
比较式（5-17）和式（5-18）得

ψ=ψ′（1-jk₁）（1-jk₂）=（ψ_α′+jψ_β′）（1-jk₁）（1-jk₂）=ψ_α+jψ_β （5-19）

因而

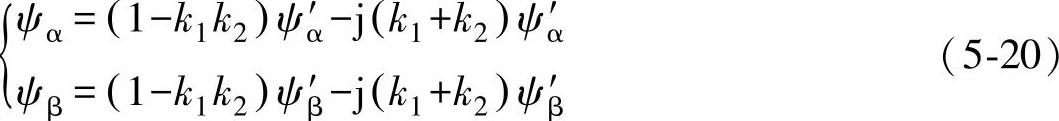
从而可根据式（5-20）改进的虚拟磁链获取框图如图5-16所示。

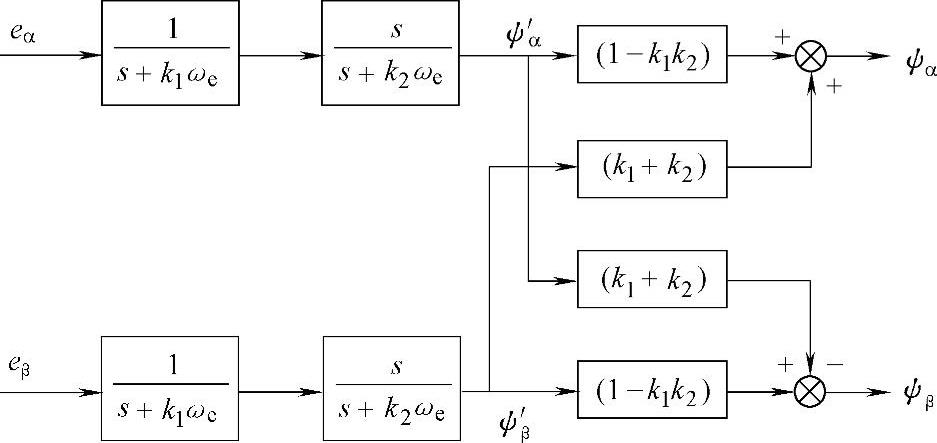
图5-16 改进算法的框图

改进后的效果如图5-15中的补偿后的波形，基本消除了稳态时与实际值之间存在相位和幅值偏差。