电压定向矢量控制（VOC）在电网中的应用

若同步旋转坐标系与电网电压矢量E同步旋转，且同步旋转坐标系的d轴与电网电压矢量E重合，则称该同步旋转坐标系为基于电网电压矢量定向的同步旋转坐标系。而基于电网电压定向的并网逆变器输出电流矢量图如图5-6所示。

显然，在电网电压定向的同步旋转坐标系中，有e_d=∣E∣，e_q=0。

根据瞬时功率理论（见5.3.1.1节），系统的瞬时有功功率p、无功功率q分别为

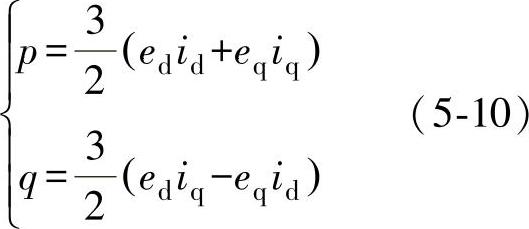
由于基于电网电压定向时，e_q=0，则式（5-10）可简化为

若不考虑电网电压的波动，即e_d为一定值，则由式（5-11）表示的并网逆变器的瞬时有功功率p和无功功率q仅与并网逆变器输出电流的d、q轴分量i_d、i_q成正比。这表明，如果电网电压不变，则通过i_d、i_q的控制就可以分别控制并网逆变器的有功、无功功率。

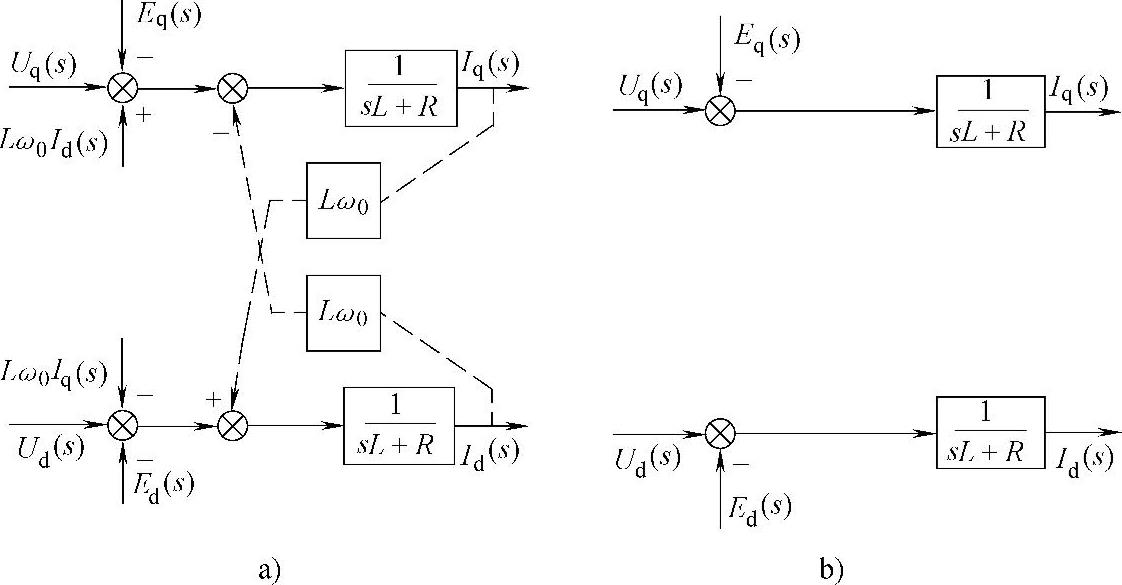
图5-5 引入前馈解耦的模型结构

a）前馈解耦引入的结构示意 b）解耦后的等效模型结构

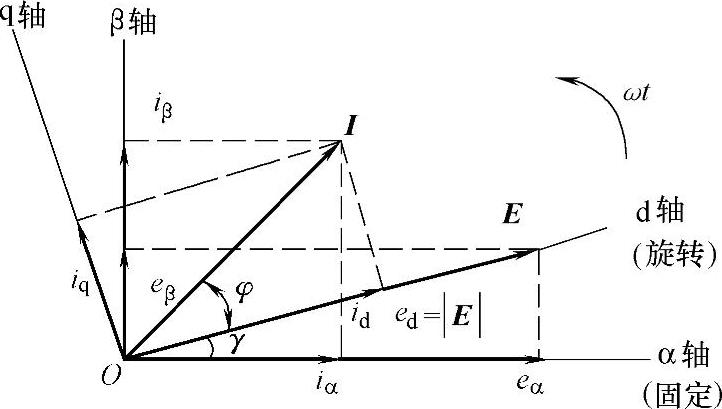
图5-6 基于电网电压定向的矢量控制（VOC）系统矢量图

在图5-1所示的并网逆变器中，直流侧输入有功功率的瞬时值为p=i_dcu_dc，若不考虑逆变器的损耗，则由式（5-11）可知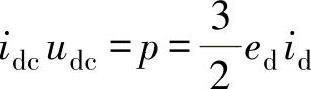：。可见，当电网电压不变且忽略逆变器自身的损耗时，并网逆变器的直流侧电压u_dc与并网逆变器输出电流的d轴分量i_d成正比，而并网逆变器的有功功率p又与i_d成正比，因此并网逆变器直流侧电压u_dc的控制可通过有功功率p即i_d的控制来实现。

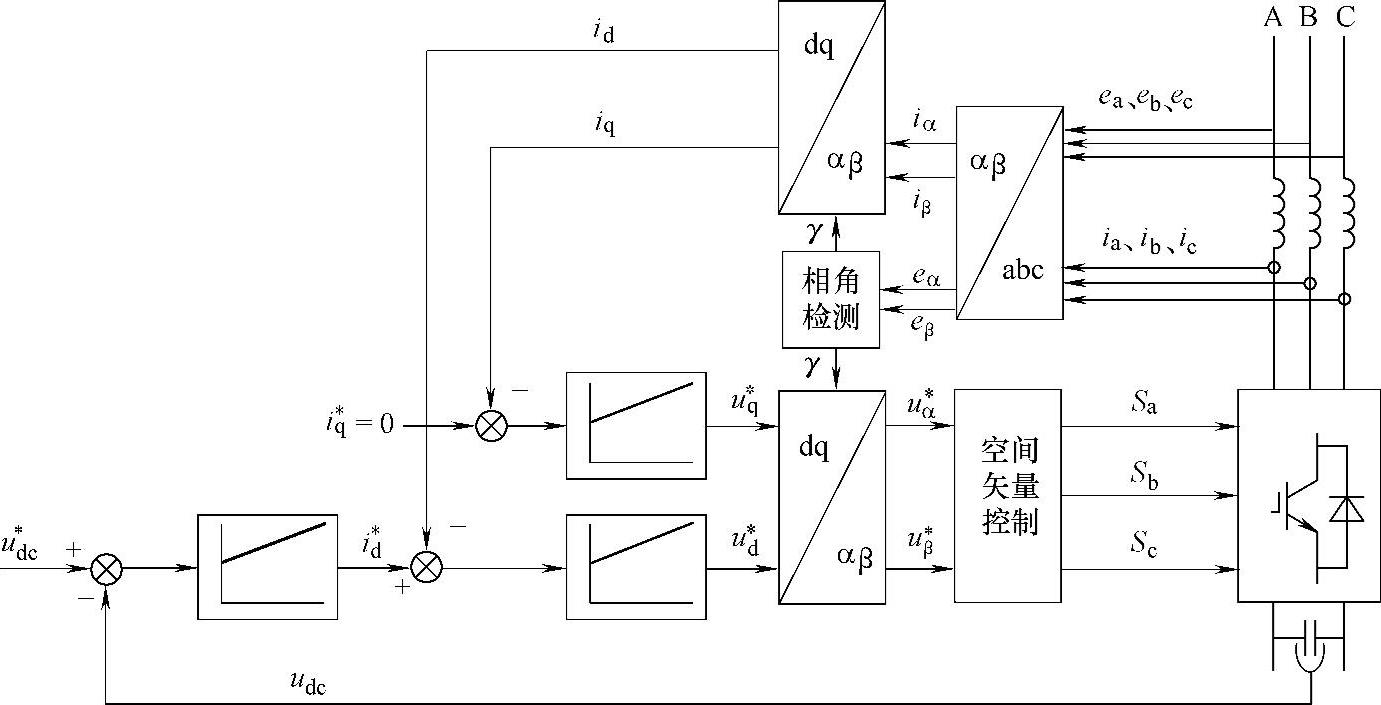
基于电网电压定向的并网逆变器的控制结构如图5-7所示。

(www.xing528.com)

图5-7 基于电压定向的矢量控制系统（VOC）示意图

控制系统由直流电压外环和有功、无功电流内环组成。直流电压外环的作用是为了稳定或调节直流电压，显然，引入直流电压反馈并通过一个PI调节器即可实现直流电压的无静差控制。由于直流电压的控制可通过i_d的控制来实现，因此直流电压外环PI调节器的输出量即为有功电流内环的电流参考值i_d^∗，从而对并网逆变器输出的有功功率进行调节。无功电流内环的电流参考值i_q^∗则是根据需向电网输送的无功功率参考值q^∗（由q^∗=e_di_q^∗运算）而得，当令i_q^∗=0时，并网逆变器运行于单位功率因数状态，即仅向电网输送有功功率。

电流内环是在dq坐标系中实现控制的，即并网逆变器输出电流的检测值i_a、i_b、i_c经过abc/αβ/dq的坐标变换转换为同步旋转dq坐标系下的直流量i_d、i_q，将其与电流内环的电流参考值i_d^∗、i_q^∗进行比较，并通过相应的PI调节器控制分别实现对i_d、i_q的无静差控制。电流内环PI调节器的输出信号经过dq/αβ逆变换后，即可通过空间矢量脉宽调制（SVPWM）得到并网逆变器相应的开关驱动信号S_a、S_b、S_c，从而实现逆变器的并网控制。

另外，图5-8中的坐标变换的相角信息γ是通过式（5-2）计算得到的，e_α、e_β值是通过检测电网电压（e_a，e_b，e_c）并经abc/αβ的坐标变换运算得到的。

若采用前馈解耦控制，且采用电网电压的前馈控制以补偿电网电压变化对系统控制的影响，解耦后的i_d电流内环控制结构如图5-8所示（i_q电流环与i_d电流环相同）。当开关频率足够高时，其逆变桥的放大特性可由比例增益K_PWM近似表示。

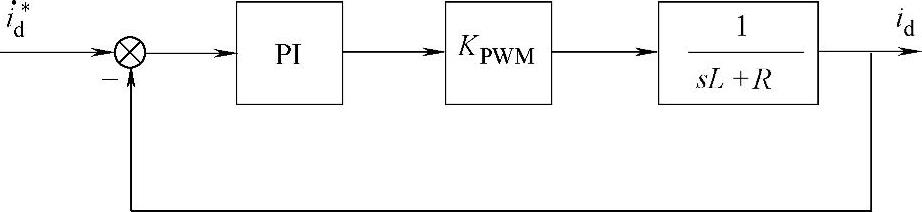
图5-8 电流内环控制结构

前面的分析表明，并网逆变器的直流电压是通过逆变器的有功功率p即有功电流i_d进行控制的，而又由图5-1分析易得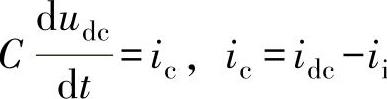：。因此要构建并网逆变器的直流电压外环，关键在于求得电流内环的输出i_d与逆变桥直流输入电流i_dc之间的传递关系。

实际上，由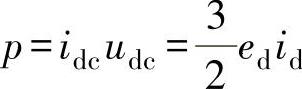，可得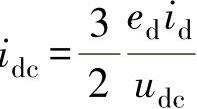，若令稳态时u_dc=U_DC，则

从而可得直流侧电压外环的控制结构，如图5-9所示。

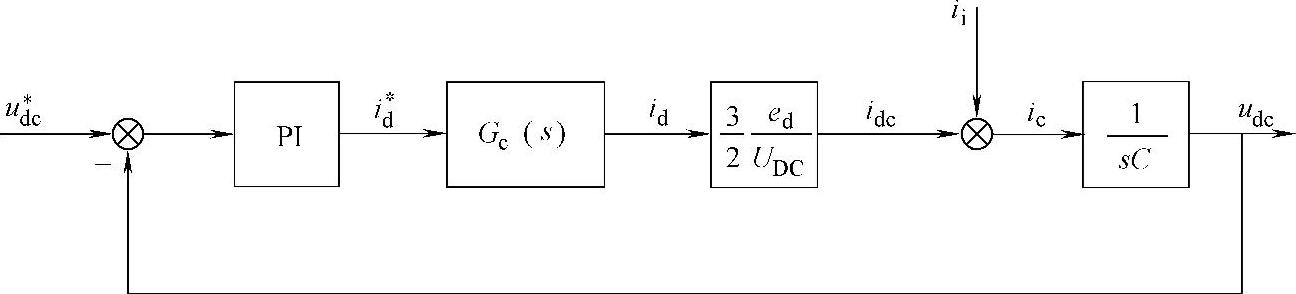
图5-9 直流侧电压外环控制结构

图中，G_c（s）表示电流内环的闭环传递函数。