同步坐标系下并网逆变器的数学模型优化

由图5-2分析，在三相静止abc坐标系下，并网逆变器的电压方程为

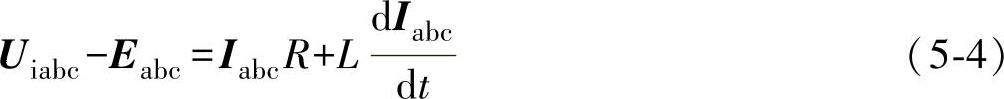
其中，令矢量X_abc=（x_a，xb，x_c）^T，x表示相应的物理量，下标表示abc坐标系中各相的变量，而X_abc∈（E_abc、U_iabc、I_abc）。

当只考虑三相平衡系统时，系统只有两个自由度，即三相系统可以简化成两相系统，因此可将三相静止abc坐标系下的数学模型变换成两相垂直静止αβ坐标系下的模型，即

X_βα=TX_abc （5-5）

式中 T——变换矩阵，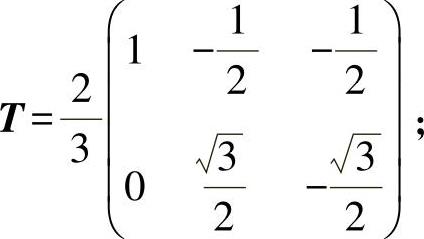

X_βα——矢量，X_βα=（x_β，xα）T。

显然，相应的逆变换可表示为X_abc=T^-1X_βα，将其代入式（5-4）并化简得

再将两相静止αβ坐标系下的数学模型变换成同步旋转dq坐标系下的数学模型，即

X_qd=T（θ）X_βα （5-7）

式中 T（θ）——变换矩阵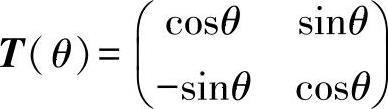，；(www.xing528.com)

X_qd——矢量，X_qd=（x_q，x_d）^T。

联立式（5-7）和式（5-6）并进行相应的数学变换可得

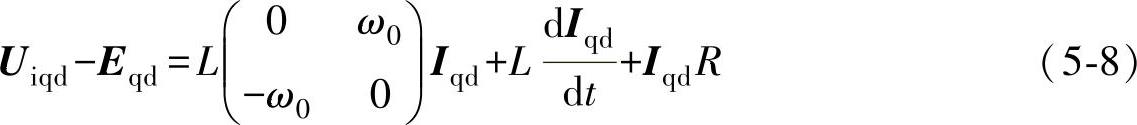
式中 ω₀——同步旋转角频率，且ω₀=dθ/dt。

在零初始状态下，对式（5-8）进行拉氏变换，可得到系统在同步旋转dq坐标系下并网逆变器频域的数学模型为

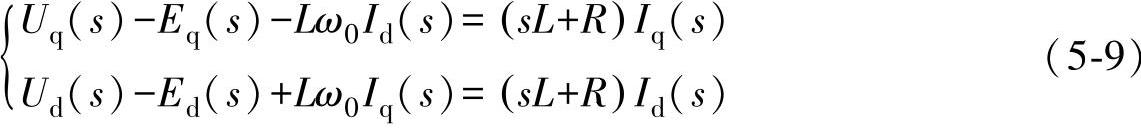
与式（5-9）相对应的模型结构如图5-4所示。

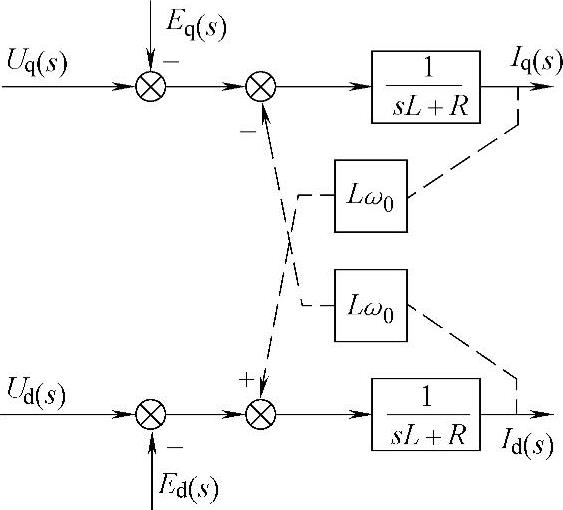
图5-4 系统在同步坐标系下的模型

显然，从图5-4可以看出，在dq坐标系中，并网逆变器的数学模型在d、q轴间存在耦合。为了实现dq轴的解耦控制，通常可以采用较为简单的前馈解耦策略，如图5-5所示，即在并网逆变器输出交流电压中分别引入前馈量+Lω₀I_d（s）和-Lω₀I_q（s），使其与图5-4模型中的耦合项-Lω₀I_d（s）和+Lω₀I_q（s）分别进行对消，从而实现了dq轴间的解耦，解耦后的系统模型转化为相互独立且完全对等的两部分，如图5-5b所示。前馈解耦实际上是一种开环解耦方案，其控制简单且不影响系统稳定性，然而这种前馈解耦的性能取决于系统参数，因而难以实现完全的解耦，实际上，前馈解耦是一种削弱耦合的补偿控制。