1.拉氏变换的定义
对于函数f（t），如果满足下列条件：
①当t＜0-时，f（t）=0；当t≥0-时，f（t）在每个有限区间上是分段连续的。
②
，其中σ为正实数，即f（t）为指数级的，则可定义f（t）的拉普拉斯变换（简称拉氏变换）F（s）为
②
，其中σ为正实数，即f（t）为指数级的，则可定义f（t）的拉普拉斯变换（简称拉氏变换）F（s）为
式中，s为复变数，f（t）为原函数，F（s）为像函数。
在拉氏变换中，s的量纲是时间的倒数，即[t]-1，F（s）的量纲则是f（t）的量纲与时间t量纲的乘积。
2.拉氏变换的性质
性质1（线性性质）设g（t）=af1（t）+bf2（t），则有
式中，s为复变数，f（t）为原函数，F（s）为像函数。
在拉氏变换中，s的量纲是时间的倒数，即[t]-1，F（s）的量纲则是f（t）的量纲与时间t量纲的乘积。
2.拉氏变换的性质
性质1（线性性质）设g（t）=af1（t）+bf2（t），则有
性质2（平移定理）设g（t）=f（t）e-at，则
性质2（平移定理）设g（t）=f（t）e-at，则
性质3（延时定理）设原函数在时间上延迟a（≥0），即有g（t）=f（t-a）·1（t-a），
性质3（延时定理）设原函数在时间上延迟a（≥0），即有g（t）=f（t-a）·1（t-a），
则
则
性质4（时间尺度定理）
若
性质4（时间尺度定理）
若
其中a＞0，则
其中a＞0，则
性质5（积分定理）
若
性质5（积分定理）
若
则有
则有
性质6（微分定理）
若
性质6（微分定理）
若
则
则
重复应用微分定理，可以得到高阶导函数的像函数。
若
重复应用微分定理，可以得到高阶导函数的像函数。
若
则重复应用微分定理n次就可得到
则重复应用微分定理n次就可得到
特别地，如果已知当t=0-时函数f（t）及其各阶导数均为0，则得到更简洁的公式
特别地，如果已知当t=0-时函数f（t）及其各阶导数均为0，则得到更简洁的公式
性质7（初值定理）利用拉氏变换可以求得原函数在t=0+的初值（注意不是t=0-的初值。按照拉氏变换的定义，在t从0-到0+的区间，原函数的值如发生幅度有限的跳变，不可能在像函数中得到反映），公式如下
性质7（初值定理）利用拉氏变换可以求得原函数在t=0+的初值（注意不是t=0-的初值。按照拉氏变换的定义，在t从0-到0+的区间，原函数的值如发生幅度有限的跳变，不可能在像函数中得到反映），公式如下
性质8（终值定理）如果原函数f（t）在t→∞时有极限存在，则此极限称为其终值，记作f（∞）。终值也可以利用拉氏变换求得，公式如下
性质8（终值定理）如果原函数f（t）在t→∞时有极限存在，则此极限称为其终值，记作f（∞）。终值也可以利用拉氏变换求得，公式如下
利用该性质，可在复域（s域）中计算系统在时间域中的稳态值，求系统的稳态误差。应注意，运用终值定理的前提是函数有终值存在，终值不确定则不能用终值定理。
例如，对于像函数F（s）=ω/（s2+ω2）就不能应用终值定理，事实上该函数的原函数为sinωt，在t→∞时终值不确定。
性质9（卷积定理）设当t＜0时，函数f1（t）和f2（t）均等于0，且有
利用该性质，可在复域（s域）中计算系统在时间域中的稳态值，求系统的稳态误差。应注意，运用终值定理的前提是函数有终值存在，终值不确定则不能用终值定理。
例如，对于像函数F（s）=ω/（s2+ω2）就不能应用终值定理，事实上该函数的原函数为sinωt，在t→∞时终值不确定。
性质9（卷积定理）设当t＜0时，函数f1（t）和f2（t）均等于0，且有
则称函数f（t）为函数f1（t）和f2（t）的卷积或褶积，常简记为
则称函数f（t）为函数f1（t）和f2（t）的卷积或褶积，常简记为
且可以证明有
且可以证明有
卷积定理：设f1（t）和f2（t）各自的拉氏变换分别为F1（s）和F2（s），则有
卷积定理：设f1（t）和f2（t）各自的拉氏变换分别为F1（s）和F2（s），则有
性质10 时间t乘函数后的拉氏变换。
若
性质10 时间t乘函数后的拉氏变换。
若
则
则
3.简单函数的拉氏变换
（1）单位阶跃函数1（t）的拉氏变换：
3.简单函数的拉氏变换
（1）单位阶跃函数1（t）的拉氏变换：
（2）指数函数eat·1（t）的拉氏变换：
（2）指数函数eat·1（t）的拉氏变换：
（3）正弦函数sinωt·1（t）和余弦函数cosωt·1（t）的拉氏变换。
根据欧拉公式，有
（3）正弦函数sinωt·1（t）和余弦函数cosωt·1（t）的拉氏变换。
根据欧拉公式，有
于是可以利用前面指数函数拉氏变换的结果，得出正弦函数和余弦函数的拉氏变换：
于是可以利用前面指数函数拉氏变换的结果，得出正弦函数和余弦函数的拉氏变换：
（4）幂函数tn·1（t）的拉氏变换。
可以利用Γ函数的性质得出结果。
（4）幂函数tn·1（t）的拉氏变换。
可以利用Γ函数的性质得出结果。
令u=st，则
令u=st，则
4.拉氏反变换(www.xing528.com)
拉氏反变换的公式为
4.拉氏反变换
拉氏反变换的公式为
简写为
简写为
它是复平面s上的积分，计算起来很困难，绝大多数情况下，工程上遇到的F（s）是有理函数，所以总是把它分解为部分分式，然后利用拉氏反变换表求出原函数。下面对部分分式展开法做简单介绍。
（1）F（s）只含不同单极点的情况：
它是复平面s上的积分，计算起来很困难，绝大多数情况下，工程上遇到的F（s）是有理函数，所以总是把它分解为部分分式，然后利用拉氏反变换表求出原函数。下面对部分分式展开法做简单介绍。
（1）F（s）只含不同单极点的情况：
式中，αk是常值，为s=-pk极点处的留数，αk可由下式求得
式中，αk是常值，为s=-pk极点处的留数，αk可由下式求得
将上式进行拉氏反变换，可得
将上式进行拉氏反变换，可得
【例A.1】试求F（s）=
的拉氏反变换。
【解】
【例A.1】试求F（s）=
的拉氏反变换。
【解】
（2）F（s）含共轭复数极点的情况：
（2）F（s）含共轭复数极点的情况：
式中，α1和α2是常数，由以下步骤求得：
将式（A.15）两边乘以（s+σ+jβ）（s+σ-jβ），同时令s=-σ-jβ（或同时令s=-σ+jβ），得
式中，α1和α2是常数，由以下步骤求得：
将式（A.15）两边乘以（s+σ+jβ）（s+σ-jβ），同时令s=-σ-jβ（或同时令s=-σ+jβ），得
分别令式（A.16）两端实、虚部相等，即可求得α1和α2，二者为共轭复数。
分别令式（A.16）两端实、虚部相等，即可求得α1和α2，二者为共轭复数。
可通过配方，化成正弦、余弦像函数的形式，然后求其反变换。
可通过配方，化成正弦、余弦像函数的形式，然后求其反变换。
【例A.2】试求F（s）=
的拉氏反变换。
【解】
【例A.2】试求F（s）=
的拉氏反变换。
【解】
将该式两边同乘s2+s+1，并令
将该式两边同乘s2+s+1，并令
含共轭复根的情况，也可用第一种情况的方法。
含共轭复根的情况，也可用第一种情况的方法。
【例A.3】求F（s）=
的拉氏反变换。
【解】
【例A.3】求F（s）=
的拉氏反变换。
【解】
（3）F（s）含多重极点的情况：
（3）F（s）含多重极点的情况：
式中，ar-j可由下式求得
式中，ar-j可由下式求得
根据拉氏变换表，有
根据拉氏变换表，有
据此，可求出含多重极点情况的拉氏反变换式。
据此，可求出含多重极点情况的拉氏反变换式。
【例A.4】求F（s）=
的拉氏反变换。
【解】
【例A.4】求F（s）=
的拉氏反变换。
【解】
5.用拉氏变换解线性微分方程
前面已介绍了描述控制系统运动特性的微分方程的建立方法，要想得到其时间特性，还需要把微分方程解出来。解微分方程有两种方法，一种是经典解法，另一种是用拉氏变换法求解。后一种方法比较简单，本节将举例说明线性常微分方程的拉氏变换解法及解中各分量的物理意义。线性常微分方程的拉氏变换解法步骤如下：
（1）考虑初始条件，对微分方程中的每项分别进行拉氏变换，将微分方程转换为变量s的代数方程；
（2）由代数方程求出输出量拉氏变换函数的表达式；
（3）对输出量拉氏变换函数求反变换，得到输出量的时域表达式，即为所求微分方程的解。
【例A.5】若描述系统输入、输出特性的微分方程为
5.用拉氏变换解线性微分方程
前面已介绍了描述控制系统运动特性的微分方程的建立方法，要想得到其时间特性，还需要把微分方程解出来。解微分方程有两种方法，一种是经典解法，另一种是用拉氏变换法求解。后一种方法比较简单，本节将举例说明线性常微分方程的拉氏变换解法及解中各分量的物理意义。线性常微分方程的拉氏变换解法步骤如下：
（1）考虑初始条件，对微分方程中的每项分别进行拉氏变换，将微分方程转换为变量s的代数方程；
（2）由代数方程求出输出量拉氏变换函数的表达式；
（3）对输出量拉氏变换函数求反变换，得到输出量的时域表达式，即为所求微分方程的解。
【例A.5】若描述系统输入、输出特性的微分方程为
式中，y（t）为输出量，x（t）为输入量，并且x（t）=1（t），其初始条件为y（0-）=-1，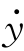
（0-）=4，试求其时间解。
【解】对方程（A.17）两端取拉氏变换有
式中，y（t）为输出量，x（t）为输入量，并且x（t）=1（t），其初始条件为y（0-）=-1，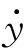
（0-）=4，试求其时间解。
【解】对方程（A.17）两端取拉氏变换有
整理得
整理得
上式代入初始条件可得
上式代入初始条件可得
把上式分解成部分分式
把上式分解成部分分式
式中
式中
把上面的系数代回原式，得
把上面的系数代回原式，得
式（A.18）中前三项称为零状态响应，它表示在初始条件为零情况下，输入信号加入后系统输出量的运动规律。这个规律和输入信号的形式有关，也和描述系统的微分方程有关，即和系统的结构、参数有关。
式（A.18）中后两项称为零输入响应，它表示在输入信号加入以前，系统存储的能量在信号加入以后的释放规律，这个规律取决于系统的结构和参数，其大小取决于初始条件。
另外，式（A.18）的第一项称为受迫分量或稳态分量，它表示在输入信号作用下，系统达到平衡状态以后的运动规律。这个规律取决于输入信号的形式，其大小和系统的结构参数有关。受迫分量对应经典解法中非齐次方程的特解。
式（A.18）中第二、三项与第四、五项中的相同函数可以合并，合并之后称为自由分量或暂态分量，其变化规律取决于系统的结构和参数，其大小和输入信号及初始条件有关。自由分量对应经典解法中齐次方程的通解，即对象自由运动的模态完全取决于微分方程的特征多项式。
式（A.18）中前三项称为零状态响应，它表示在初始条件为零情况下，输入信号加入后系统输出量的运动规律。这个规律和输入信号的形式有关，也和描述系统的微分方程有关，即和系统的结构、参数有关。
式（A.18）中后两项称为零输入响应，它表示在输入信号加入以前，系统存储的能量在信号加入以后的释放规律，这个规律取决于系统的结构和参数，其大小取决于初始条件。
另外，式（A.18）的第一项称为受迫分量或稳态分量，它表示在输入信号作用下，系统达到平衡状态以后的运动规律。这个规律取决于输入信号的形式，其大小和系统的结构参数有关。受迫分量对应经典解法中非齐次方程的特解。
式（A.18）中第二、三项与第四、五项中的相同函数可以合并，合并之后称为自由分量或暂态分量，其变化规律取决于系统的结构和参数，其大小和输入信号及初始条件有关。自由分量对应经典解法中齐次方程的通解，即对象自由运动的模态完全取决于微分方程的特征多项式。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
