基于Simulink的非线性控制系统数学仿真实验优化

实验目的：

验证采用描述函数法可以分析系统的稳定性，并求解稳定的自激振荡的振幅和频率。

实验预习：

已知含有饱和特性的非线性系统如图8.5.1所示，当K=15时，试用描述函数法分析非线性系统的稳定性；如果存在自激振荡，分析自激振荡的稳定性；如果自激振荡稳定，求其振幅和频率。进一步，欲使系统不出现自激振荡且稳定地工作，求K的最大容许值Kmax。

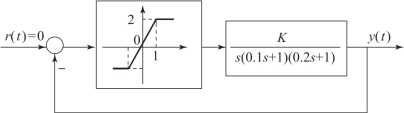
图8.5.1　某含有饱和特性的非线性系统(www.xing528.com)

实验：

实验1：在Simulink环境中描述如图8.5.1所示的非线性系统，在t=0 s时给系统加一个宽度为0.1、幅值为0.1的脉动函数作为输入信号，即在t=0 s时给系统一个幅值为0.1的阶跃激励，然后在t=0.1 s时撤掉这个信号，使得0.1 s后系统没有任何外作用。当线性环节增益分别为K=15、K=30时，画出非线性环节输入端和输出端，以及线性环节输出端的信号变化曲线。

实验2：如图8.5.1所示的非线性系统，输入信号改为单位阶跃信号，当K=3和K=6时，分别画出非线性环节输入端和输出端，以及线性环节输出端的信号变化曲线。

实验报告：

针对实验1，根据仿真曲线，给出当K=15、K=30时的自激振荡的振幅和频率，分析参数K对自激振荡的振幅和频率的影响规律。针对实验1和实验2，分析总结参数K对系统稳定性的影响规律。