自激振荡的稳定性分析

1.稳定的自激振荡定义

稳定的自激振荡是指系统受到轻微扰动后，偏离原来的运动状态，在扰动消失后，系统的运动能重新收敛于原来的等幅持续振荡状态。不稳定的自激振荡是指系统受扰动后，系统的运动不能重新收敛于原来的等幅持续振荡。

2.自激振荡分析

当系统中线性部分的频率特性G（jω）曲线与非线性元件的负倒描述函数-1/N（X）曲线相交时，可能产生自激振荡，那么这个自激振荡在扰动作用下是否能够稳定存在呢？现在讨论这个问题。

如图8.3.4所示，频率特性G（jω）曲线与负倒描述函数-1/N（X）交于A、B两点，A、B两点可能产生自激振荡。

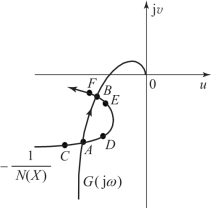
图8.3.4　存在周期运动的非线性系统

对于A点，G（jω）的频率为ωA，-1/N（X）的幅值为XA。如果系统受到扰动，使振荡幅值增加，则工作点由A点沿-1/N（X）曲线移动到D点，由于D点被G（jω）所包围，所以振荡幅值将继续增加，远离A点；如果系统受到扰动，使振荡幅值减小，则工作点由A点沿-1/N（X）曲线移动到C点，由于C点不被G（jω）曲线所包围，则振荡幅值将继续减小，直至为零。因此，A点为不稳定的自激振荡。不稳定的自激振荡观察不到。

对于B点，G（jω）的频率为ωB，非线性元件的负倒描述函数的幅值为XB。如果系统受到扰动幅值增加时，工作点将由B点沿-1/N（X）曲线移动到F点，由于F点不被G（jω）曲线所包围，所以振荡幅值减小，回到B点；如果系统受到扰动振幅减小时，工作点将由B点沿-1/N（X）曲线移动到E点，由于E点被G（jω）曲线所包围，故振荡将增幅，回到B点。因此B点是稳定的自激振荡点。稳定的自激振荡可以被观察到。

由上述讨论可得如下结论：若在线性部分的频率特性G（jω）曲线与非线性元件的负倒描述函数-1/N（X）曲线的交点处，沿振幅X增加的方向，-1/N（X）上的点不被G（jω）曲线所包围，则这个交点是稳定的自激振荡点。自激振荡的振荡频率为交点处G（jω）的ω值，振荡幅值为交点处-1/N（X）曲线的X值。

另外，对于图8.3.4所示情况，如果初始振荡的幅值小于XA，如在C点，则振荡会自动消失，系统是稳定的；如果大于XA，如在D点，则振荡振幅会自动增加，最后稳定于B点，形成稳定的自激振荡，因此非线性系统的稳定性与初始条件有关，系统产生自激振荡是有条件的，此外还应注意到稳定的自激振荡只是对一定范围的扰动而言具有稳定性，当扰动较大时，系统将停振或发散至无穷。另外，应用描述函数法分析非线性系统的稳定性，都是建立在只考虑基波分量的基础之上的，实际上，系统中仍有一定量的高次谐波分量通过，因此系统的自激振荡并非纯正弦波。

【例8.3.1】若系统框图如图8.3.5所示，试求该系统能否产生稳定的自激振荡；如果产生，确定振荡的频率及幅值。

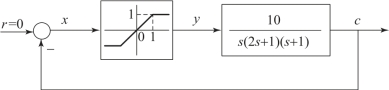
图8.3.5　例8.3.1的非线性系统方框图

【解】（1）绘制系统线性部分的幅相频率特性曲线。

由于系统中的饱和非线性特性的描述函数N（X）为正实数，故-1/N（X）为负实数，为了确定自激振荡，只需准确求出G（jω）与负实轴的交点，而其他部分可近似画出。系统线性部分的频率特性为

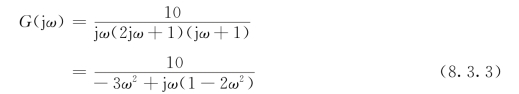
若G（jω）曲线与负实轴交点的频率为ω1，则有

把式（8.3.4）代入式（8.3.3），得G（jω）与负实轴的交点坐标为

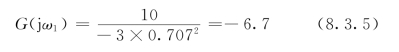
图8.3.6示出了G（jω）曲线。

（2）绘制饱和放大器非线性特性的负倒描述函数曲线。

根据表8.2.1中饱和特性的描述函数公式，令K=1，a=1，计算饱和放大器非线性特性的负倒描述函数数据列于表8.3.1，根据表8.3.1在图8.3.6上绘出-1/N（X）曲线。(www.xing528.com)

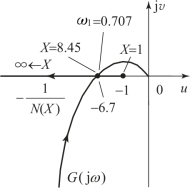
图8.3.6　例8.3.1系统的G（jω）和-1/N（X）曲线

表8.3.1　例8.3.1数据

（3）确定自激振荡及其稳定性。

由图8.3.6可知，G（jω）与-1/N（X）曲线在横轴-6.7处相交。当幅值X从交点处增加时，-1/N（X）曲线不被G（jω）曲线包围，所以系统产生自激振荡，而且自激振荡是稳定的，其振荡频率为0.707 rad/s，振荡幅值为X=8.45。

（4）讨论。

由图8.3.6可以看出，线性区增益等于1的饱和放大器的-1/N（X）曲线位于自（-1，j0）点之左的横轴上，如果G（jω）曲线不与负实轴相交或交于（-1，j0）点之右，则系统不会产生自激振荡。因此，按放大器线性区增益设计出的系统如果是稳定的，则信号进入放大器饱和区仍是稳定的。

图8.3.7给出了该系统自激振荡时饱和放大器输入端信号的时域响应曲线。

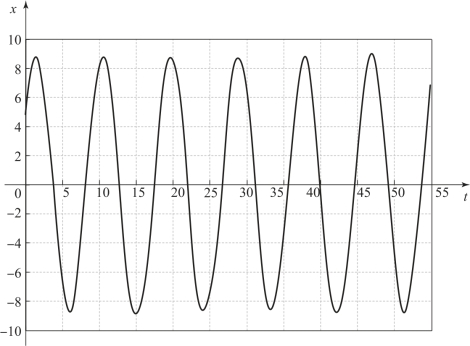
图8.3.7　例8.3.1系统中的自激振荡现象

【例8.3.2】若非线性系统框图如图8.3.8所示，图中2a=0.2，K=0.1，试确定该系统是否产生自激振荡；若产生自激振荡，则确定其频率和幅值。

图8.3.8　例8.3.2的系统框图

【解】（1）绘制G（jω）曲线。

若将-1/N（X）中的K值考虑到G（jω）中，可绘出KG（jω）的曲线，如图8.3.9所示。

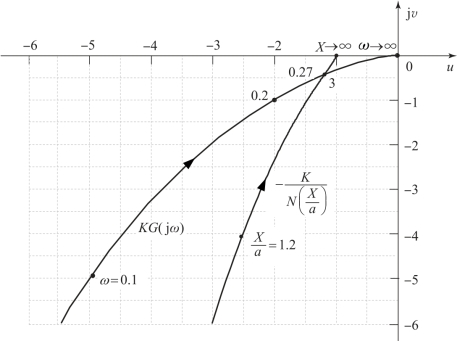
图8.3.9　例8.3.2系统的KG（jω）和-K/N（X）曲线

（2）绘制-1/N（X）曲线。

由于线性部分绘制的是KG（jω）曲线，所以负倒描述函数应画出-K/N（X）曲线。根据表8.2.1中间隙特性的描述函数公式和图8.3.8中非线性特性的参数，在图8.3.9上绘出-K/N（X/a）曲线。

（3）确定系统是否产生自激振荡及其稳定性。

由图8.3.9可以看出，KG（jω）曲线与曲线-K/N（X/a）有一个交点，系统可能产生自激振荡；由于在交点处沿X/a增加方向的-K/N（X/a）曲线不被KG（jω）所包围，故此自激振荡是稳定的，由交点处的数据查出自激振荡频率为ω=0.27 rad/s；相对幅值为X/a=3，题设a=0.1，所以X=3a=3×0.1=0.3。

（4）讨论。

本系统为二阶系统，若没有滞环非线性特性存在，当开环增益K＞0时，闭环系统总是稳定的。但是由于滞环系统的引入，使得自动控制系统产生了不希望的稳定等幅振荡。从步骤（3）得到的结果表明，自激振荡的幅值X与间隙2a成正比。因此在设计中应该限制传动装置的间隙。另外指出，因为实际系统有摩擦，而摩擦对自激振荡有一定的抑制作用，所以并不是所有系统传动装置有一点间隙就一定产生自激振荡。