离散串联校正设计对天线方位控制系统的优化

忽略功率放大器的动力学模型，并假设电位计的模型为1，可得到天线方位连续控制系统的简化框图如图7.8.2（a）所示。设计一个天线方位数字控制系统，如图7.8.2（b）所示，性能指标要求为调节时间不大于2 s（Δ=2%），系统阻尼系数为0.5，静态速度误差系数Kv=4。

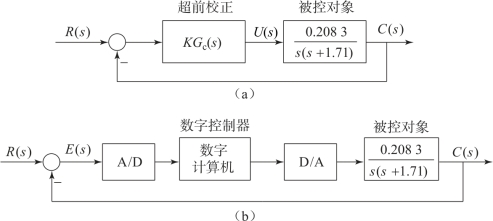
图7.8.2　天线方位控制系统的简化框图

（a）连续控制系统；（b）数字控制系统

【解】首先在频域内设计控制器，下面简单给出KGc（s）的设计过程。根据设计要求ts=2和ζ=0.5，得到期望系统的自然振荡频率为ωn=4/（ζts）=4 rad/s，相位裕度γ≈52°。

因为Kv=4，所以K=32.8。

未校正系统G（s）=的相位裕度为γ0≈36°、穿越频率ωc=2.35。

假设需要超前校正器提供的最大超前角为φmax≈23°，则α=2.3。

根据10lgα=3.6 dB，在G（s）的伯德图上找到-3.6 dB对应的频率为ωm=3 rad/s。则超前校正器的转折频率为ω1=1.96 rad/s，由于这个转折频率与原系统的转折频率非常接近，因此可以令ω1=1.71 rad/s，则ω2=4 rad/s。所以有

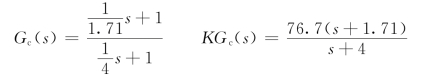
已校正系统的相位裕度为γ≈52°，穿越频率ωc=3.14 rad/s。

校正后闭环系统的带宽为ωb=5 rad/s，自然振荡频率ωn=4 rad/s，ζ=0.5，调节时间为2 s，满足了设计要求。

按照采样频率ωs≥20ωb的原则，采样周期T应该小于0.06 s，我们选一个较小值T=0.025 s。

利用Tustin变换，得到离散超前校正器(www.xing528.com)

如果在图7.8.2（b）中前向通路中串联零阶保持器，并对被控对象和零阶保持器一起进行z变换，采样周期为T=0.025 s，则得到

天线方位数字控制系统的单位阶跃响应如图7.8.3所示，系统的超调量约为18.35%，调节时间为2.1 s。

图7.8.3　带超前校正的闭环离散控制系统的单位阶跃响应（注意：仅在采样时刻有值）

定义KGc（z）=U（z）/E（z），则

得到U（z）上z的最高次幂

解得U（z）为

上式可以用来编写控制器的计算机实现程序。