【摘要】:图7.8.1所示的导弹通过弹体舵面的偏转产生力矩来进行气动控制,舵偏角指令来自一台计算机,计算机基于导弹制导律产生的加速度指令与导弹实际机动加速度的偏差来控制导弹按期望弹道飞行。图7.8.1导弹数字控制系统导弹;系统工作原理方框图;系统结构图;等效系统控制系统中的计算机可以用采样器和保持器进行建模,因此,系统的数学模型如图7.8.1所示,图7.8.1是其等效模型。
图7.8.1(a)所示的导弹通过弹体舵面的偏转产生力矩来进行气动控制,舵偏角指令来自一台计算机,计算机基于导弹制导律产生的加速度指令与导弹实际机动加速度的偏差来控制导弹按期望弹道飞行。图7.8.1(b)所示为控制系统工作原理方框图,导弹的加速度计检测实时加速度,并反馈给计算机。试计算该系统的闭环脉冲传递函数,并确定系统在K=20和K=100时系统是否稳定,其采样周期T=0.1 s。
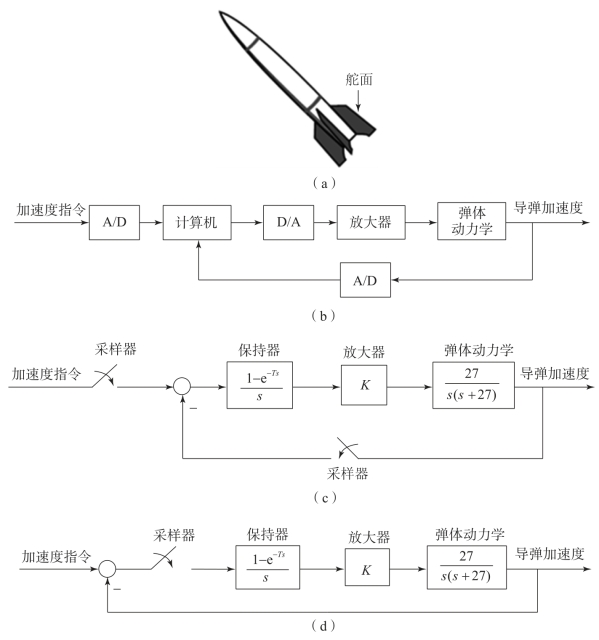
图7.8.1 导弹数字控制系统
(a)导弹;(b)系统工作原理方框图;(c)系统结构图;(d)等效系统
【解】控制系统中的计算机可以用采样器和保持器进行建模,因此,系统的数学模型如图7.8.1(c)所示,图7.8.1(d)是其等效模型。
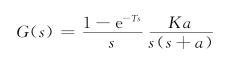
其中,a=27,进行z变换得
![]()
首先用因式分解对Ka/[s2(s+a)]进行展开,有(https://www.xing528.com)
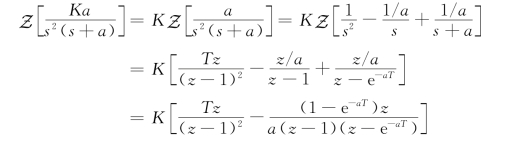
因此有
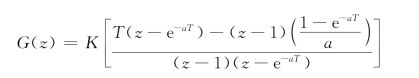
令T=0.1,a=27,有
![]()
最后,得到系统的闭环脉冲传递函数Φ(z):
![]()
通过求特征方程的根判断系统的稳定性,当K=20时,分母的根为0.12±j0.78,由于极点都在单位圆内,因此系统是稳定的。当K=100时,极点为-0.58和-4.9,由于其中一个极点在单位圆外,因此系统是不稳定的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




