离散系统动态性能的优化技巧

离散控制系统的动态性能，可以通过求解单位阶跃响应，获得系统的性能指标来进行分析。用z变换分析离散控制系统的时间响应与用拉氏变化法分析连续系统的时间响应相似。根据闭环脉冲传递函数和单位阶跃输入信号，求出系统的单位阶跃响应c*（t）。根据c*（t），可按照定义求出超调量、调节时间等性能指标。关于这些性能指标的定义，与连续系统是完全一样的。但应当指出的是，由于离散控制系统的时域性能指标只能按采样周期的整数倍处的采样值来计算，因此是近似的。

设离散系统的结构图如图7.6.1所示。图中Go（s）和Gh（s）分别为被控对象与零阶保持器的传递函数。假定采样周期T=1 s。

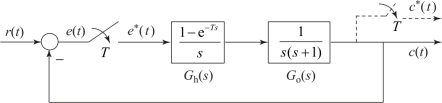
图7.6.1　离散系统结构图

因为保持器与被控对象之间没有采样开关，所以系统的闭环脉冲传递函数为

其中

进行z变换，并将T=1 s代入，得

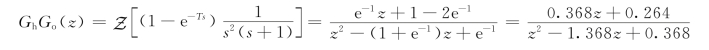
因此求得

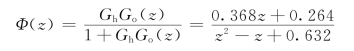
系统输出的z变换为

因为r（t）=1（t），所以R（z）=z/（z-1），代入上式，求得系统输出的z变换为

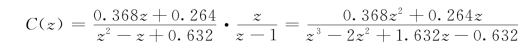
用综合除法进行幂级数展开，得

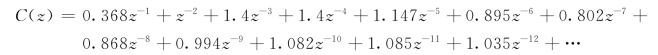
取C（z）的z反变换，求得系统的单位阶跃响应序列值为

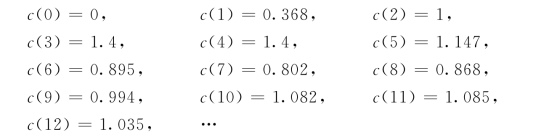
根据这些系统输出在采样时刻的值，可以大致描绘出系统单位阶跃响应的近似曲线（因为不能确定采样时刻之间的输出值），如图7.6.2所示。(www.xing528.com)

从图7.6.2中可以看出，系统的过渡过程具有衰减振荡的形式。输出的峰值发生在阶跃输入后的第三、四拍之间，最大值cmax≈c（3）=c（4）=1.4。由此可得出响应的最大超调量为

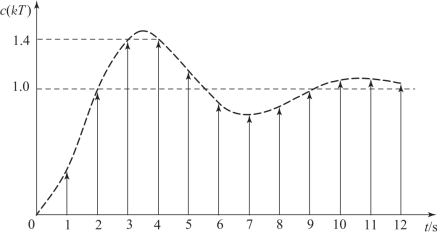
图7.6.2　系统单位阶跃响应曲线（T=1 s）

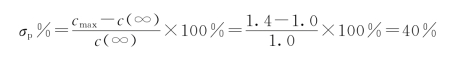
调节时间为

因为此系统为单位反馈系统，所以有

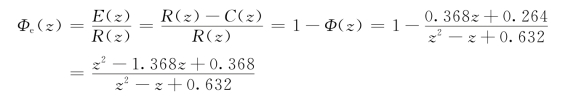
由此求得误差信号的z变换为

应用z变换的终值定理，可以求得系统在阶跃输入信号作用下的稳态误差为

由此可见，用z变换法分析离散系统的过渡过程，求取一些性能指标是很方便的。

当T=0.5 s时，系统的单位阶跃响应曲线如图7.6.3所示。

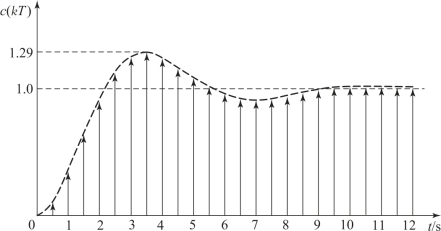
图7.6.3　系统单位阶跃响应曲线（T=0.5 s）

当T=2 s时，系统的单位阶跃响应曲线如图7.6.4所示。

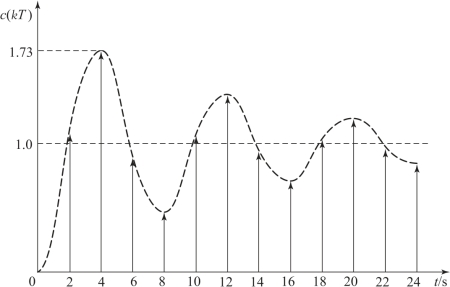
图7.6.4　系统单位阶跃响应曲线（T=2 s）

可见，采样周期对系统的动态性能影响很大。采样周期过大时，系统将由稳定系统变为不稳定系统。