稳态误差是离散系统分析和设计的一个重要指标,用离散系统理论分析的稳态误差仍然是指采样时刻的值。由于离散控制系统的脉冲传递函数与采样开关的配置有关,没有统一的公式可用,故通常采用终值定理计算稳态误差。只要系统的特征根全部位于z平面的单位圆内,即若离散系统是稳定的,则可用z变换的终值定理求出采样时刻的稳态误差。
设单位反馈离散控制系统的结构图如图7.5.5所示。G(s)是系统连续部分的传递函数,e(t)为连续误差信号,e*(t)为采样误差信号。
系统的误差脉冲传递函数为

图7.5.5 单位反馈离散系统
![]()
由此可得误差信号的z变换为
![]()
假定系统是稳定的,即Φe(z)的全部极点均在z平面的单位圆内,则可用终值定理求出稳态时采样时刻处的稳态误差为
![]()
下面分别讨论3种典型输入信号作用下系统的稳态误差。
1.单位阶跃输入信号作用下的稳态误差
由r(t)=1(t),可得
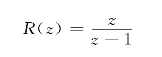
将此式代入式(7.5.6),得稳态误差为
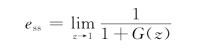
与连续系统类似,定义
![]()
为静态位置误差系数,则稳态误差为
![]()
从Kp定义式中可以看出,当G(z)中有一个以上z=1的极点时,Kp=∞,则稳态误差为零。也就是说,系统在阶跃输入信号作用下,系统无差的条件是G(z)中至少要有一个z=1的极点。
2.单位斜坡输入信号作用下的稳态误差
由r(t)=t,可得

将此式代入式(7.5.6),得稳态误差为

定义
![]()
为静态速度误差系数,则稳态误差为
![]()
从Kv定义式中可以看出,当G(z)中有两个以上z=1的极点时,Kv=∞,则稳态误差为零。也就是说,系统在斜坡输入信号作用下,系统无差的条件是G(z)中至少要有两个z=1的极点。
3.单位抛物线输入信号作用下的稳态误差
由r(t)=![]() ,可得
,可得

将此式代入式(7.5.6),得稳态误差为
 (https://www.xing528.com)
(https://www.xing528.com)
定义
![]()
为静态加速度误差系数,则稳态误差为
![]()
从Ka定义式中可以看出,当G(z)中有3个以上z=1的极点时,Ka=∞,则稳态误差为零。也就是说,系统在抛物线函数输入信号作用下,无差的条件是G(z)中至少要有3个z=1的极点。
从前面的分析中可以看出,离散系统采样时刻处的稳态误差与输入信号的形式、开环脉冲传递函数G(z)中z=1的极点数目以及采样周期T有关。G(z)中z=1的极点数就是系统的类型ν,对于G(z)中z=1的极点数为0、1、2、…、ν的离散系统,分别称为0、Ⅰ、Ⅱ、…、ν型系统。
总结前面讨论的结果,列成表7.5.1。从表中可以看出,高散系统的稳态误差除了与采样周期T有关外,其他规律与连续系统相同。
表7.5.1 采样时刻处的稳态误差

【例7.5.4】离散系统的方框图如图7.5.6所示,其中K=1。设采样周期T=0.1 s,试确定系统分别在单位阶跃、单位斜坡和单位加速度函数输入信号作用下的稳态误差。
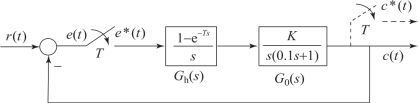
图7.5.6 例7.5.4的系统框图
【解】系统的开环传递函数为

系统的开环脉冲传递函数为
![]()
为应用终值定理,必须判别系统是否稳定,否则求稳态误差没有意义。
系统闭环特征方程为
![]()
即
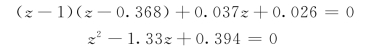
求得特征根z1=0.885,z2=0.445,所以系统是稳定的。
静态位置误差系数为
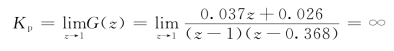
静态速度误差系数为
![]()
静态加速度误差系数为
![]()
不同输入信号作用下的稳态误差为:
单位阶跃输入信号作用下
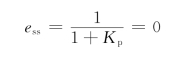
单位斜坡输入信号作用下

单位加速度输入信号作用下
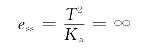
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




