离散系统稳定性的判据方法

连续系统中的劳斯判据是判别根是否全部在左半s平面，从而确定系统的稳定性。而在z平面内，稳定性取决于根是否全部在单位圆内。因此劳斯判据是不能直接应用的，如果将z平面再复原到s平面，则系统的方程中又将出现超越函数。所以我们需要寻找一种新的变换，将z平面上的单位圆映射为新坐标系的虚轴，而圆内部分映射为新坐标系的左半平面，圆外部分映射为新坐标系的右半平面，这种坐标变换称为双线性变换，亦称为w变换，相应的新的平面称为w平面，在此平面上，我们就可直接应用劳斯稳定判据了。

做双线性变换

则有

其中z、w均为复变量，写作

将式（7.5.4）代入式（7.5.3），并将分母有理化，整理后得

w平面的实部为

w平面的虚轴对应于u=0，则有

即

式（7.5.5）为z平面中的单位圆方程。若极点在z平面的单位圆内，则有x2+y2＜1，对应于w平面中的u＜0，即虚轴以左；若x2+y2＞1，则为z平面的单位圆外，对应于w平面中的u＞0，就是虚轴以右，如图7.5.3所示。

利用上述变换，可以将闭环离散系统的特征方程D（z）=0，转换成D（w）=0，然后就可直接应用连续系统中所介绍的劳斯稳定判据来判别离散系统的稳定性。

【例7.5.2】设离散系统的闭环特征方程为

图7.5.3　由z平面到w平面的映射

试用劳斯判据判别系统的稳定性。

【解】将(www.xing528.com)

代入特征方程得

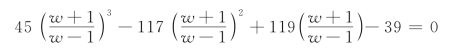
两边乘（w-1）3，化简后得

列出劳斯行列表为

因为第一列元素有两次符号改变，所以系统不稳定。正如连续系统中介绍的那样，劳斯判据还可以判断出有多少个根在右半平面。本例有两次符号改变，即有两个根在w右半平面，也即有两个根在z平面的单位圆外。

【例7.5.3】针对图7.5.4所示系统，当K=10时，确定使系统稳定的采样周期T的范围。当采样周期分别为T=0.1 s和T=0.15 s时，确定使系统稳定的K值，K＞0。

图7.5.4　例7.5.3的离散系统

【解】由于H（s）=1，可得闭环系统的z变换为

为了得到G（z），首先对G（s）进行因式分解：

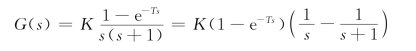
进行z变换，有

因此

当K=10时，其极点为11e-T-10，所以当0＜T＜0.2时系统稳定。

若T=0.1 s，其极点为0.905（K+1）-K，则当K＜20时系统稳定。

若T=0.15 s，其极点为0.860 7（K+1）-K，则当K＜13.3时系统稳定。

从上面的例子可以看出，采样周期对系统的稳定性是有影响的，这是连续系统与离散系统的显著区别。采样周期越长，系统的稳定域越小，对离散系统的稳定性和动态性能均不利，甚至可使系统不稳定。