离散系统稳定的充分必要条件解析

连续线性系统稳定的充要条件是闭环系统特征方程的根全部位于左半s平面上。而在线性离散系统中，稳定性是由闭环脉冲传递函数的极点在z平面上的分布确定的，应该用z平面来判断其稳定性。因此，需要分析s平面和z平面之间存在的映射关系，以便用连续系统的稳定判据来分析离散系统的稳定性。

s平面和z平面之间的映射关系为：

如果将复变量s=σ+jω代入上式，则有

所以

s平面上每一块区域通过式（7.5.1）都可以映射到z平面的相应区域。

设复变量s在s平面上沿虚轴取值，即s=jω，对应的z=ejωT，它是z平面上幅值为1的单位向量，其幅角为ωT，随ω而改变。因此，s平面上的虚轴在z平面上的映射是以原点为圆心的单位圆。

当s位于s平面虚轴左侧时，σ＜0，这时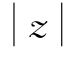＜1，此时s在z平面上的映射点位于以原点为圆心的单位圆内；若s位于s平面虚轴右侧时，σ＞0，这时＞1，此时s在z平面上的映射点位于以原点为圆心的单位圆外。可见，s平面左半部分在z平面上的映射为以原点为圆心的单位圆的内部区域，如图7.5.1所示。

图7.5.1　z平面与s平面的映射关系

由此可以得到离散控制系统稳定的充分必要条件是：系统特征方程的根，即闭环极点必须都分布在z平面上以原点为圆心的单位圆内。只要有一个特征根在以原点为圆心的单位圆外，离散控制系统就不稳定；若系统闭环特征方程在单位圆上有重根，系统也不稳定；当闭环特征方程只有一个单根在单位圆上，而其他根都在单位圆内时，则闭环系统临界稳定，在工程上通常将临界稳定视为不稳定情况。

而线性定常离散系统为BIBO稳定的充分必要条件是，闭环系统脉冲传递函数极点均分布在z平面的单位圆内。

【例7.5.1】图7.5.2所示系统中，设采样周期T=1 s，试分析当K=10和K=1时系统的稳定性。

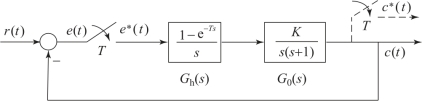
图7.5.2　例7.5.1的系统框图

【解】系统连续部分的传递函数为(www.xing528.com)

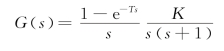
则当T=1时，

所以，系统的闭环脉冲传递函数为

系统的闭环特征方程为

将K=10代入方程，得

解得

z1、z2均在单位圆外，所以系统是不稳定的。

将K=1代入闭环特征方程，得

解得

z1、z2均在单位圆内，所以系统是稳定的。