脉冲传递函数简介

1.脉冲传递函数的定义

设开环离散系统如图7.4.1所示，在零初始条件下，线性定常离散系统的离散输出采样信号的z变换与离散输入采样信号z变换之比，称为该系统的脉冲传递函数（或z传递函数），记作

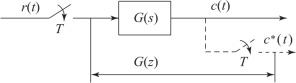
图7.4.1　开环离散系统

其中，R（z）、C（z）分别是离散系统输入离散信号和输出离散信号的z变换，即R（z）=。

所谓零初始条件，是指在t＜0时，输入脉冲序列各采样值及输出脉冲序列各采样值均为零。

式（7.4.3）表明，如果已知R（z）和G（z），则在零初始条件下，线性定常离散系统的输出采样信号为

由于R（z）是已知的，因此求c*（t）的关键在于求出系统的脉冲传递函数G（z）。

然而，对大多数实际系统来说，其输出往往是连续信号c（t），而不是采样信号c*（t），如图7.4.1所示。此时，可以在系统输出端虚设一个理想采样开关，如图中虚线所示，它与输入采样开关同步工作，并具有相同的采样周期。如果系统的实际输出c（t）比较平滑，且采样频率较高，则可用c*（t）近似描述c（t）。必须指出，虚设的采样开关是不存在的，它只表明脉冲传递函数所能描述的只是输出连续信号c（t）的采样信号c*（t）。

2.脉冲传递函数的含义

对于连续系统，当其输入为单位脉冲函数，即r（t）=δ（t）时，其输出为单位脉冲响应g（t）。对于如图7.4.1所示的离散控制系统，设其输入的采样信号为

根据叠加原理，系统的输出响应为

当t=kT时，可得

因为

所以

(www.xing528.com)

令m=k-n，则

由单位脉冲函数的特点可知，当t＜0时，g（t）=0。当n＞0时，m+n=0对应的m值都为负，因此上式可以写为

脉冲传递函数G（z）即为系统单位脉冲响应的采样信号g*（t）的z变换。

3.脉冲传递函数的求法

连续系统或元件的脉冲传递函数G（z），可以通过其传递函数G（s）来求取。方法是：先求G（s）的拉氏反变换，得到脉冲响应函数g（t）；再将g（t）按采样周期离散化，得到加权序列g（nT）；最后将g（nT）进行z变换，得出G（z）。

其实如果把z变换表7.3.1中的时间函数e（t）看成g（t），则表中的E（s）就是G（s），而E（z）相当于G（z），因此通过z变换表7.3.1，可以直接从G（s）得到G（z），而不必逐步推导。

【例7.4.3】开环系统中G（s）=，求系统的脉冲传递函数。

【解】将G（s）展开为部分分式

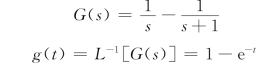
系统的脉冲传递函数为

在实际应用中，可以根据z变换表，直接从G（s）得到G（z），而不必逐步推导。如果G（s）为阶次较高的有理分式函数，则需将G（s）展成部分分式，使各部分分式对应的z变换都可以在表中查到。

习惯上，常把G（z）表示为G（z）=，并称之为G（s）的z变换，这时应理解为根据式（7.4.3）求解所得的G（z）。

如果描述线性定常离散系统的差分方程为

在零初始条件下，对上式进行z变换，并应用z变换实数位移定理，可得

相应的脉冲传递函数为

可见，差分方程和脉冲传递函数都是对系统物理特性的数学描述，它们虽然形式不同，但实质相同。