简单易懂的 z 反变换方法解析

在连续系统中，应用拉氏变换的目的，是把描述系统的微分方程转换为s的代数方程，然后写出系统的传递函数，即可用拉氏反变换法求出系统的时间响应，从而简化了控制系统的分析研究。与此类似，在离散系统中应用z变换，也是为了把s的超越方程或者描述离散系统的差分方程转换为z的代数方程，然后写出离散系统的脉冲传递函数（z传递函数），再用z反变换法求出离散系统的时间响应。

所谓z反变换，是已知z变换表达式E（z），求相应离散序列e（kT）的过程。z反变换可以记作

因为z变换只表征连续函数在采样时刻的特性，并不反映采样时刻之间的特性，所以z反变换只能求出采样函数e*（t）或e（kT），而不能求出连续函数e（t）。

求z反变换的方法通常有以下3种：部分分式法、幂级数法（综合除法）、反演积分法。在求z反变换时，仍假定当k＜0时，e（kT）=0。下面介绍最常用的两种求z反变换的方法。

1.部分分式法

部分分式法又称查表法。此法是将E（z）通过部分分式分解为低阶的分式之和，直接从z变换表中查出各项对应的z反变换，然后相加得到e（kT）。考虑到z变换表中，所有z变换函数E（z）在其分子上普遍都有因子z，所以应将E（z）/z展开为部分分式，然后将所得结果的每项都乘以z，即得E（z）的部分分式展开式。

大部分连续时间信号都是由基本信号组合而成的，而基本信号的z变换大都可以借用z变换表查得。

【例7.3.5】已知E（z）=，求e（kT）。

【解】由于E（z）中通常含有一个z因子，所以首先将式E（z）/z展成部分分式较容易些。

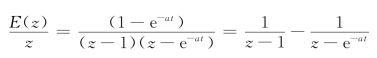
再求E（z）的分解因式

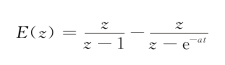
查z变换表7.3.1，得到

所以在采样瞬时相应的信号序列为

即(www.xing528.com)

2.幂级数法

幂级数法又称综合除法或长除法，即把式E（z）展开成按z-1升幂排列的幂级数。因为E（z）的形式通常是两个z多项式之比，即

所以，很容易用综合除法展成幂级数。对上式用分母去除分子，所得之商按z-1的升幂排列

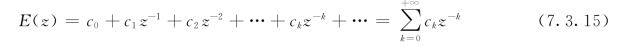
这正是z变换的定义式。z-k项的系数ck就是时间函数e（t）在采样时刻t=kT时的值。因此，只要求得上述形式的级数，就知道时间函数在采样时刻的函数值序列，即e（kT）。

【例7.3.6】试用长除法求E（z）=的z反变换。

【解】

进行综合除法运算

即

由上式的系数可知

在实际应用中，常常只需要计算有限几项就够了。用幂级数法计算e*（t）最简便，这是z变换法的优点之一。但是，要求出e*（t）的通项表达式，一般是比较困难的。