Z变换求解方法

1.级数求和法

级数求和法是直接根据z变换的定义，将E（z）=展开，根据无穷级数求和公式

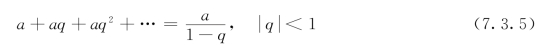
即可求出函数的z变换。通常，对于常用函数z变换的级数形式，都可以写出其闭合形式。

【例7.3.1】试求单位阶跃函数1（t）的z变换。

【解】由于e（t）=1（t）在所有采样时刻上的采样值均为1，即

由定义有

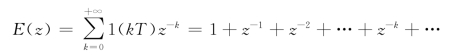
在上式中，若＜1时，则该无穷级数收敛，这时利用等比级数求和公式，可得z变换形式为

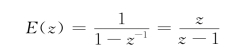
【例7.3.2】设e（t）=δT（t）=，试求理想脉冲序列δT（t）的z变换。

【解】由于T为采样周期，故

由拉氏变换知

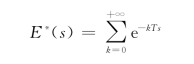
故

从例7.3.1和例7.3.2可以看出，相同的z变换E（z）对应于相同的采样函数e*（t），但是不一定对应于相同的连续函数e（t），这是利用z变换分析离散系统时特别要注意的一个问题。

2.部分分式法

利用部分分式法求z变换时，先求出已知连续时间函数e（t）的拉氏变换E（s），然后将有理分式函数E（s）展成部分分式之和的形式，使每一部分分式对应简单的时间函数，其相应的z变换是已知的，于是可方便地求出E（s）对应的z变换E（z）。(www.xing528.com)

【例7.3.3】已知E（s）=，求z变换。

【解】将E（s）按照它的极点展成部分分式

对上式逐项取拉氏反变换，可得

【例7.3.4】设e（t）=sinωt，试求其E（z）。

【解】对e（t）=sinωt取拉氏变换，得

将上式展开为部分分式为

根据指数函数的z变换表达式，可以得到

化简后得

常见时间函数的z变换如表7.3.1所示。由表可见，这些函数的z变换都是z的有理分式，且分母多项式的次数大于或等于分子多项式的次数。值得指出的是，表中各z变换有理分式中，分母z多项式的最高次数与相应传递函数分母s多项式的最高次数相等。

表7.3.1　z变换表

续表

续表