采样定理与被采样信号变化的关系

要对被控对象进行控制，通常要把采样信号恢复成连续信号，此工作一般是由低通滤波器来完成的。但是信号能否恢复到原来的形状，主要取决于采样信号是否包含反映原信号的全部信息。实际上这又与采样频率有关，因为连续信号经采样后，只能给出采样时刻的数值，不能给出采样时刻之间的数值，亦即损失掉了e（t）的部分信息。由图7.2.1可以直观地看出，连续信号变化越缓慢，采样频率越高，则采样信号e*（t）就越能反映原信号e（t）的变化规律，即越多地包含原信号的信息。采样定理则是定量地给出采样频率与被采样的连续信号的“变化快慢”的关系。下面首先分析采样前后信号频谱的变化。

1.采样信号的频谱与香农（Shannon）采样定理

首先将式（7.2.1）中的δT（t）展开成傅里叶级数

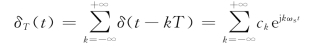
式中，ωs==2πfs，为采样角频率；fs为采样频率；T为采样周期；ck为傅氏级数的系数，由下式决定

由于δT（t）在-T/2到+T/2区间仅在t=0时有值，所以

故有

由式（7.2.1）可得

由拉氏变换的位移定理可得

于是，得到采样信号的频率特性为

(www.xing528.com)

式中，E（jω）为原输入信号e（t）的频率特性；E*（jω）为采样信号e*（t）的频率特性。

图7.2.3　信号的频谱

（a）连续信号频谱；（b）采样信号频谱（ωs＞2ωh）；（c）理想滤波器的频率特性；（d）采样信号频谱（ωs＜2ωh）

一般来说，连续信号e（t）的频谱为，是单一的连续频谱，如图7.2.3（a）所示，它的最高频率为ωh。采样信号e*（t）的频谱，是无限多个以采样频率ωs为周期的原信号e（t）的频谱之和，如图7.2.3（b）所示。其中k=0时，就是原信号的频谱，只是幅值为原来的1/T；而其余的是由于采样产生的高频频谱。如果中各个波形不重复搭接，相互间有一定的距离（频率），即若

则可以用理想低通滤波器（其频率特性如图7.2.3（c）所示）把ω＞ωh的高频分量滤掉，只留下部分，就能把原连续信号复现出来。否则，如果，就会使中各个波形互相搭接，如图7.2.3（d）所示，无法通过滤波器滤除E*（jω）中的高频部分，也就不能将e*（t）恢复为e（t）。

香农采样定理指出：如果采样器的输入信号e（t）具有有限带宽，并且有直到ωh的频率分量，则使信号e（t）圆满地从采样信号e*（t）中恢复出来的采样周期T，满足下列条件

式中，ωh为连续信号e（t）的最高次谐波的频率，采样定理表达式（7.2.12）与ωs≥2ωh是等价的。这就是说，如果选择的采样频率足够高，使得对连续信号所含的最高次谐波，能做到在一个周期内采样两次以上，那么经采样后所得到的脉冲序列，就包含了原连续信号的全部频谱信息，就有可能通过理想滤波器把原信号毫无失真地恢复出来。否则采样频率过低，信息损失很多，原信号就不能准确复现。

2.采样周期的选取

香农采样定理只是给出了采样周期选择的基本原则，并未给出选择采样周期的具体计算公式。显然，采样周期T选得越小，即采样频率ωs选得越高，对控制过程的信息便获得越多，控制效果也会越好。但是，采样周期T选得过小，将增加不必要的计算负担，造成实现较复杂控制规律的困难。而且采样周期T小到一定的程度后，再减小就没有多大实际意义了。反之，采样周期T选得过大，又会给控制过程带来较大的误差，降低系统的动态性能，甚至有可能导致整个控制系统失去稳定。

采样频率的选择依赖于系统的带宽，一般而言，采样频率应该是20倍的系统带宽，即ωs=20ωb，以便使离散控制器的性能与其对应的连续控制器的性能匹配。如果系统可以容忍因采样频率降低而导致的性能下降，那么也可以降低采样速率。但是，一般当ωs≥25ωb时，数字控制器的性能是比较好的。

Astrom和Wittenmark（1984）给出了采样周期T的选择方法，即T的数值应该在0.15/ωc到0.5/ωc秒之间，其中ωc是已校正系统的穿越频率。

根据经验，也可按照系统响应时间确定采样周期，即T=0.1Tmin，Tmin是系统中反应最快的子系统的最小时间常数。