采样过程及其数学描述

把连续信号变换为脉冲信号的装置称为采样器，又称为采样开关。采样器的采样过程，可以用一个周期性闭合的采样开关来表示，如图7.2.1所示。

图7.2.1　实际采样过程

对于实际采样过程，将连续信号e（t）加到采样开关的输入端，采样开关以周期T闭合一次，闭合的持续时间为τ，在闭合期间，截取被采样的e（t）的幅值，作为采样开关的输出。在断开期间采样开关的输出为零。于是在采样开关的输出端就得到宽度为τ的脉冲序列e*（t）（以“*”表示采样信号）。

对于具有有限脉冲宽度的采样系统来说，要准确进行数学分析是非常复杂的，且无此必要。考虑到采样开关的闭合时间τ非常小，通常为毫秒到微秒级，一般远小于采样周期T和系统连续部分的最小时间常数，因此在分析时，可以认为τ=0。这样，采样器就可以用一个理想采样器来代替。

在理想的采样过程中，连续信号经采样开关的周期采样后，得到的采样脉冲的强度等于连续信号在采样时刻的幅值。因此，理想采样开关可以视作一个脉冲调制器，采样过程可以视作一个单位脉冲序列δT（t）被输入信号e（t）进行幅值调制的过程，如图7.2.2所示。其中，单位脉冲序列δT（t）=δ（t-kT）为载波信号，e（t）为调制信号。

图7.2.2　幅值调制过程（采样过程）

假设当t＜0时，e（t）=0，因此脉冲序列从零开始，这个前提在实际控制系统中，通常都是满足的。因此当t≥0时，输出信号可表示为

式（7.2.1）为理想采样过程的数学表达式，其中δ（t-kT）是出现在t=k T、强度为1的单位脉冲。

考虑到δ函数的特点，式（7.2.1）可描述为

对采样信号e*（t）进行拉氏变换，可得

(www.xing528.com)

根据拉氏变换的位移定理，有

所以，采样信号的拉氏变换为

式（7.2.4）将E*（s）与采样函数e（kT）联系起来，e（kT）描述的是e*（t）在采样瞬时的值，所以E*（s）不能给出连续函数e（t）在采样间隔之间的信息。

【例7.2.1】设e（t）=e-at，t≥0，a为常数，试求e*（t）的拉氏变换。

【解】由式（7.2.4），有

式中，σ为s的实部。上式是eTs的有理函数。

【例7.2.2】设e（t）=e-t-e-2t，t≥0，试求采样拉氏变换E*（s）。

【解】

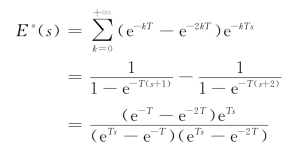
而连续信号e（t）的拉氏变换为

通过例题求解结果可以看出，用拉氏变换法研究离散系统，尽管可以得到eTs的有理函数，但它是一个复变量s的超越函数，不便于进行分析和设计。为了克服这一困难，通常采用z变换法研究离散系统。z变换可以把离散系统的s超越方程，变换为变量z的代数方程。有关z变换理论将在7.3节介绍。