使用灵敏度函数的性能指标与设计限制

对于典型的单位反馈控制系统，输入信号R作用下的误差为

式中正是反馈控制系统的灵敏度函数，G（jω）是被控对象的频率特性，Gc（jω）是控制器的频率特性，R是由某些特定频率的正弦信号叠加合成的实际系统输入信号。

从式（6.10.2）可见，灵敏度函数）是系统误差的乘数因子，大，系统误差就会被放大；灵敏度函数也是Gc（jω）G（jω）的奈奎斯特曲线与临界点（-1，j0）的距离的倒数，因此，的取值越大，表示Gc（jω）G（jω）的奈奎斯特曲线越接近（-1，j0）点，闭环系统就越接近不稳定。

根据图6.10.1中开环幅频曲线对系统性能指标的描述，可知低频段≥W1，所以

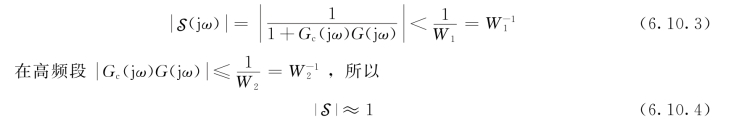
因此要想得到满意的反馈系统性能，在0≤ω≤ω1的频率范围内，应满足；要想使系统在高频段具有鲁棒性，在ω2≤ω的频率范围内，应满足≈1，这就是基于灵敏度函数的系统性能指标描述。

在前面我们说过，伯德提出了幅相定理，给出了频域内控制系统设计的重要约束条件。伯德的另一个突出贡献就是基于灵敏度函数提出了伯德积分定理。伯德积分将反馈系统的控制难度在频域内进行了量化，即伯德积分是反馈系统控制难度的一个量化指标，这个指标对控制系统设计约束的阐释非常深刻、朴实、简单、清晰，优于很多其他描述方法。每个控制理论学家或者控制工程师，都应该掌握伯德积分定理并深入理解它的含义。

伯德积分定理指出，反馈控制系统的的积分值在某些条件下是恒定不变的定值，类似守恒定律。Freudenberg和Looze在1985年发展了伯德的观点，Bing-Fei Wu在1992年进一步完善了伯德积分定理。

伯德积分定理：假设系统开环传递函数Gc（s）G（s）在右半s平面有np个极点pi，并且其开环对数幅频曲线在高频段以小于-20 dB/dec的斜率迅速下降，这对于有理式而言，意味着开环传递函数中有限极点的数目至少比零点的数目多两个，在此假设条件下，闭环系统灵敏度函数幅值的ln值（即ln）的积分是一个常值，即

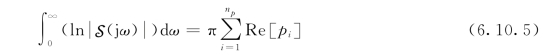
即ln的积分值是由Gc（s）G（s）在右半s平面的极点所决定的。

注意，我们讨论的是灵敏度函数幅值的ln值，因此，若ln是负值，意味着灵敏度函数的幅值小于1，因此，加入反馈后的闭环系统性能比开环系统好；若是正值，意味着灵敏度的幅值大于1，即加入反馈后的闭环系统性能还不如开环系统好。

下面分两种情况对伯德积分定理进行讨论。

1.开环系统稳定的情况

由式（6.10.5）可见，如果Gc（s）G（s）在右半s平面没有极点，即系统是开环稳定的，则的积分值为零。这意味着，如果在某个频率范围内，远远小于零，那么在另一个频率范围内，必然远远大于零，因此会放大系统在此频率段的误差，这种特点被称为“水床效应”（Water Bed Effect）。“水床效应”规则适用于所有的反馈控制系统，不管它的控制器是怎么被设计出来的，即系统在一个频段的灵敏度改善必然会被另一个频段的灵敏度恶化抵消掉，灵敏度的改善总是有代价的。举一个简单例子，若一单位反馈系统的开环传递函数为G1（s）=，则其闭环系统的随频率的变化曲线如图6.10.2所示。

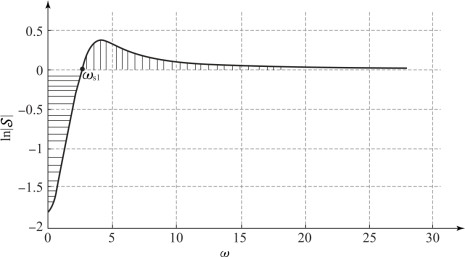
图6.10.2　ln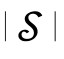随频率的变化曲线（G1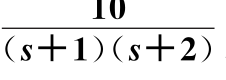（s）=）(www.xing528.com)

从图6.10.2可以看出，积分面积为正的区域与积分面积为负的区域相等，因此面积的和为零。当频率低于ωs1时，小于1，可以减小系统在这个频率范围内的误差；而在频率大于ωs1的频段内，大于1，从而会放大系统在这个频率范围内的误差。若增大系统的开环增益，例如G2（s）=，则其闭环系统的随频率的变化曲线如图6.10.3中的实线所示，图中虚线为开环增益K=10时（即G1（s））的曲线。

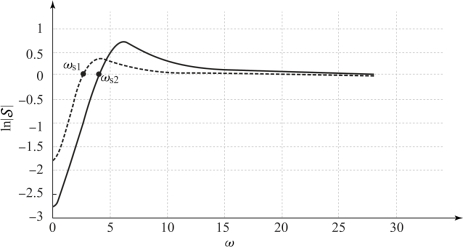
图6.10.3　ln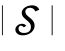随频率的变化曲线（G2（s）=）

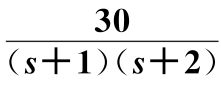由图6.10.3可见，K=30时，频率低于ωs1的闭环系统误差比K=10时降低了，但是频率高于ωs2的系统误差却增大了。

2.开环系统不稳定的情况

根据式（6.10.5），如果系统开环传递函数Gc（s）G（s）有不稳定极点，则积分面积为正的区域将比积分面积为负的区域大，因此对系统误差的放大作用要比对误差的减小作用大，这充分说明了相对于稳定的开环系统而言，不稳定开环系统的控制系统设计难度要大一些。例如一单位反馈系统的开环传递函数为G3（s）=，为开环不稳定系统，其随频率的变化曲线如图6.10.4中的实线所示，虚线对应开环传递函数为G1（s）时的曲线。从图中可以看出，积分面积为正的区域比积分面积为负的区域大了3.14，对频率高于ωs3的系统误差的放大作用比图6.10.2的开环稳定系统要大很多。另外，由于控制能量受限，开环不稳定的反馈控制系统只能是局域稳定的，而不可能是全局稳定的。

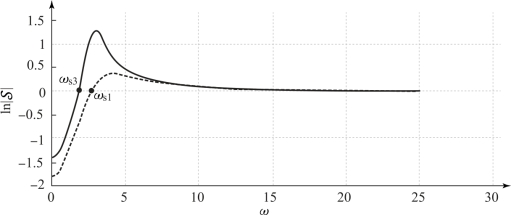
图6.10.4　ln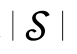随频率的变化曲线（G3（s）=）

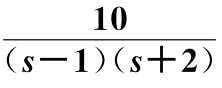由图6.10.2可见，针对最小相位系统，为了提高反馈控制系统在ωs1≤ω＜∞频段上的系统灵敏度性能，如果我们凭直觉使这部分的=ε，且ε非常小，即积分为正的这部分区域的厚度非常薄，相应的灵敏度函数的幅值就会非常小，可惜这是无法实现的。因为=ε成立的条件是开环系统Gc（s）G（s）的奈奎斯特曲线在ωs1≤ω≤∞的频段内，位于一个以（-1，j0）为圆心、以（1-ε）为半径的圆周附近。这意味着开环系统Gc（s）G（s）不能在高频处简单直接地进行幅值的衰减，而必须沿着一条非常精确的轨迹进行幅值衰减，这就需要开环系统在很宽的频率范围内具有很精确的频率特性，也就是说，要求控制系统模型在高频段也必须是非常准确的。但是被控对象在一定带宽范围之外的频率特性是不确定和不精确的，因为被控系统总是存在着不确定性、未建模动态、执行功率限制、非线性、控制器数字实现误差以及其他很多干扰因素。进一步，实际系统的可用带宽受制于反馈控制回路中各实际物理元部件的硬件性能，且可用带宽是有限的，因而不可能使灵敏度函数的幅值在ωs1≤ω＜∞的频段上都非常小。可用带宽的有限性是控制系统设计中非常重要的概念，其重要性远远超过非最小相位系统概念。

考虑系统可用带宽Ωa的限制，式（6.10.5）所示的伯德积分变为有限积分，积分范围为0≤ω≤Ωa，即

当开环系统稳定时，

当开环系统不稳定时，

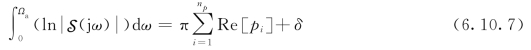
以上两式表明，在进行反馈控制系统设计时，灵敏度的改善和灵敏度的恶化，都必须在0≤ω≤Ωa这个频段内发生，只有很少的一点误差δ可以发生在这个频率范围之外，这个误差δ可正可负，系统设计要保证其绝对值很小。

灵敏度函数与系统的稳定程度密切相关，针对最小相位系统，在低于系统带宽的某个频率点上，灵敏度函数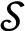会有一个有限的但可能很大的正值越大，意味着开环传递函数Gc（s）G（s）的奈奎斯特曲线越接近临界点（-1，j0），系统的矢量裕度VM就越小，其关系如下：

例如，针对G1（s）=，由图6.10.2可知，=e0.377=1.458，则VM==0.686。该系统的相位裕度为56°。