基于开环幅频曲线的性能指标及设计约束

在频域法校正中，针对最小相位系统，我们可以把控制系统的性能指标要求转化为期望的开环幅频特性，然后进行控制系统的串联综合校正（详见本书6.5节）。期望的开环幅频特性Gc（jω）G（jω）的幅值在低频段应有下限，以保证系统有满意的稳态误差；在高频段幅值应有上限，以抑制传感器噪声和系统中的未知高频动态干扰，从而保证系统具有鲁棒性。为了处理方便，从频率响应的思路出发，将低频处的下限和高频处的上限定义为关于频率的函数W1和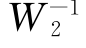，并在系统的开环幅频特性曲线上描述它们，如图6.10.1所示。

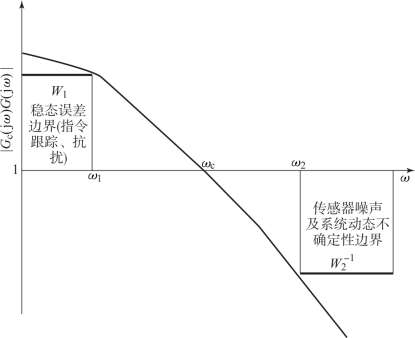
图6.10.1　基于开环幅频特性的性能指标描述

例如，若某控制系统要求以低于1%的误差跟踪0～ω1频率范围的任意正弦输入信号，那么在0≤ω≤ω1的频率区间内，W1应等于100。注意，实际系统的输入信号是比较复杂的，并不总是简单的阶跃、斜坡等信号，为了简化分析又不失准确性，可认为输入信号是由某些特定频率的正弦信号叠加合成的。(www.xing528.com)

一般控制系统的设计都是针对被控对象的标称数学模型G0（s）进行的，而实际系统由于温度变化、部件老化、环境变化等因素，被控系统的动态特性会偏离其标称情况，我们希望在系统动态特性发生变化时，控制系统依然可以稳定，即希望控制系统具有一定的鲁棒性。我们用W2（ω）描述不同频率处被控对象幅值变化的大小，即

式中G0（jω）为标称系统的频率特性。系统在低频段的建模精度一般比较高，因此W2在低频处通常很小，而在高频处W2会比较大，即系统存在未建模高频动态，因此我们希望ω2≤ω时，即在高频处使开环系统的幅值低于。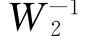

一般我们希望系统在尽可能宽的频率范围内保持小的系统误差，且系统在高频处具有鲁棒性，即希望W1和W2在各自的频率范围内尽可能大，并希望ω1尽可能接近ω2，这样就需要控制系统的开环幅频特性曲线以很陡的斜率快速地从W1降低到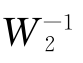。但是，根据伯德提出的幅相定理，斜率越陡，系统的相位裕度就会越小，甚至为负（在5.6.1节我们已经讨论了系统幅值与相位的近似关系）。所以，为保证系统具有一定的稳定裕度，在ω1和ω2这两个频率之间的频段上，系统的开环对数幅频特性应该以斜率-20 dB/dec的斜率穿越0 dB线，并在穿越频率ωc附近的约10倍频程内尽量保持这一斜率，这个限制条件是控制系统设计者必须遵守的约束条件。