扰动补偿复合校正方法优化

实际系统总是会受到干扰影响，如果干扰可测量，就可以设计补偿控制器消除干扰对系统输出的影响，这种设计原理就是20世纪40年代最早由苏联学者提出的不变性原理，按照消除的是干扰的稳态影响还是它的全部影响，分别称为稳态不变性或者完全不变性。不变性原理是一种非常重要、实用的控制系统设计思想。

下面将详细介绍按扰动补偿的复合控制的基本控制原理。

设按扰动补偿的复合控制系统如图6.9.1所示。图中，D（s）为可量测扰动，G1（s）和G2（s）为系统的前向通路传递函数，Gcf（s）为前馈补偿器的传递函数。扰动作用下的系统输出为

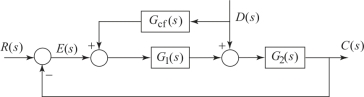
图6.9.1　按扰动补偿的复合控制系统

扰动作用下的系统误差为

若选择前馈补偿器的传递函数

则由式（6.9.1）和式（6.9.2）知，必有Cd（s）=0及Ed（s）=0。因此，式（6.9.3）称为对扰动的误差全补偿条件。

具体设计时，可以选择G1（s）的形式与参数，使系统获得满意的动态性能和稳态性能；然后按式（6.9.3）确定前馈补偿器的传递函数Gcf（s），使系统完全不受可量测扰动的影响。但是，误差全补偿条件式（6.9.3）在物理上往往无法准确实现，因为对由物理装置实现的G1（s）来说，其分母多项式次数总是大于或等于分子多项式的次数。因此，在实际应用中，多采用近似全补偿或稳态全补偿的方案。

按扰动补偿的复合控制的基本原理是，主要扰动引起的误差，由前馈控制进行全部或部分补偿：次要扰动引起的误差，由反馈控制予以抑制。这样，在不提高开环增益的情况下，各种扰动引起的误差均可得到补偿，从而有利于同时兼顾提高系统稳定性和减小系统稳态误差的要求。注意，由于前馈控制是一种开环控制，因此要求构成前馈补偿器的元部件具有较高的参数稳定性，否则将削弱补偿效果，并给系统输出造成新的误差。(www.xing528.com)

另外，从补偿原理来看，由于前馈补偿实际上是采用开环控制方式去补偿可量测的扰动信号，因此前馈补偿并不改变反馈控制系统的特性。

【例6.9.1】设按扰动补偿的复合校正随动系统如图6.9.2所示。图中K1/（T1s+1）为综合放大器和滤波器的传递函数，Km/[s（Tms+1）]为伺服电机的传递函数，D（s）为负载转矩扰动。试设计前馈补偿器Gcf（s），使系统输出不受扰动影响。

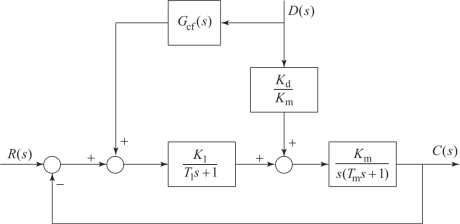
图6.9.2　带前馈补偿的随动系统

【解】由图6.9.2可见，扰动作用下的系统输出为

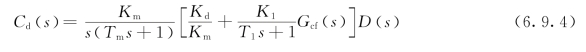
令

系统输出便可不受负载转矩扰动D（s）的影响。但是由于Gcf（s）的分子次数高于分母次数，不便于物理实现。若令

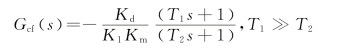
则Gcf（s）在物理上能够实现，且能达到近似全补偿目的，即在扰动信号作用的主要频段内进行了全补偿。此外，若取

则由式（6.9.4）可知，在稳态时，系统输出完全不受扰动的影响，这就是稳态全补偿，它在物理上更易于实现。