确定标准传递函数的最小节拍响应方法

控制系统的设计目标是：系统具有快速的阶跃响应，并且具有最小超调量。最小节拍（deadbeat）响应就是指以最小的超调量快速到达稳态响应的允许波动范围，并能够持续保持在该波动范围之内的响应，如图6.7.5所示。当系统输入为阶跃信号时，通常将允许波动范围定义为稳态响应的±2%误差带，即Δ=2%。具体地讲，最小节拍响应具有如下特征：

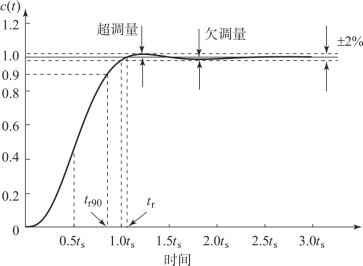
图6.7.5　最小节拍响应

①在阶跃输入作用下稳态误差为零；

②系统阶跃响应具有最小的上升时间和调节时间；

③0.1%≤阶跃响应超调量＜2%；

④阶跃响应欠超调＜2%。

其中，第③个和第④个特征意味着，一旦到达系统的调节时间，系统的响应就会进入并保持在±2%允许波动带内。

表6.7.3列出了具有最小节拍响应的二阶至六阶系统的标准化传递函数及阶跃响应的主要性能指标。在设计具有最小节拍响应特性的实际控制系统时，可以依据表6.7.3，根据系统的调节时间或上升时间等性能指标要求，确定所需要的ωn。然后选择合适的校正器类型，并令校正后的闭环传递函数等于期望的最小节拍响应标准传递函数，就可以最终确定所需要的校正网络。

表6.7.3　最小节拍响应系统的标准传递函数和性能指标

续表

(www.xing528.com)

【例6.7.2】考虑图6.7.6给出的单位反馈系统，受控对象为G（s）=，校正器为，设计具有最小节拍响应的系统。

图6.7.6　带前置滤波器的控制系统

【解】假设前置滤波器为

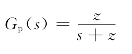
则校正后系统的闭环传递函数为

由表6.7.3可知，如果要求系统的调节时间为2 s（Δ=2%），则有ωnts=4.04，于是可以得到ωn=2.02，则具有最小节拍响应的系统的特征方程应为

比较系数后可以得到，具有最小节拍响应的系统参数有p=2.84，z=1.34，K=6.14。校正后系统的实际动态性能为σp%=1.65%，ts=2 s，tr=2.14 s，tr90=1.72 s。系统的单位阶跃响应曲线如图6.7.7所示。

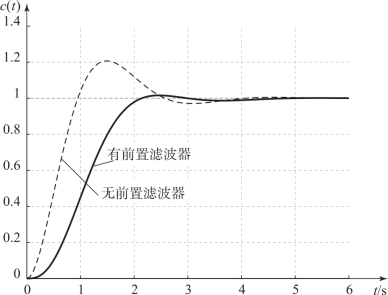
图6.7.7　例6.7.2系统的单位阶跃响应

当系统无前置滤波器时，系统的动态性能为σp%=21%，ts=3.48 s，tr=0.95 s，tr90=0.84 s。