基于齐格勒-尼柯尔斯法的PID控制器设计方案

对于被控对象比较复杂、数学模型难以建立的情况，在系统的设计和调试过程中，可以考虑借助实验方法，基于齐格勒-尼柯尔斯法（Ziegler and Nichols）对PID控制器进行设计。齐格勒-尼柯尔斯法又分为以下两种方法。

第一种方法：基于被控对象阶跃响应的整定法则

当被控对象的阶跃响应没有超调，且其响应曲线有如图6.6.9所示的S形状时，可以采用齐格勒-尼柯尔斯第一法整定PID控制器的参数。整定方法如下：

对单位阶跃响应曲线上斜率最大的拐点作切线，得参数L和T，则齐格勒-尼柯尔斯法整定PID控制器的参数如表6.6.1所示。

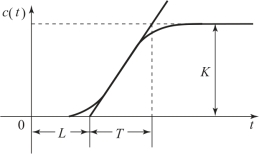
图6.6.9　S形响应曲线

表6.6.1　基于被控对象的阶跃响应整定PID控制器参数（第一法）(www.xing528.com)

第二种方法：基于系统等幅振荡响应的整定法

对于低增益时稳定而高增益时不稳定会产生振荡发散的系统，采用齐格勒-尼柯尔斯第二法（即连续振荡法）整定PID控制器参数。开始只加比例校正，系统先以低增益值工作，然后慢慢增加增益，直到闭环系统输出等幅度振荡为止。这表明被控对象加该增益时的比例控制系统已达稳定性极限，为临界稳定状态，此时测量并记录振荡周期Tu和比例增益值Ku，则齐格勒-尼柯尔斯法设定PID控制器的参数如表6.6.2所示。

表6.6.2　基于系统等幅振荡响应整定PID控制器的参数（第二法）

齐格勒-尼柯尔斯法参数整定法则只是给出了PID参数的一种合理估值，提供了进行精细调参的起点，而不是一次性给出了PID控制器参数的终值。通过整定法则得到的PID参数还需要在实际工程中反复调试，以获得满意的控制效果。