基于伯德图的PID控制器设计优化

1.比例-微分（PD）控制器的频率特性

PD控制器的传递函数为

当Kp=1时，图6.6.1给出了比例-微分控制器的伯德图。

图6.6.1　比例-微分控制器的伯德图

从图6.6.1中可以看出，在转折频率后，幅频曲线的斜率变为20 dB/dec，相位也变大，最大值接近90°，所以PD控制器可以改善系统的稳定程度。PD控制器的频域设计原则是合理放置PD的转折频率ω=，使得增加的相位发生在系统新的穿越频率附近，以提高系统的相位裕度。PD控制器能够增大系统的穿越频率，进而提高系统的闭环带宽，加快系统的响应速度。

从图6.6.1中还可以看出，幅值随着频率增大而继续增大，即PD控制器呈现高通特性，这是不希望的系统特性，因为实际系统会存在噪声，而且噪声通常为高频信号，PD控制器会放大其输入端的高频噪声。另外，纯微分环节在实际物理系统中也是不可实现的。

为了降低PD控制器的高频放大影响，通常在其分母上加一个一阶极点，如式（6.6.2）所示，其转折频率远高于PD控制器的转折频率，这样，既增加了系统的相位裕度，又限制了PD控制器对高频噪声的放大作用。

式（6.6.2）正是超前校正器的传递函数，因此，可以应用6.4.1节的超前校正设计方法在频域内进行PD控制器的设计。

2.比例-积分（PI）控制器的频率特性

PI控制器的传递函数为

还可以写为

其伯德图如图6.6.2所示。

图6.6.2　比例-积分控制器的伯德图

注意到，Gcj（ω）的幅值在频率ω较大时，是20lg Kp（dB），这意味着，如果Kp小于1，幅值将有衰减，这种衰减特性可以用来提高系统的稳定程度，即相位裕度。

在小于转折频率ω=1/Ti的频段上，PI控制器的幅频值随着频率的降低而增大，因而PI控制器能降低系统的稳态误差，但代价是系统相位滞后的增大，因此，必须把转折频率放在足够小的频率上，远离系统的穿越频率，以免降低系统的相位裕度。一般来说，PI控制器会降低系统的穿越频率和带宽。

在6.11.2节中，针对热钢锭机器人，给出了基于PI控制器的控制系统频域设计实例，可以看出其频域设计方法与滞后校正类似。

3.比例-微分-积分（PID）控制器的频率特性

PD控制器能够增加系统的相位裕度，提高系统稳定程度，但是对系统稳态误差并没有改进；PI控制器能同时提高系统的相对稳定程度（即增大相位裕度）和改善稳态误差，但是使系统响应速度变慢。当系统既需要在原穿越频率处增加相位裕度，又需要增大低频增益时，就须同时采用微分和积分控制。将式（6.6.1）和式（6.6.4）结合起来，就可得到PID控制器的传递函数，如式（6.6.5）所示，其伯德图如图6.6.3所示。

式（6.6.5）与PID控制器的惯常表达式Gc（s）=有点差别，但是这点差别无关紧要。PID控制器相当于将超前校正器和滞后校正器结合了起来，所以PID控制器有时也被称作超前-滞后控制器，它能同时改善系统的动态和稳态响应。

下面通过例6.6.1的航天器姿态控制系统，讲述一种基于伯德图的PID控制器设计方法。

图6.6.3　PID控制器的伯德图（Td/Ti=20）

【例6.6.1】航天器姿态控制系统的方框图如图6.6.4所示，系统存在干扰力矩和传感器动态。要求设计一个PID控制器，使得对阶跃干扰力矩的稳态误差为零，相位裕度为65°，并画出系统在阶跃输入作用下的系统响应曲线。(www.xing528.com)

图6.6.4　航天器姿态控制系统

【解】设计指标要求系统对阶跃干扰力矩的稳态误差为零，因此进入稳态时，被控对象的总输入力矩（Tc+DT）必须等于零，如果DT≠0，则有Tc=-DT，因此要想使误差为零，控制器Gc（s）中要包含积分环节，即控制器中须包含积分环节才会满足系统的稳态误差要求，用终值定理也可以证明Gc（s）中须包含积分环节。

无控制器时，系统的开环传递函数为：

G（s）的伯德图如图6.6.5中的虚线所示，幅频曲线的斜率是-40 dB/dec和-60 dB/dec，这说明如果没有微分控制，无论系统增益取何值，系统都会不稳定。因此为了使系统稳定，需要用微分环节将穿越频率附近的幅频曲线的斜率调整到-20dB/dec。下面我们来为系统设计一个PID控制器，PID控制器的表达式如下

该如何选择PID控制器的三个参数Kp、Td、Ti呢？最容易的切入点是：在合理的频率处获得65°的相位裕度，这可以通过调整Td参数来达到目的。注意，如果Ti比Td大很多，则Ti对相位裕度的影响很小。所以初始设计控制器时，可以暂不考虑积分控制，即先假设控制器的传递函数为Gc1（s）=Tds+1。

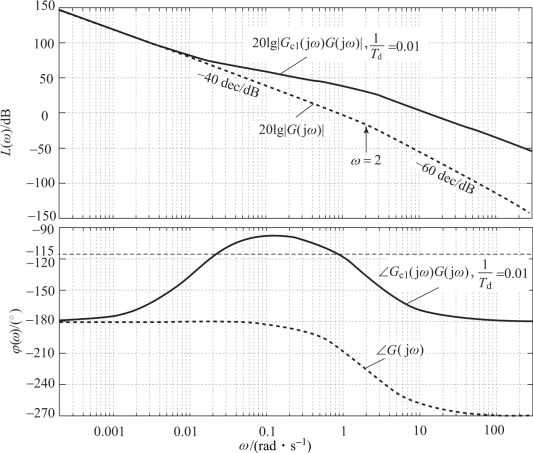
图6.6.5　Gc1（s）G（s）与G（s）的伯德图（Gc1（s）=100s+1）

我们首先观察一下图6.6.3中PID控制器的相位曲线，看看当Td变化时，校正系统Gc1（s）G（s）的频率特性会怎么变化。如果1/Td≥2 rad/s，则PID提供的超前角仅仅能抵消传感器的相位滞后，Gc1（s）G（s）的相位曲线还是不能向上穿越-180°，因此，相位裕度γ≤0，这是不可行的。如果1/Td≤0.01，则Gc1（s）G（s）的总相位在某些频率会接近-90°，并在一个较宽的频率范围上穿越-115°，因而能提供65°的相位裕度，如图6.6.5所示。

当1/Td=0.1时，Gc1（s）G（s）=（10s+1）G（s）的对数相频曲线如图6.6.6中的实线所示。1/Td=0.1是PD控制器能提供65°相位裕度的1/Td的最大值，若1/Td＞0.1，Gc1（s）G（s）的相位永远不会向上穿越-115°。当1/Td=0.1时，能产生65°相位裕度的频率是ωc=0.5 rad/s。

当1/Td=0.05时，系统相频特性如图6.6.6中虚线所示，表明1/Td=0.05能提供的最大穿越频率是ωc≈0.8 rad/s，因此0.05≤1/Td≤0.1是1/Td的合理选择区间，若1/Td的取值比0.05还小，虽然能增加系统的带宽，但是增加量非常有限；若1/Td比0.1大，则不会满足系统的相位裕度指标要求。1/Td是在合理区间内任选的，这里我们选择1/Td=0.1，此时系统对应的ωc=0.5 rad/s。

1/Ti的选择原则是要小于1/Td的，即1/Ti=0.005，若大于1/Td的时，可能会影响穿越频率处的相位，从而使系统的相位裕度减少。

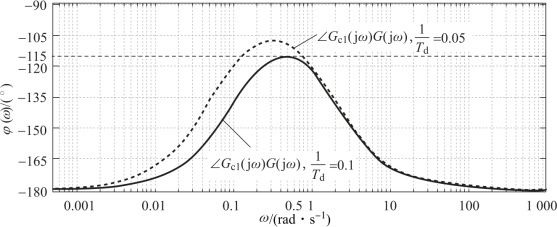
图6.6.6　Gc1（s）G（s）的对数相频曲线（Gc1（s）=Tds+1）

若选择1/Td=0.05，则可以获得更大的相位超前，系统的动态响应更快一些。

这时我们就确定了PID控制器的传递函数：

剩下的问题就是确定PID控制器的增益Kp，在前几节的串联校正中，我们选择开环增益以便满足系统稳态误差的要求，这里我们选择Kp是为了产生一个穿越频率，其对应的相位裕度为65°。当Kp=1时，绘制Gc（s）G（s）的伯德图如图6.6.7中的虚线所示，在ωc=0.5处，20lg=26 dB，因此令1/Kp=1026/20，则Kp=0.05，最终得到PID控制器为

已校正系统Gc（s）G（s）的伯德图如图6.6.7中实线所示，其相频曲线与Kp=1时相同。

图6.6.7　Gc（s）G（s）的伯德图（Kp=1和Kp=0.05）

需要注意的是，如果降低比例增益使得ωc≤0.02，系统的相位将小于-180°，系统将不稳定。

系统在阶跃输入下的时域响应如图6.6.8所示，由图可见，系统的阻尼特性比较好，这是因为系统的相位裕度是65°。

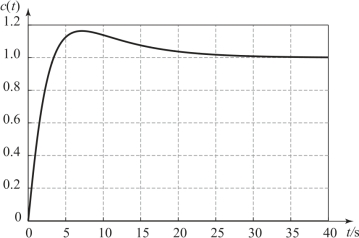
图6.6.8　航天器姿态控制系统的单位阶跃响应

注意，积分控制项确实使误差最终趋于零，但趋于零的速度很慢，这是由于把积分项1/Ti放在频率很低的地方，从而造成闭环传递函数存在着s=0.005附近的极点和零点。如果系统响应太慢而难以接受，可以增大1/Ti，但是这样会降低相位裕度和系统的阻尼程度。因此可以选择较小的1/Td，使得微分控制提供的相位裕度更大一些，这样即使1/Ti比较大，引起的相位滞后大一些，但仍然能够满足系统的相位裕度要求。

从上面的设计过程可以看到，系统的穿越频率（或带宽）是受到传感器动态特性的限制的。为了使系统响应速度快，必须要提高传感器的带宽；但另一方面，若传感器的带宽过大，可能会引入高频测量噪声，引起系统抖动。因此，设计者须在干扰引起的误差和传感器噪声引起的误差之间进行折中，看看那个指标对系统整体性能更重要。