基于期望开环频率特性的串联综合法校正方法优化

串联综合校正方法是将系统的性能指标要求转化为期望的开环对数幅频特性，再与待校正系统的开环对数幅频特性比较，从而确定校正器的形式和参数。由于只有最小相位系统的对数幅频特性和对数相频特性之间有确定的单值对应关系，故基于期望开环频率特性的串联综合法仅适合于最小相位系统的校正。

设原系统传递函数为G0（s），加入串联校正环节Gc（s）后系统满足指标要求，相应开环传递函数G（s）为期望开环传递函数，亦即

串联校正环节的对数幅频特性可以表示为

对于调节系统和随动系统，期望开环系统伯德图的一般形状如图6.5.1所示。由图可见，中频段的斜率为-20 dB/dec。

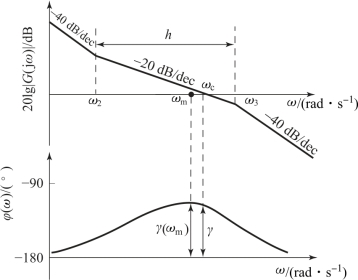
图6.5.1　期望的对数频率特性示意图（调节系统和随动系统）

相应的传递函数为

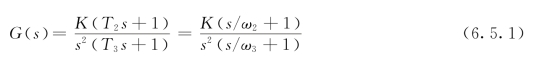
其相频特性表达式为

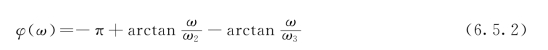
因而

γ（ω）表示开环相频特性对-180°的偏移，如图6.5.1所示。令=0，解出产生γ（ω）角的最大值γmax的对应频率ωm

ωm是转折频率ω2和ω3的几何中心点，其中ω2=1/T2，ω3=1/T3。

令h=ω3/ω2，h表示开环幅频特性20lg上斜率为-20 dB/dec的中频区宽度，则

将式（6.5.4）和h=ω3/ω2代入式（6.5.3），得γ（ω）角的最大值

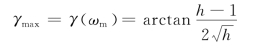
上式也可以写为

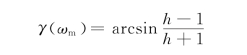
或者

一般情况下，ωm＜ωc，而且ωm与ωc比较接近，即ωm≈ωc，则γ（ωm）≈γ，γ为期望开环系统的相位裕度，因此式（6.5.6）可近似表示为

由于Mr≈，故有

式（6.5.8）和式（6.5.9）表明，中频宽度h与谐振峰值Mr一样，都是描述系统阻尼程度的频域指标，h越大，则Mr越小，系统的振荡程度越小。下面确定转折频率ω2、ω3与穿越频率ωc之间的关系。由图6.5.1可知

所以

由式（5.7.20）可知，当ω=ωr时，系统开环频率特性的幅值为

式（6.5.12）和式（6.5.13）就是ω2、ω3和ωc所要满足的最佳比例关系。在上面的设计过程中，我们把闭环系统的振荡指标Mr放在开环系统穿越频率ωc处，从而使期望对数幅频特性对应的闭环系统具有最小的Mr值。式（6.5.9）、式（6.5.12）和式（6.5.13）一起构成了设计期望开环对数幅频特性的重要公式，表明在给定谐振峰值Mr的情况下，一旦ωc确定，则转折频率ω2、ω3就可确定。

式（6.5.8）说明，当开环对数幅频特性中频宽度h给定时，按照式（6.5.8）计算出的谐振峰值Mr具有最小可能的值，也就是控制系统具有最小可能的Mr值，即控制系统具有最小的振荡性能指标；同样，式（6.5.9）说明，在给定谐振峰值Mr情况下，可以做到使中频段宽度h最小，也就是可使系统的开环对数幅频特性中频段内斜率为-20 dB/dec的长度最短，从而使控制系统易于实现。

为了确保系统具有以h表征的阻尼程度，通常选取

(www.xing528.com)

由式（6.5.8）知

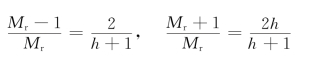
因此，参数ω2、ω3的表示也可以写成：

典型形式的期望开环对数幅频特性的求法如下：

（1）根据稳态性能指标要求，绘制低频段。首先，根据对系统型别ν的要求，确定低频段的斜率；其次，根据要求的稳态误差值，即静态误差系数或开环增益K，确定低频段的位置。

（2）根据系统的动态性能指标要求，绘制中频段。根据对系统响应速度及阻尼程度的要求，通过穿越频率ωc、相位裕度γ、中频段宽度h及中频段上下限频率ω3与ω2，绘制期望特性的中频段特性。为确保系统具有足够的相角裕量，取中频段幅频特性的斜率为-20dB/dec，这是控制系统设计的一个约束条件。ω2不宜太靠近穿越频率ωc，以保持所需的中频段宽度；但ω2也不宜过小，否则容易使系统响应出现“爬行”现象。

（3）根据系统的噪声抑制和抗高频干扰能力要求，绘制高频段。一般系统会存在高频未建模动态及测量噪声等高频干扰信号，因此希望高频段有较大的负斜率，以便衰减噪声、抑制干扰。原系统的高频段通常幅值很小且下降得很快，这对抑制高频噪声是有利的，若对系统的抗干扰性能没有特殊要求，则可以维持原系统高频段的形状不变，以简化校正器。

（4）从低频到中频，以及从中频到高频的连接段斜率变化不宜过大，一般变化斜率为±20 dB/dec。

【例6.5.1】已知某位置随动系统是一个单位反馈控制系统，该系统被控对象的传递函数为

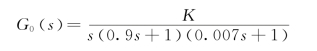
试基于期望开环频率特性法对该系统进行串联综合设计，使之具有下列性能指标：Kv≥500，σp%≤30%，ts≤0.25 s（Δ=5%）。

【解】首先将给定的时域指标化为频域指标，并绘制系统的期望开环对数幅频渐近曲线。由稳态指标确定期望开环对数幅频曲线的低频段。由稳态指标可知：系统应为Ⅰ型，即ν=1；其开环增益K=Kv≥500，取K=500。于是可确定系统的开环对数幅频曲线的低频渐近线为：斜率为-20dB/dec，当ω=1时，低频渐近线的延长线的高度为20lg K=20lg500 dB=53.98 dB。

由动态指标确定期望开环对数幅频曲线的中频段。根据超调量的要求，由式（5.7.17）及式（5.7.21）可得：

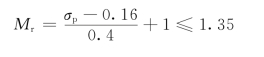
取Mr=1.3，则中频段的宽度为

为了适当地留有裕量，取

根据对调节时间的要求，由式（5.7.18）及式（5.7.21）可确定系统的期望穿越频率为：

取

于是可得中频段两端的转折频率为

由于对系统的抗噪声能力未提出特殊要求，为了简化校正器，维持原系统的高频段形状不变，根据以上变量数据，可绘制系统的期望开环对数幅频渐近曲线，如图6.5.2中实线Ⅰ所示，其中低频段与中频段衔接部分的斜率取为-40 dB/dec，于是在中频段与过ω2=7.33的横轴垂线的交点上，画一条斜率为-40dB/dec的直线，它与低频段渐近线相交点的对应频率，即为衔接部分的另一个转折频率ω1，由于

故

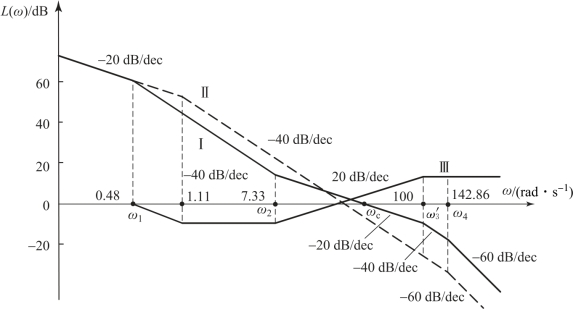
图6.5.2　例6.5.1系统的开环对数幅频图

此外，为了补偿受控系统在高频段的小时间常数T4=0.007对相位裕度的影响，将ω3修改成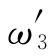，使得

即

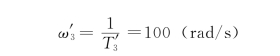
由图6.5.2中的曲线Ⅰ，可求得系统的期望开环传递函数为

由G0（s）可绘制原系统的开环对数幅频渐近曲线，如图6.5.2中虚线Ⅱ所示，它是按开环增益已调整至满足稳态指标要求来绘制的。将希望的开环幅频特性曲线Ⅰ与原系统的开环幅频特性曲线Ⅱ进行比较，即相减，则可求得校正器的对数幅频渐近曲线，如图6.5.2中的曲线Ⅲ所示，于是可确定校正器的传递函数为

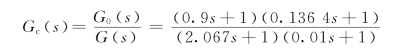
应用Matlab仿真，则可求得校正后系统的实际动态性能为σp%=27.4%，ts=0.21 s（Δ=5%），满足了系统的性能指标要求。