串联滞后超前校正技术优化方案

超前校正可以改善系统的稳定性和过渡过程，但适用范围有时受到限制；滞后校正可以提高系统的稳态精度和改善系统的稳定性，但缩小了系统的带宽，使系统反应迟钝。当待校正系统不稳定，且要求校正后系统的响应速度、相位裕度和稳态精度较高时，可以采用滞后-超前校正方式。其设计过程可以是：第一步用滞后校正使未校正系统对数幅频特性的中、高频段衰减，并取滞后校正后的穿越频率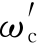略低于要求的穿越频率，但相位裕度小于设计指标；第二步，用超前校正进一步增加相位裕度，从而达到设计要求的指标，同时使穿越频率比略有提高。

【例6.4.4】若单位反馈系统的开环传递函数为

试设计一串联校正器，使其满足指标Kp=∞，Kv=40，ωc≥5.5 rad/s，γ≥40°。

【解】（1）未校正系统为Ⅰ型系统，故Kp=∞；根据要求K=Kv，可得K=40。

（2）绘制K=40时未校正系统的开环伯德图示于图6.4.8曲线①，由①查出ωc=11.1 rad/s，γ=-23.5°，系统不稳定。若采用一个超前校正器，则不可能满足γ=40°的指标；若采用滞后校正，在γ=40°时，ωc=3 rad/s，穿越频率太低，故采用超前-滞后校正试算。

（3）确定校正器滞后部分的传递函数。

由图6.4.8曲线①可以看出，若用滞后-超前网络的滞后部分将未校正系统中、高频段衰减15.6 dB，则=4.54 rad/s。这时穿越频率接近要求值，而相位裕度不足，再通过超前部分校正可能使相位裕度达到40°，并且穿越频率略有提高。

因此试选=4.54 rad/s，这时滞后部分的传递函数参数为

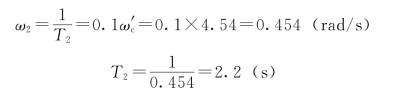
由于滞后部分把未校正系统的对数幅频特性中、高频段衰减15.6 dB，根据图6.3.9，则有

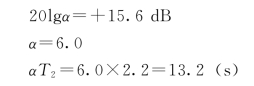
所以滞后部分的传递函数为

图6.4.8　串联滞后-超前校正

（a）幅频图；（b）相频图

（4）绘制滞后校正后的开环系统的伯德图示于图6.4.8曲线②，由曲线②查出=4.54 rad/s，γ′=18.7°。

（5）确定校正器中超前部分的传递函数。

由图6.4.8曲线②可以看出，经过滞后校正的对数幅频特性在ω=5 rad/s处斜率由-20 dB/dec变成-40dB/dec，这个频率也是未校正系统的转折频率。若将超前部分的第一个转折频率选为ω1=1/T1=5 rad/s，则-20dB/dec斜率的直线将延长，并使其一直通过0dB线。这样相位裕度也将增加，故选取ω1=5 rad/s，即T1=1/5=0.2 s。超前校正部分的第二个转折频率为=5×6.0=30 rad/s。而(www.xing528.com)

所以，超前校正部分的传递函数为

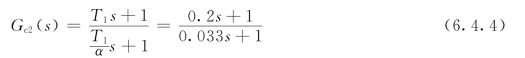
（6）确定滞后-超前校正器的传递函数。

由式（6.4.3）和式（6.4.4）得滞后-超前校正器的传递函数为

（7）绘制滞后-超前校正之后的系统开环伯德图。

校正后的系统开环传递函数为

根据上式绘出校正后的开环系统伯德图示于图6.4.8曲线③，由曲线③查出γ″=45.8°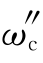，=5.71 rad/s，满足设计要求。

图6.4.9给出了滞后校正后系统（实线）、滞后-超前校正后系统（虚线）的单位阶跃响应曲线。

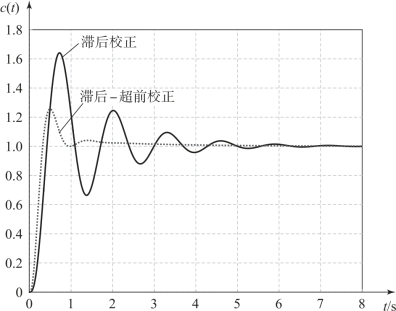
图6.4.9　滞后校正后系统、滞后-超前校正后系统的阶跃响应曲线

从上例归纳出设计滞后-超前校正器的步骤如下：

（1）根据稳态精度的要求，确定系统开环增益K。

（2）绘制上述K值时的未校正系统伯德图，查出ωc、γ、Kg的数值。

（3）根据要求的相位裕度，考虑校正器的超前部分所增加的相位角，选择滞后校正的穿越频率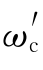和相位裕度γ′，然后按照滞后校正的方法确定校正器中的滞后校正部分的传递函数。

（4）取未校正系统对数幅频特性0 dB附近斜率由-20 dB/dec变至-40 dB/dec的转折点为超前校正的对数幅频特性的第一个转折频率ω1=1/T1，第二个转折频率为ω2=α/T1，最后得超前校正器的传递函数。

（5）绘制滞后-超前校正后的开环系统的伯德图，并校验系统指标。若不满足，则重复上述过程。