超前校正器的作用与应用

图6.3.1（a）给出了用无源电路网络实现的超前校正器，该无源电路网络的传递函数为

图6.3.1　无源超前网络及零极点图

（a）无源超前网络；（b）零极点分布图

式中

由式（6.3.1）可见，采用无源超前校正网络进行校正时，整个系统开环增益会降低α倍，这可以提高放大器的增益来补偿。

注意，这里的“超前校正器”以前常被人们称作“超前校正网络”，因为早期控制系统的超前校正大多是采用无源或者有源的超前电路网络实现的。考虑到近年来控制算法已大多由微处理器实现，而且国外的很多优秀教材都将其称为“lead compensator”，因此本书将“超前校正网络”改称为“超前校正器”。同理，本书将“滞后校正网络”改称为“滞后校正器”，将“滞后-超前校正网络”改称为“滞后-超前校正器”。

超前校正器的传递函数为

其零极点分布图如图6.3.1（b）所示。超前校正器的对数频率特性为

超前校正器Gc（s）的伯德图如图6.3.2所示。

由图6.3.2可以看出，超前校正器是高通滤波器，它对于频率在1/（αT）和1/T之间的正弦信号有明显的微分作用，在此频率范围内，输出信号相位角比输入信号相位角超前，超前校正器的名称由此而得，我们就是利用超前校正器提供的超前角来改善系统特性的。由图6.3.2还可以看出，超前校正器的相位有一个极大值φmax，对式（6.3.4）两端对ω求导并令其等于零，可得极大值频率为

将式（6.3.5）代入式（6.3.4），得最大超前角为

或(www.xing528.com)

上式表明，φmax仅与α值有关。α值越大，则超前校正器的超前作用越强（即φmax越大），但同时，超前校正器的微分效应越强，为了保持较高的系统信噪比，实际选用的α值一般不超过20，超前校正器提供的φmax不会超过70°。

L（ω）的转折频率分别为

图6.3.2　超前校正器的伯德图

其几何中心为

比较式（6.3.7）和式（6.3.5）可知，出现最大超前角的频率为两转折频率ω1和ω2的几何中点。当ω=ωm时，超前校正器对数幅频值为

将式（6.3.5）代入上式可得

图6.3.2中的对数幅频曲线为超前校正器对数幅频曲线的渐近线形式，当α=10时，超前校正器的真实对数幅频曲线如图6.3.3中的粗实线所示。

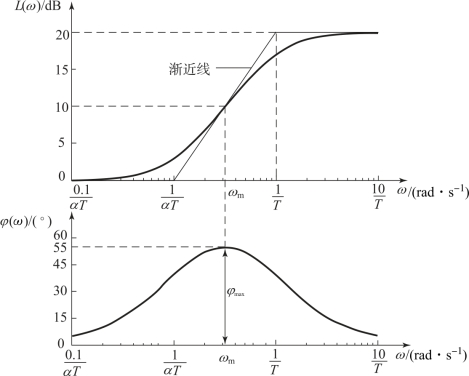
图6.3.3　超前校正器的伯德图与渐近线（α=10）

不同α下超前校正器的伯德图如图6.3.4所示。

图6.3.4　不同α情况下超前校正器的伯德图