磁盘驱动器读取系统的相关知识

图1.7.7所示的磁盘驱动器是用弹性簧片来悬挂磁头的，当考虑簧片的弹性影响时，磁头位置控制系统如图5.8.4所示。磁头与簧片的典型参数为ζ=0.3，ωn=18.85×103rad/s。当K=400时绘制开环系统的对数幅频曲线的渐近线图，并确定磁盘驱动读取系统的幅值裕度Kg（d B）、相位裕度γ及闭环系统的带宽频率ωb，估算系统单位阶跃响应的σp%和ts。

图5.8.4　磁头位置控制系统（包括簧片的弹性影响）

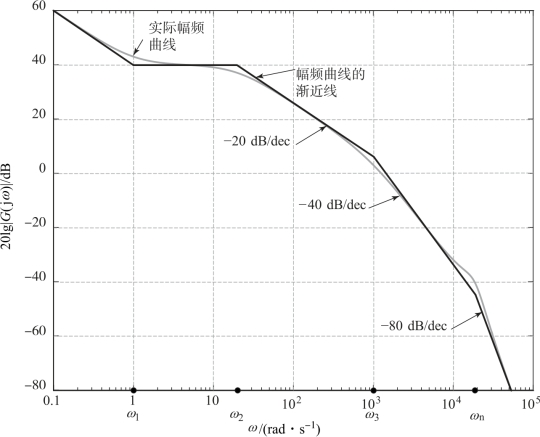
【解】取K=400，当ω=0.1时，20lg=60 dB，据此确定了低频段上的一点，然后根据各典型环节的转折频率，绘制开环对数幅频曲线的渐近线如图5.8.5所示。

基于Matlab画出的开环系统的伯德图如图5.8.6所示，可知：Kg=22.9 dB，γ=37.2°，ωc=1 250 rad/s。

绘制磁盘驱动读取系统的闭环对数幅频曲线如图5.8.7所示，可知ωb=2 000 rad/s。20lg Mr=3.9，Mr=1.56。由于簧片自然振荡频率ωn位于闭环带宽ωb之外，所以簧片弹性对系统动态性能的影响甚微，原系统可降阶为二阶系统。

如果按照典型二阶系统的γ-ζ曲线（图5.7.7），可知ζ≈0.35，也可以根据图5.7.3 Mr与ζ的关系确定阻尼的值。根据式（5.7.5），可得ωn≈1 395，因此估计得到闭环系统的调节时间（Δ=2%）为

(www.xing528.com)

图5.8.5　图5.8.4所示系统的对数幅频曲线

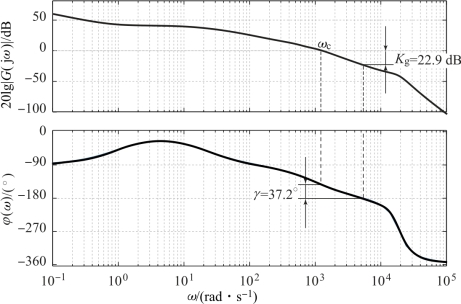
图5.8.6　图5.8.4所示系统的开环伯德图

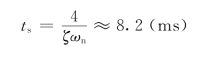
由σp%=×100%，可计算得到超调量σp%≈30.9%。而实际系统单位阶跃响应的时域指标为σp%=31.4%，ts=9.8 ms（Δ=2%），可见估算的时域指标跟实际系统的性能比较接近。经分析可知，原系统的确可以近似为如下二阶系统：

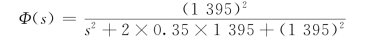
图5.8.7　闭环系统的幅频曲线