雕刻机控制系统的优化

某雕刻机利用电机来驱动雕刻针运动，使之到达指定的位置。图5.8.1给出了雕刻机x方向位置控制系统的框图。

图5.8.1　雕刻机x方向位置控制系统框图

本例的设计目标是：用频域法设计增益K的值，使系统阶跃响应的各项指标保持在允许范围内。

【解】本例设计的基本思路是：首先选择增益K的初始值，绘制系统的开环和闭环对数频率特性曲线，然后用闭环对数频率特性来估算系统时间响应的各项指标；若系统性能不满足设计要求，则调整K的取值，再重复前面的设计过程；最后，对实际系统进行仿真来检验设计结果。

先取K=2，开环系统伯德图如图5.8.2所示，系统的相位裕度γ=32.6°，ωc=0.75 rad/s，Kg=9.5dB，相应的闭环系统是稳定的。

图5.8.2　雕刻机开环系统的伯德图

在闭环传递函数

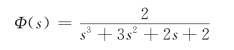
中令s=jω，可得闭环频率特性函数为

(www.xing528.com)

由此可画出闭环对数幅频图如图5.8.3所示。从图5.8.3中可以看出，当ωr=0.82时，对数幅值增益达到最大，因此有

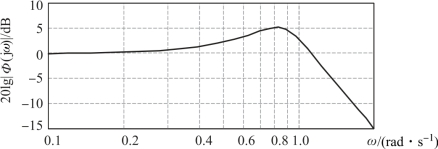
图5.8.3　闭环系统的对数幅频图

根据图5.8.3，可认为系统的主导极点为共轭复数极点，再根据图5.7.3给出的关系曲线或根据式（5.7.6），可以得到Mr=1.836对应的阻尼系数ζ=0.28。

因为ωr=ωn=0.82，则无阻尼自然振荡频率

于是，雕刻机控制系统的二阶近似模型应为

根据该近似模型，估计得到的系统超调量为39.8%，调节时间（Δ=2%）为

再按实际三阶系统进行仿真，得到的实际系统的超调量为39%，调节时间为16 s。结果表明，式（5.8.1）是一个合理的二阶近似模型，在控制系统的分析和设计工作中，可以用它来调整系统的控制器参数。在本例中，如果要求更小的超调量，应取K＜2，然后重复上面的设计过程。