开环系统频域指标与闭环系统时域指标的关系分析

1.开环对数频率特性与静态误差系统的关系

对数幅频特性低频段的渐近线的斜率决定了系统的类型及无静差度，即：

低频段渐近线为水平线，则系统为零型系统，有静差，静态位置误差系数Kp=K；

低频段渐近线斜率为-20dB/dec，则系统为Ⅰ型系统，一阶无静差，静态速度误差系数Kv=K；

低频段渐近线斜率为-40dB/dec，则系统为Ⅱ型系统，二阶无静差，静态加速度误差系数Ka=K。

其中K是系统的开环增益。低频渐近线或其延长线在ω=1的对数幅频值为20lg K。因此，从伯德图低频段上可以一目了然地看出系统的类型及相应的误差品质。

【例5.7.2】已知开环系统的对数幅频特性如图5.7.6所示。分别确定每种情况下的静态误差系数与ω1、ω2与ω3之间的关系。

由图5.7.6可以看出，对数幅频特性0、Ⅰ和Ⅱ分别对应于零型系统、Ⅰ型系统和Ⅱ型系统。

对于零型系统有

图5.7.6　例5.7.2的伯德图

从而求得

对于Ⅰ型系统有

从而求得

对于Ⅱ型系统有

得

分析上面关于Kp、Kv和Ka的表达式可见：若ωc大，ω2大，ω1小，则静态误差系数就大，相应的稳态误差就小。

2.二阶系统开环频域指标与超调量、响应速度的关系

系统时域指标物理意义明确、直观，但不能直接应用于频域的分析和综合。闭环系统频域指标ωb虽然能反映系统的跟踪速度和抗干扰能力，但由于需要通过闭环频率特性加以确定，在校正元件的形式和参数尚需确定时显得较为不便。而系统开环频域指标相位裕度γ和穿越频率ωc可以直接利用开环对数频率特性确定，且γ和ωc的大小在很大程度上决定了闭环系统的性能，因此工程上常用γ和ωc来估算系统的时域性能指标。

因为典型二阶系统的开环频率特性为(www.xing528.com)

根据ωc定义有

解上面方程，得

典型二阶系统的开环相频特性为

则其相位裕度为

式（5.7.15）便是阻尼系数ζ与相位裕度γ之间的关系式，它将系统的频域响应与时域响应联系了起来，对应的γ-ζ曲线如图5.7.7中的实线所示。为使控制系统具有良好的动态特性，一般希望30°≤γ≤70°，在这个范围内，可以得到γ与ζ之间的线性近似关系为

γ的单位为度（°）。当ζ≤0.7时，式（5.7.16）具有很高的近似精度，且简单实用，在频域响应与时域瞬态响应之间很直观地建立了联系。式（5.7.16）是二阶系统的近似关系式，也同样适用于具有一对欠阻尼共轭主导极点的高阶系统。

图5.7.7　典型二阶系统的γ-ζ曲线

【例5.7.3】设一单位反馈系统的开环传递函数为

若已知单位速度信号输入下的稳态误差ess=，相位裕度γ=60°，试确定系统时域指标σp%和ts。

【解】因为该系统为Ⅰ型系统，单位速度输入下的稳态误差为，由题设条件得K=9。由γ=60°，查图5.7.7得阻尼ζ=0.62，因此超调量

3.高阶开环系统频域指标与超调量、响应速度的关系

对于高阶系统，开环频域指标和时域指标不存在解析关系式。通过对大量系统的γ和ωc的研究，归纳为下述两个近似估算公式

其中

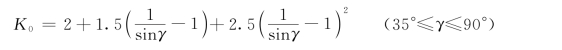
应用上述经验公式估算高阶系统的时域指标，一般偏于保守，即实际性能比估算结果要好。控制系统进行初步设计时，使用经验公式，可以保证系统达到性能指标的要求且留有一定的余地。