1.谐振峰值与超调量的关系
由式(5.7.6)可以画出Mr与阻尼ζ的关系曲线,如图5.7.3所示,可见阻尼系数越小,Mr越大。因为阻尼系数与超调量σp%相关,所以可进一步画出σp%与Mr的关系曲线,如图5.7.4所示。σp%随Mr的变化规律有明显的物理意义:当闭环幅频特性有谐振峰值时,系统对信号有选择性,它使得信号频谱中在ω=ωr附近的分量通过系统后显著增强。因此,当Mr较大时,系统的单位阶跃响应表现出频率接近ωr(实际是![]() )的强烈振荡。一般设计控制系统时,希望Mr<1.5。
)的强烈振荡。一般设计控制系统时,希望Mr<1.5。

图5.7.3 Mr与ζ的关系曲线

图5.7.4 以ζ为参变量时σp%随Mr的变化曲线
从式(5.7.7)可以看出,ωr与自然振荡频率ωn不相等,但是当ζ比较小时,如ζ<0.4,ωr≈ωn,我们可以认为在自然振荡频率处产生了谐振峰值。另外需要注意,当ζ>0.707时,将不会有谐振峰值,但在0<ζ<1的区间内,系统都有超调量。
2.带宽与时域响应速度的关系
因为调节时间
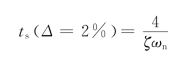
 (https://www.xing528.com)
(https://www.xing528.com)
图5.7.5给出了被调节时间、峰值时间、上升时间规范化后的带宽ωbts、ωbtp、ωbtr与阻尼系数ζ的关系曲线。

图5.7.5 规范化带宽与阻尼系数ζ的关系
(a)ωbts与ζ的关系;(b)ωbtp与ζ的关系

图5.7.5 规范化带宽与阻尼系数ζ的关系(续)
(c)ωbtr与ζ的关系
在不改变阻尼系数条件下,增加带宽ωb会提高系统的响应速度,tr、tp、ts均会减小。这一结论的物理意义是,当增加带宽频率时,系统的惯性减小了,更容易使单位阶跃信号中的高频分量通过,因此系统的响应速度得以提高。
【例5.7.1】若要求闭环系统的超调量是20%,调节时间是2 s,求系统的带宽。
【解】由σp%=![]() ×100%,可以解出阻尼比ζ=0.456。
×100%,可以解出阻尼比ζ=0.456。
利用式(5.7.8),可以得到ωb=5.79 rad/s。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




