系统闭环的频域指标分析

1.带宽

反馈控制系统的闭环传递函数为

作用在控制系统的信号除了有用输入信号，还有扰动和随机噪声，闭环系统的频域性能指标应该能反映控制系统跟踪控制输入信号和抑制干扰信号的能力。

Φ（jω）为系统闭环频率特性，当闭环幅频增益下降到其频率为零时的分贝值以下3（dB），即0.707Φ（j0）时，对应的频率称为带宽频率，记为ωb。即当ω＞ωb时，有

而频率范围（0，ωb）称为系统的带宽，如图5.7.1所示。

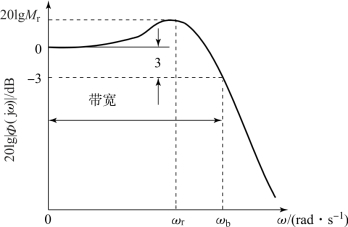
图5.7.1　二阶闭环系统的幅频图

带宽定义表明，对高于带宽频率ωb的正弦输入信号，系统输出将呈现较大的衰减。对于Ⅰ型和Ⅰ型以上的开环系统，由于=0，故

带宽是频域中一项非常重要的性能指标。对于一阶和二阶系统，带宽与系统参数具有解析关系。

设一阶系统的闭环传递函数为

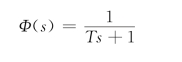
因为Φ（j0）=1，按带宽定义

可求得带宽频率

由式（5.7.2）可知，一阶系统的带宽和时间常数T成反比，带宽越大，系统的响应速度越快。

对于二阶系统，闭环传递函数为

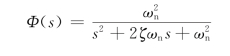(www.xing528.com)

系统幅频特性为

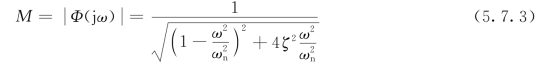
如图5.7.1所示。

因为=1，由带宽定义得

则

根据式（5.7.4）绘出ωb/ωn随阻尼ζ的变化曲线如图5.7.2所示。由图5.7.2可见，ωb为ζ的减函数。系统带宽ωb与自然振荡频率ωn之间存在着如下线性近似关系：

当0.3≤ζ≤0.8时，

当ζ=0.707时，ωb=ωn。

图5.7.2　二阶系统标准化带宽（ωb/ωn）与阻尼系数ζ的关系

由式（5.7.4）知，二阶系统的带宽和自然振荡频率ωn成正比。带宽越大，系统复现输入信号的能力越强，但另一方面，带宽越大，系统抑制输入端高频干扰的能力越弱，因此系统带宽的选择在设计中应折中考虑，不能一味求大，否则会加大设计难度，增加系统部件成本，降低系统实际运行时的可靠性，甚至导致系统失稳。

2.谐振峰值和谐振频率

对式（5.7.3）的二阶系统闭环幅频特性求关于ω2的导数，并令其导数为0，可以得到最大的幅频值，即谐振峰值Mr：

对应的频率称为谐振频率ωr，

由式（5.7.6）可知，谐振峰值表征了系统的阻尼程度。大的谐振峰值一般表示系统存在一对具有较小阻尼系数的闭环主导极点，从而使系统产生不希望的动态响应。

注意，只有ζ＜0.707时，ωr才是实数。因此当ζ＞0.707时，闭环系统是不会产生谐振现象的。