非最小相位系统的稳定性分析

必须指出，5.6.1节关于最小相位系统的稳定裕度结论不能照搬到非最小相位系统，应从奈氏判据出发，恰当地应用相位裕度和增益裕度的概念，才能正确地分析非最小相位系统的稳定裕度。例如对于具有不稳定开环极点的非最小相位系统，开环奈氏图曲线需要包围临界点（-1，j0），也就是奈氏曲线与负实轴的交点需要在（-1，j0）左侧，系统可能才会稳定，否则系统可能不稳定，因此系统的增益裕度是负的，系统才可能稳定。

例如，针对开环传函G（s）=，该系统稳定时将具有负的增益裕度和正相位裕度，奈氏曲线与负虚轴的穿越点离（-1，j0）的距离依然表明了系统的相对稳定程度，其增益裕度和正相位裕度的定义如图5.6.8所示。

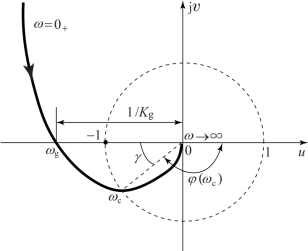
图5.6.8　G（s）=的稳定裕度定义示意图

当K=1时，G（s）=的幅值裕度是-6.02 dB，相位裕度为45.8°，ωc=1.82 rad/s，系统是稳定的。K=时，系统临界稳定。当0＜K＜时，系统不稳定。

对于非最小相位系统，稳定裕度的正确解释需要进行仔细的研究。确定非最小相位系统的稳定程度最好采用奈氏图。

【例5.6.2】某单位反馈控制系统的开环传递函数为(www.xing528.com)

当K=9时，求使系统稳定的延迟时间τ的范围。

【解】G（s）=的穿越频率ωc=2.8 rad/s，相位裕度γ=38.9°。

系统的延时环节不会改变幅频特性曲线，但是会导致相位的滞后，为了保证系统稳定，能够容许的最大时延满足γ=57.3ωcτ，即

求解得到τ=0.24 s，也就是说，如果延时常数小于0.24 s，则闭环系统可以保持稳定。