如何判断非最小相位系统的稳定性

在运用奈奎斯特稳定判据对非最小相位系统进行稳定性分析时，要特别注意系统开环幅相曲线的绘制，尤其是当非最小相位系统中还存在着积分环节时的情况。

【例5.5.5】系统开环传递函数为

试用奈氏判据判别闭环系统的稳定性。

【解】当ω=0+时，∠G（jω）H（jω）=-270°；ω=∞时，∠G（jω）H（jω）=-90°

由于开环传递函数中存在一个积分环节，所以需要从ω=0+的地方逆时针补画四分之一个半径为无穷大的圆弧，补画至G1（s）H1（s）=的幅相曲线的起点处。当ω=0时，∠G1（jω）H1（jω）=-180°。画出开环系统的幅相频率特性曲线如图5.5.15所示。下面求幅相曲线与负实轴的交点。

G（jω）H（jω）的幅相曲线与实轴交点处虚部为零，因此在这一点有

图5.5.15　G（s）H（s）=K1（K2s+1）/[s（s-1）]的奈氏图

即ω2=1/K2。交点处G（jω）H（jω）的实部为(www.xing528.com)

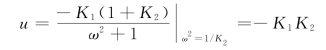
当-K1K2＜-1，即K1K2＞1时，奈氏曲线包围（-1，j0）点的圈数N=1-，则闭环系统在右半s平面的极点数为

因此，当K1K2＞1时系统稳定。

【例5.5.6】若系统的开环传递函数为

试用奈氏判据判别在τ=0 s和τ=1 s两种情况下的闭环稳定性。

【解】当τ=0 s时，系统为无延时环节情况；当τ=1 s时，系统为有延时环节情况。图5.5.16绘出了上述两种情况的对数频率特性曲线。

由图5.5.16可以看出，两种情况的对数幅频特性相同；而对数相频特性不同，曲线①对应τ=0 s，曲线②对应τ=1 s情况。对于τ=0 s情况，正负穿越数之差N=0，又由开环传递函数知P=0，根据奈氏判据则有，Z=P-2N=0-0=0，所以，闭环系统稳定；对于τ=1 s时的情况，正负穿越数之差N=-1，而P=0，根据奈氏判据有Z=P-2N=0-2×（-1）=2，所以闭环系统不稳定。

由此例可知，延时环节对于系统幅频无影响，而使相频随ω增加而滞后增加，因此延时环节使系统稳定性变坏。但是如果延时时间τ比系统惯性环节时间常数小得多，在开环对数幅频曲线通过0dB处所引起的相位滞后不大，则对系统稳定性的影响也不大。

图5.5.16　例5.5.6系统的伯德图

（a）幅频图；（b）相频图