稳定性判据：对数频率

使用对数频率特性的奈氏判据称为对数频率稳定性判据，或仍称为奈氏判据。为此先介绍一下穿越的概念。

1.穿越的概念

开环系统幅相曲线G（jω）H（jω）通过（-1，j0）点以左的负实轴称为穿越。沿ω增加的方向，G（jω）H（jω）曲线自上向下通过（1，j0）点之左的负实轴称为正穿越，它意味着ω增加时，G（jω）H（jω）幅相频率特性的辐角增加；反之，沿ω增加的方向，G（jω）H（jω）幅相曲线自下向上通过（-1，j0）点以左的负实轴称为负穿越，它意味着ω增加时，G（jω）H（jω）的幅角减小。G（jω）H（jω）曲线自上向下止于或自上向下起于（-1，j0）点左侧的负实轴，则称为半次正穿越；同理，G（jω）H（jω）自下向上止于或自下向上起于（-1，j0）点左侧的负实轴，则称为半次负穿越。如图5.5.12所示的幅相频率特性，2点为负穿越一次，4点为正穿越一次，5点在（-1，j0）点之右不算穿越。

正穿越一次对应G（jω）H（jω）曲线逆时针包围（-1，j0）点一周，负穿越一次对应G（jω）H（jω）曲线顺时针包围（-1，j0）点一周。因此，开环系统幅相曲线包围（-1，j0）点的圈数可表示为

图5.5.12　穿越示意图

N=（正穿越次数）-（负穿越次数）

2.对数频率稳定性判据

图5.5.13（a）、（b）分别示出某系统的幅相曲线（奈氏图）和伯德图。从图5.5.13可以看出两者之间存在下述关系：

（1）幅相曲线图上以原点为圆心的单位圆对应对数幅频伯德图上的零分贝线，如图5.5.13（a）中的3点在单位圆上，在图5.5.13（b）的3点在零分贝线上；在[GH]平面单位圆之外的幅相曲线对应对数幅频曲线L（ω）＞0部分；在[GH]平面单位圆之内的幅相曲线对应对数幅频曲线L（ω）＜0部分。

图5.5.13　某系统的奈氏图和伯德图

（a）奈氏图；（b）伯德图

（2）幅相频率特性图的负实轴在对数相频图上对应-180°线，如图5.5.13（a）、（b）中的1、2、4三点属于这种情况。(www.xing528.com)

这样，G（jω）H（jω）幅相曲线的穿越数可根据在L（ω）＞0的区间内，φ（ω）曲线与-180°线的交点来计算，即在L（ω）的正值区间，φ（ω）曲线自下向上通过-180°线为正穿越（对应沿ω增加方向辐角增加），φ（ω）曲线自下向上止于或自下向上起于-180°线时，则称为半次正穿越；φ（ω）曲线自上向下通过-180°线为负穿越（对应沿ω增加方向辐角减小），φ（ω）曲线自上向下止于或自上向下起于-180°线，则称为半次负穿越。

根据上述关系，对数频率稳定性判据叙述如下：若在对数幅频的正值区间，对数相频曲线φ（ω）对-180°线的正穿越数与负穿越数之差为N，而开环系统特征方程在右半s平面的根数为P，则闭环系统在右半s平面的根数为Z=P-2N，当Z=0时，闭环系统是稳定的。

当G（s）H（s）包含积分环节时，需从ω=0+开环幅相曲线的对应点G（j0+）H（j0+）起，逆时针补作ν×90°、半径为无穷大的虚圆弧，对应地，需在对数相频曲线ω较小且L（ω）＞0的点处向上补作ν×90°的虚直线。

【例5.5.4】若系统的开环传递函数为

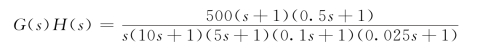
试用奈氏判据判别其闭环系统的稳定性。

【解】系统的伯德图示于图5.5.14，在相频曲线左端向上补画ν×90°的直线至0°相位线。

由图5.5.14可知，在ω＜5 rad/s区间，L（ω）＞0 dB，而φ（ω）曲线在ω=0.18 rad/s处自上而下通过-180°线，负穿越一次，在ω=1.3 rad/s处自下而上通过-180°线，正穿越一次，故N=1-1=0；又由开环传递函数知道P=0。根据奈氏判据有

所以，闭环系统稳定。

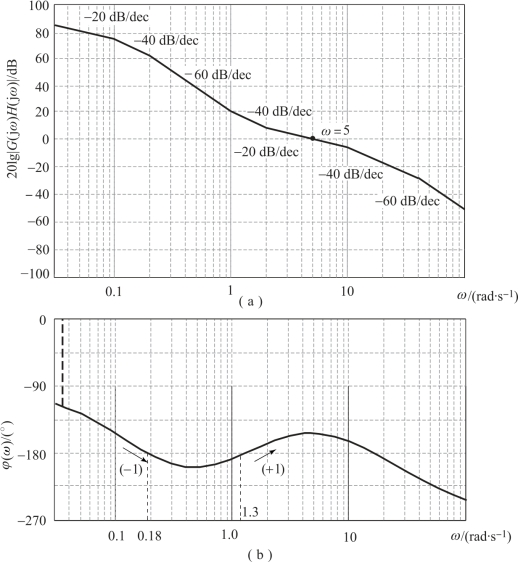
图5.5.14　例5.5.4系统的伯德图

（a）幅频图；（b）相频图