开环系统的奈氏判据在含有积分环节时的推广

1.Cs选取

辐角原理的使用条件是在路径Cs上无F（s）的极点和零点，这就要求在图5.5.5所示的路径Cs上无开环传递函数G（s）H（s）的极点。但是当开环传递函数中含有积分环节时，这个条件遭到破坏。为了解决这个问题，做如下处理，令Cs在坐标原点附近所走的路径取半径为无穷小的半圆，使其绕过坐标原点，而其他地方不变。处理后的路径Cs如图5.5.8所示，这时的Cs可用下面四段描述。

（1）动点s沿负虚轴移动时，s=jω，ω从-∞→0-变化。

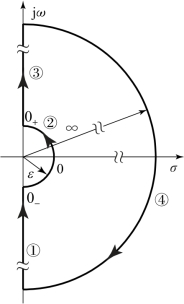
图5.5.8　当开环传递函数中含有积分环节时Cs路径

（2）动点s沿无穷小半圆移动时，s=θ从-90°→0°→+90°变化。其中，θ=-90°对应ω=0-，θ=0°对应ω=0，θ=+90°对应ω=0+。

（3）动点s沿正虚轴移动时，s=jω，ω从0+→∞变化。

（4）动点s沿无穷大半圆移动时，s=R ejθ，R→∞，θ从+90°→0°→-90°变化。

如上处理，实质上是将G（s）H（s）在坐标原点的极点画到了左半s平面，而其他极点保持不变。这时路径Cs上不再含有G（s）H（s）的极点，因此奈氏判据可重新应用了。但应该指出的是，CF曲线和系统开环幅相曲线的画法也应做相应的改变。

2.开环系统幅相曲线的画法

当开环系统含有积分环节时，其传递函数可表示为

（1）当s沿图5.5.8所示Cs的路径①、③、④移动时，G（s）H（s）幅相曲线的画法与5.3.2节相同，即为系统的开环幅相曲线。

（2）当s沿图5.5.8所示Cs的路径②移动时，有

由式（5.5.11）可知，当s沿图5.5.8的无穷小半圆移动时，，所以→∞；而θ从-90°→0°→+90°变化，所以∠[G（s）H（s）]由ν×90°→0°→-ν×90°变化或Δ∠[G（s）H（s）]=-ν×180°，即当s沿无穷小半圆逆时针移动时，G（s）H（s）沿无穷大半径的圆弧顺时针移动ν×180°。

若Cs取图5.5.8的上半部，则无穷小半圆只取横轴以上四分之一圆弧。当s沿上四分之一无穷小圆弧逆时针移动时，即当ω由0→0+变化时，G（s）H（s）曲线沿无穷大半径圆弧顺时针移动ν×90°。

综上所述，可归纳出含有积分环节时的幅相曲线的画法为：第一步，画出除ω由0→0+以外的幅相曲线，这就是不考虑s取无穷小半圆时的情况。其起点对应ω=0+；第二步，从G（j0+）H（j0+）开始，以R→∞为半径顺时针补画ν×90°圆弧，此时对应的ω是由0→0+。这两部分衔接起来，则得含有积分环节时的幅相曲线。图5.5.9（a）、（b）、（c）分别示出ν=1、2、3时的幅相曲线，图中虚线对应s取半径为无穷小四分之一圆弧时的G（jω）H（jω）曲线。

图5.5.9　ν=1、2、3时的开环奈氏曲线(www.xing528.com)

（a）ν=1；（b）ν=2；（c）ν=3

同理，当开环系统含有等幅振荡环节，即

即开环系统在虚轴上有一对以上极点时，则要令Cs在虚轴极点附近所走的路径取半径为无穷小的半圆，使其绕过虚轴上的极点，CF曲线和系统开环幅相曲线的画法也要做相应的改变，然后就可以应用奈氏判据了。这里不再针对这种情况展开叙述。

【例5.5.2】若系统开环传递函数为

试用奈氏判据判别其闭环系统的稳定性。

【解】考虑到s→0时的情况，开环系统辐相曲线示于图5.5.10。从图5.5.10可知，N=-1，而由G（s）H（s）的表达式知P=0，根据奈氏判据有

所以系统不稳定。

【例5.5.3】若系统的开环传递函数为

试用奈氏判据判别其闭环系统的稳定性。

【解】考虑到s→0时的情况，开环系统辐相曲线示于图5.5.11。从图5.5.11可知，N=0，而由G（s）H（s）的表达式知P=0，根据奈氏判据有

图5.5.10　例5.5.2系统的开环奈氏曲线

图5.5.11　例5.5.3系统的开环奈氏曲线

所以系统稳定。