复变函数F（s）的选择及辐角原理解析

1.复变函数F（s）的选择

奈奎斯特稳定性判据是1932年奈奎斯特研究负反馈放大器时提出来的关于放大器的稳定性理论。后来，这个理论推广到自动控制中来，为频率响应法奠定了基础。

奈奎斯特稳定性判据的特点是根据开环系统频率特性来判别闭环系统的稳定性，也称为频域稳定性判据，简称奈氏判据。由于系统频率特性可用实验方法获得，因此对于难以用分析法求取数学模型的系统有更大的意义。

若系统结构图如图5.5.1所示，其开环传递函数为

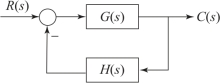
图5.5.1　系统结构图

式中 M1（s）——前向通路传递函数G（s）的分子关于s的多项式；

　　　N1（s）——前向通路传递函数G（s）的分母关于s的多项式；

　　　M2（s）——反馈通路传递函数H（s）的分子关于s的多项式；

　　　N2（s）——反馈通路传递函数H（s）的分母关于s的多项式；

　　　M（s）——系统开环传递函数分子关于s的多项式；

　　　N（s）——系统开环传递函数分母关于s的多项式。

系统闭环传递函数为

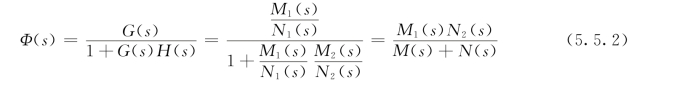
令复变函数

在实际系统中，开环传递函数分母N（s）的阶次n大于或等于其分子M（s）的阶次m，因而F（s）的分子和分母的阶次均等于n。这样可以把F（s）写成下面因子乘积的形式

式中，K为常数。比较式（5.5.2）、式（5.5.3）和式（5.5.4）可以看出，F（s）的零点zi为系统闭环传递函数Φ（s）的极点，F（s）的极点pj为开环传递函数G（s）H（s）的极点。由第3章时域分析知道，系统稳定的充分必要条件是系统闭环传递函数的全部极点均位于s平面的左半部。因此，闭环系统的稳定性仅由F（s）的零点zi在s平面的位置所决定。一般情况下，F（s）的零点并不知道，所以关键是找出确定F（s）的零点在右半s平面数目的方法，而这一方法可利用复变函数中的辐角原理得到。下面首先讲述辐角原理，然后在此基础上建立判别闭环系统稳定性的奈氏判据。

2.辐角原理

把式（5.5.4）两端写成模和辐角的指数形式，即

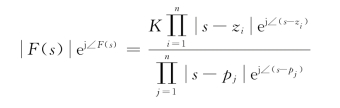
比较上式两端辐角，得

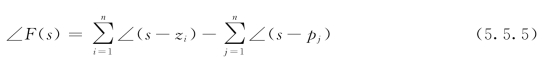(www.xing528.com)

s是复数，F（s）是复变函数，它们分别可用复数平面上的矢量来表示，其所对应的复数平面分别称为s平面和F平面，如图5.5.2（a）、（b）所示。在图5.5.2（a）中，s为矢量，s-zi和s-pj分别为由zi和pj指向A点的矢量，相应的函数F（s）为图5.5.2（b）中的矢量。

在s平面上过A点取某闭合路径Cs，若在Cs上不含有F（s）的零点zi和极点pj（i，j=1，2，…，n），并对于所有C上的s值，F（s）为单值有理函数，那么当s沿C顺时针移动一周时，矢量的辐角发生变化，则在图5.5.2（b）所示的F平面上表示F（s）的矢量辐角也相应变化，并形成一闭合路径CF。对上述过程，式（5.5.5）可写成下面增量形式，即

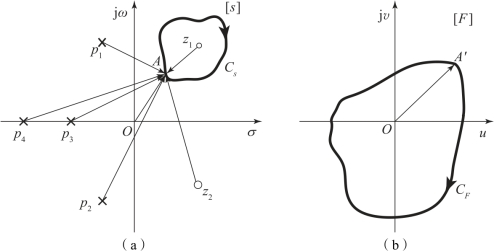
图5.5.2　s平面和F平面的映射关系示意图1

（a）s平面；（b）F平面

对于图5.5.2（a）而言，z1在Cs之内，而F（s）的其余零点和全部极点均在Cs之外。按照复变函数中矢量逆时针旋转角度为正的规定，则有

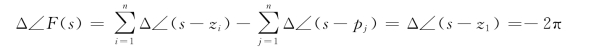
把上面的结果代入式（5.5.6），得所以，图5.5.2（b）的CF曲线围绕坐标原点顺时针旋转一周。

同理，若Cs为图5.5.3（a）所示路径，p1在Cs之内，而F（s）的其余极点和全部零点均在Cs之外，当s沿Cs顺时针移动一周时，则有

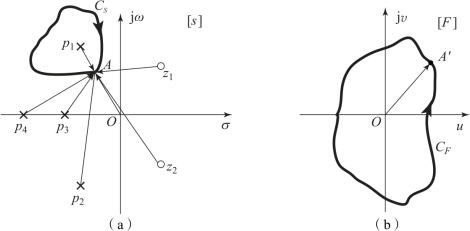
图5.5.3　s平面和F平面的映射关系示意图2

（a）s平面；（b）F平面

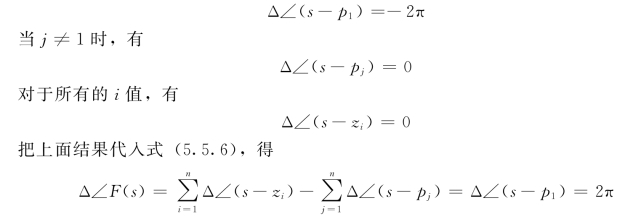
所以，图5.5.3（b）的CF曲线围绕坐标原点逆时针旋转一周。

一般情况下，若在Cs内含有F（s）的Z个零点和P个极点，当s沿Cs顺时针移动一周时，则有

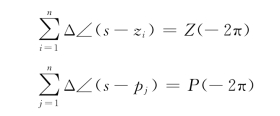
把上面的结果代入式（5.5.6），得

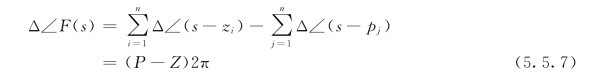
式（5.5.7）给出了一般情况下在闭合路径Cs内包含函数F（s）的零、极点数目，与当s沿Cs路径顺时针移动一周时F（s）的辐角增量之间的关系，这个关系式称为辐角原理。

根据辐角原理不难看出，如图5.5.4（a）所示的CF曲线顺时针包围坐标原点2周，即当s沿Cs路径顺时针移动一周时，Δ∠F（s）=2（-2π），则在s平面的Cs之内应包含2个F（s）的零点，或包含F（s）的零点zi的数目比包含F（s）的极点pj的数目多2个；图5.5.4（b）的情况相反，CF曲线逆时针包围坐标原点2周，即当s沿Cs路径顺时针移动一周时，Δ∠F（s）=2（2π），则在s平面的Cs之内应包含2个F（s）的极点，或包含F（s）的极点pj的数目比包含F（s）的零点zi的数目多2个；图5.5.4（c）所示的CF曲线没有包围坐标原点，即当s沿Cs路径顺时针移动一周时，Δ∠F（s）=0，则在s平面的Cs之内没有F（s）的零点和极点，或包含F（s）的零点zi和极点pj的数目相等。

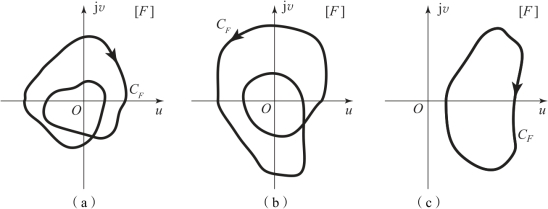
图5.5.4　CF曲线

（a）CF顺时针包围坐标原点2周；（b）CF逆时针包围坐标原点2周；（c）CF没有包围坐标原点