开环系统幅相频率特性曲线分析

根据系统开环频率特性的表达式，可以通过取点、计算和作图，绘制系统开环幅相频率特性曲线，本节主要结合工程需要，介绍绘制概略开环幅相频率特性曲线的方法。

1.确定开环幅相频率特性曲线的起点（ω=0+）和终点（ω=∞）

开环系统的一般频率特性表达式为（针对最小相位系统）

或

当n＞m时，有：

①当ν=0时，即零型系统，由式（5.4.1）、式（5.4.2）可知：

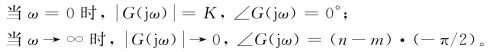
②当ν≠0时，即非零型系统，由式（5.4.1）、式（5.4.2）可知：

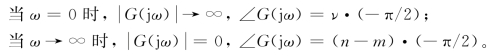
根据上面的结果，在图5.4.1（a）中示出ν=0、1、2时幅相曲线的大致形状及起点，图5.4.1（b）示出了其终点。

图5.4.1　开环幅相曲线的起点和终点示意图

（a）起点；（b）终点

但当开环系统频率特性中包含非最小相位环节时，上述结论不适用，这时需要根据开环系统中包含的各个典型环节，计算它们在起点（ω=0+）和终点（ω=∞）的相位，分别进行累加，以确定开环系统幅相曲线的起点和终点。

2.确定开环幅相频率特性曲线与实轴的交点

设ωx为开环幅相曲线与实轴相交时的频率，则G（jωx）的虚部为

或

而开环幅相频率特性曲线与实轴交点的坐标值为

3.确定开环幅相曲线的变化范围（象限、单调性）

【例5.4.1】某单位反馈系统的开环传递函数为

试概略绘制系统开环幅相频率特性曲线。

【解】由于惯性环节的角度变化为0°～-90°，故该系统开环幅相曲线的

起点：=K，φ（0）=0°；

终点：=0，φ（∞）=2×（-90°）=-180°。

系统开环频率特性

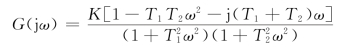
令Im[G（jωx）]=0，得ωx=0，即系统开环幅相曲线除在ω=0处外与实轴无交点。

由于惯性环节单调地从0°变化至-90°，故该系统幅相曲线的变化范围为第Ⅳ和第Ⅲ象限，系统概略开环幅相曲线如图5.4.2所示。(www.xing528.com)

【例5.4.2】设系统开环传递函数为

图5.4.2　例5.4.1系统的概略开环幅相曲线

试概略绘制系统开环幅相频率特性曲线。

【解】系统开环频率特性

由此作系统开环幅相曲线如图5.4.3中曲线①所示。图中虚线为开环幅相曲线的低频渐近线。由于开环幅相曲线用于系统分析时不需要准确知道渐近线的位置，故一般根据φ（0+）取渐近线为坐标轴，图中曲线②为相应的概略开环幅相曲线。

【例5.4.3】已知系统开环传递函数为

图5.4.3　例5.4.2系统的概略开环幅相曲线

试概略绘制系统开环幅相频率特性曲线。

【解】系统开环频率特性为

因为φ（ω）从-90°单调减至-270°，故幅相曲线在第Ⅲ与第Ⅱ象限间变化，概略开环幅相曲线如图5.4.4所示。

由以上例题可知，非最小相位环节的存在将对系统的频率特性产生一定的影响，在控制系统分析中必须加以重视。

【例5.4.4】系统的开环传递函数为

图5.4.4　例5.4.3系统的概略开环幅相曲线

试绘制系统的幅相频率特性曲线。

【解】延时环节的幅频特性为

相频特性为

其幅相曲线是以坐标原点为圆心、半径为1的圆。当系统存在延迟现象，即开环系统表现为延迟环节和线性环节的串联形式时，延迟环节对系统开环频率特性的影响是造成系统相位的明显滞后。

惯性环节G2（s）=的幅相曲线是以（5，j0）为圆心，半径为5的半圆。在半圆上任取频率点ω，设为A点，则G j（ω）的幅相曲线的对应点B位于以为半径，距A点圆心角θ=57.3×0.5ω的圆弧处，如图5.4.5所示。

图5.4.5　G（s）=e-0.5s的幅相曲线