使用频域实验确定系统传递函数

在分析和设计控制系统时，一般首先要确定被研究系统的数学模型。当难于用解析方法建立数学模型时，我们可以采用实验分析的方法来确定系统的数学模型。频域分析法的重要意义就在于它可以通过简单的频率响应实验，确定被控对象的传递函数。如果在感兴趣的频率范围内的足够多的频率点上测量出系统稳态输出与输入的幅值比和相位移，就可以据此绘出伯德图，然后利用渐近线可以确定出传递函数。

1.频率响应实验

频率响应实验原理如图5.3.15所示。首先选择信号源输出的正弦信号的幅值，以使系统处于非饱和状态。在一定频率范围内，改变输入正弦信号的频率，记录各频率点处系统输出信号的波形。由稳态段的输入、输出信号的幅值比和相位差，绘制对数频率特性曲线。

图5.3.15　频率响应实验原理

2.传递函数确定

从低频段起，将实验所得的对数幅频曲线用斜率为0 dB/dec、±20 dB/dec、±40 dB/dec等直线分段近似，获得对数幅频渐近特性曲线。由对数幅频渐近特性曲线就可以确定最小相位系统的传递函数，这是对数幅频渐近特性曲线绘制的逆问题。

【例5.3.4】若由频率响应实验获得某最小相位系统的渐近对数幅频特性曲线如图5.3.16所示，试确定其传递函数。

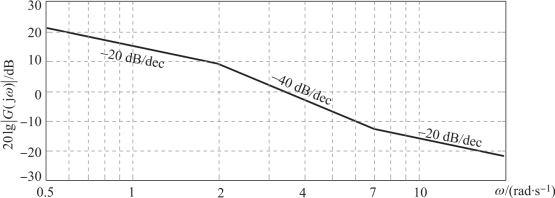
图5.3.16　例5.3.4的渐近对数幅频特性曲线

【解】

（1）由于对数幅频特性曲线最低频段的斜率为-20 dB/dec，所以系统有一个积分环节。

（2）在ω=1 rad/s处，L（ω）=15 dB，可求得K=5.6。

（3）在ω=2 rad/s处，渐近对数幅频特性曲线的斜率由-20 dB/dec变成-40 dB/dec，故系统有一个惯性环节，其时间常数T1=0.5 s。(www.xing528.com)

（4）在ω=7 rad/s处，渐近对数幅频特性曲线的斜率由-40 dB/dec变成-20 dB/dec，故系统有一个一阶微分环节，其时间常数T2=1/7=0.143 s。

根据上面的分析，得系统传递函数为

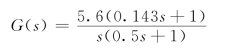
【例5.3.5】由频率响应实验获得某最小相位系统的渐近对数幅频特性曲线如图5.3.17所示，试确定其传递函数。

【解】根据图5.3.17可得系统传递函数为

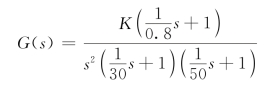
其对数幅频特性为

由图5.3.17可以看出，渐近对数幅频特性曲线在ω=4 rad/s通过横轴。考虑这一关系，由上式可得

由上式得K=3.2。

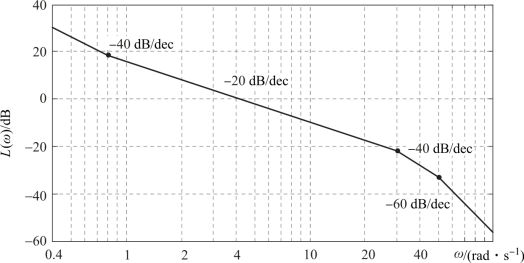
图5.3.17　例5.3.5系统的渐近对数幅频特性曲线

值得注意的是，实际系统并不都是最小相位系统，而最小相位系统可以和某些非最小相位系统具有相同的对数幅频特性曲线，因此还需依据相频特性来确定系统的传递函数。